


The outer disks of spiral galaxies and most dIrrs are dominated by gas in an atomic form, and not stars. Because stars form in molecular gas, it is difficult to observe directly how stars form in these regions. Moreover, outer disks and dIrrs tend to be stable by the Toomre Q condition (Elmegreen and Hunter 2015). Nevertheless, star formation usually looks normal there, forming clusters and associations at low density (Melena et al 2009, Hunter et al 2016a), although it may stop short of the full extent of the gas disk (see, for example, Fig. 2.)
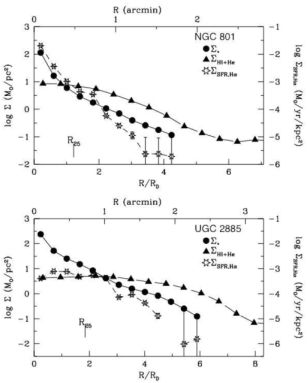 |
Figure 2. Stellar mass surface density Σ*, H i+He surface density ΣHI+He, and SFR density ΣSFR, Hα plotted as a function of radius for two very luminous (MV = −22 to −23) Sc-type spiral galaxies, NGC 801 and UGC 2885. The radius is normalized to the optical V-band disk scale length RD. The gas and stellar mass surface densities have been corrected to face-on. The logarithmic interval is the same for all three quantities, but the SFR zeropoint is different. Adapted from Hunter et al (2013). |
Krumholz (2013) formulated a model for star formation in these conditions that considers the existence of a two-phase atomic medium (i.e., a warm neutral medium in pressure equilibrium with a cool neutral medium) and the molecular fraction in such a medium. He then assumed that star formation occurs in the molecular medium at a rate given by an efficiency per unit free fall time, єff ∼ 0.01, times the molecular mass divided by the free fall time in the molecular gas:
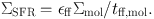 |
(1) |
The free fall time depends on the molecular cloud density, which for outer disks in their model, depends on the molecular cloud mass and a fiducial value of the molecular cloud surface density, ΣGMC = 85 M⊙ pc−2. The molecular cloud mass was taken to be the turbulent Jeans mass in the interstellar medium (ISM), MGMC = σ4 / (GΣgas) for turbulent speed σ and average ISM gas surface density Σgas. For inner disks, the free fall time was taken to be the value for an average disk density where the Toomre Q parameter equals unity. To span the inner and outer regions, the minimum of these two free fall times was used.
One uncertainty in the Krumholz (2013) model is the assumption that a two-phase medium is present, because it need not be present everywhere in the outer disk. But this assumption seems reasonable for star formation because cool gas greatly facilitates cloud formation (Elmegreen and Parravano 1994, Schaye 2004, Forbes et al 2016). A second assumption is that the SFR is given only by the molecular gas mass and density, and that this is related to the total density by the molecular fraction, which depends on the ratio of the radiation field to the cool cloud density. In this model, molecule formation is calculated separately as a precursor to star formation, and then whatever is calculated for molecules is used to determine the SFR.
Another model considers that the average SFR is determined by the average ISM dynamics and that molecule formation is incidental, i.e., molecule formation happens along the way but it is not a limiting factor. Star formation in predominantly atomic gas has been predicted by Glover and Clark (2012) and Krumholz (2012) and suggested by observations in Michałowski et al (2015) and Elmegreen et al (2016). In this model, the gas mass available for star formation is the total gas mass in all forms, even atomic gas, and the free fall rate of this gas is given by the average midplane density, regardless of molecular content (Elmegreen 2015). Cool clouds are still required so the ISM cannot be purely warm phase. Also, because molecular hydrogen is slow to form at low density (Mac Low and Glover 2012), there could be a substantial fraction of H2 in stagnant, diffuse clouds without significant CO emission and with little connection to star formation (Elmegreen and Hunter 2015). Such a diffuse H2 medium was found in simulations by Hu et al (2016) and Safranek-Shrader et al (2016) but has not been observed yet. These diffuse H2 clouds, along with more atom-rich clouds, would presumably come together during localized ISM collapse as a precursor to star formation. In this model the SFR per unit area is given by
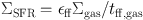 |
(2) |
for midplane free-fall time tff at the density ρ = Σgas / (2H) and scale height H = σ2 / ( π G Σgas). The result is (Elmegreen 2015)
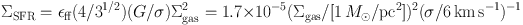 |
(3) |
where σ is the gas velocity dispersion and єff ∼ 1% is the efficiency of star formation per unit free fall time.
Both of the above models compare well with observations (Krumholz 2013, Elmegreen 2015).
Hu et al (2016) simulated dwarf galaxies with a chemical model to form H2, CO and other molecules, cloud self-shielding from radiation, and a SFR given by Eq. (2) at a threshold density of 100 cm−3 and a temperature less than 100 K. They found that ΣSFR decreases faster than Σgas but not because of a flare (the extra Σgas factor in Eq. 3). Rather, ΣSFR follows the cold gas with a rate that scales directly with the cold gas fraction, i.e., a linear law, and this cold gas fraction decreases with radius. The linear law in their model is because of the assumed constant threshold density. Most star-forming gas is close to this fixed density, so the characteristic dynamical time is the fixed value at this density.
This point about a fixed density is similar to the explanation for the linear star formation law in Elmegreen (2015), where it was pointed out that if CO, HCN, and other star formation tracers emit mostly at their fixed excitation density, as determined by the Einstein A coefficient, then the effective free fall time is the fixed value at this density. The SFR then scales only with the amount of gas at or above this observationally selected density. The fixed density in this case is not because of an assumption about a star formation threshold, as there is no threshold in the Elmegreen (2015) model. There is just a continuous collapse of ISM gas at a rate given by the midplane density, and a feedback return of the dense gas to a low density form.
The existence of a fixed threshold density for star formation is something to be tested observationally. Elmegreen (2015) suggest there is no threshold density because clouds are strongly self gravitating when π GΣcloud2 > PISM for cloud surface density Σcloud and ambient pressure P. Because the interstellar pressure varies with the square of the total surface density of gas and stars inside the gas layer, there is a large range in pressure over several exponential scale lengths in a galaxy disk—a range that may exceed a factor of 100 for dIrrs, and 1000 for spirals. Thus if there is a threshold for star formation, the above equation suggests that it might be
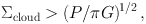 |
(4) |
in which case it should vary with radius.
We return to a point made in Sect. 1 about the gas surface density profile in the far-outer regions of gas-rich galaxies. Wang et al (2014) noted that the gas exponential scale length beyond the radius R1, where Σgas = 1 M⊙ pc−2, is always about 0.25 times this radius. We can see this here also from Eq. (3), which states that
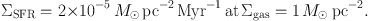 |
(5) |
After a Hubble Time of 104 Myr, Σstars is approximately 0.2 M⊙ pc−2. According to the average disk mass profiles in Zheng et al (2015), this outer stellar surface density is lower than that at the disk centre by 10−3.5 on average, which represents eight scale lengths in stars. But eight scale lengths in stars is four scale lengths in gas for Eq. (3). Thus the radius at 1 M⊙ pc−1 is about four times the scale length in the gas, as observed further out by Wang et al (2014).