Annu. Rev. Astron. Astrophys. 2017. 55: 59-109 Copyright © 2017 by Annual Reviews. All rights reserved

2. AB INITIO SIMULATIONS OF GALAXY FORMATION

2.1. Star formation and gas cooling

Most modern cosmological galaxy formation simulations allow for metal enrichment and metal dependent radiation equilibrium cooling (for specific implementations see e.g. Kravtsov 2003, Scannapieco et al. 2005, Oppenheimer & Davé 2006, Tornatore et al. 2007, Wiersma, Schaye & Smith 2009, Ceverino & Klypin 2009, Vogelsberger et al. 2013) of gas in the presence of the UV/X-ray background radiation from quasars and galaxies (e.g. Faucher-Giguère et al. 2009, Haardt & Madau 2012). If the gas is cooling rapidly, or in the presence of a rapidly changing radiation field, non-equilibrium cooling will be more accurate (see e.g. Gnat & Sternberg 2007, Oppenheimer & Schaye 2013a) and first steps in this direction have been made in galaxy scale simulations (Oppenheimer & Schaye 2013b, Richings, Schaye & Oppenheimer 2014, Hu et al. 2016, Richings & Schaye 2016, Forbes et al. 2016, Oppenheimer et al. 2016). Out of the cool gas reservoir the formation of the stellar populations is modeled in a simplified way as the relevant spatial and temporal scales as well as the complex ISM physics cannot be resolved in a cosmological context.

Cosmological simulations typically treat star formation in a Schmidt-type manner (Schmidt 1959) relating the local star formation rate density to the gas density divided by a time-scale. This time-scale depends on local gas properties like the dynamical and/or gas cooling time as introduced by Katz (1992) and Cen & Ostriker (1992b). Some implementations couple the star formation rate to molecular gas properties inspired by observed connections (Wong & Blitz 2002, Kennicutt et al. 2007, Leroy et al. 2008, Bigiel et al. 2008, Kennicutt & Evans 2012) and use a constant time-scale in combination with the variable local H₂ fraction (e.g. Pelupessy, Papadopoulos & van der Werf 2006, Robertson & Kravtsov 2008, Gnedin, Tassis & Kravtsov 2009, Monaco et al. 2012, Christensen et al. 2012, Feldmann, Gnedin & Kravtsov 2012, Kuhlen et al. 2012) which is, however, itself connected to the H₂ formation time-scale. It should be noted that H₂ based star formation models in galaxy simulations add another level of complexity and uncertainty. The small-scale structure of the ISM, the detailed radiation field, ionization degrees, magnetic field strengths, all relevant for H₂ formation (e.g. Glover & Mac Low 2007, Hennebelle & Iffrig 2014, Walch et al. 2015), are unresolved in most galaxy scale and all cosmological simulations (see, however, Hopkins, Quataert & Murray 2012b) and it is unclear whether H₂ formation is the primary driver for star formation (see e.g. Glover & Clark 2012, Krumholz 2013).

The star formation models typically require a normalization, the star formation efficiency, as well as a parameter determining the scaling with gas density. The parameters are adjusted to match the zero point and the slope of the observed Kennicutt-Schmidt relation between star formation rate surface density and gas surface density (Kennicutt 1998). The basic implementations have been extended by sub-resolution models to capture some characteristics of the multi-phase structure of the gas (e.g. Springel & Hernquist 2003). An alternative implementation for star formation is based on gas pressure (see e.g. Schaye & Dalla Vecchia 2008, Schaye et al. 2015) assuming that galatic disks are in approximate vertical pressure equilibrium. Such a model has been shown to be in good agreement with the observed Kennicutt-Schmidt relation with no need for additional calibration (Schaye & Dalla Vecchia 2008). If used in combination with a fixed equation of state for the star forming gas the behaviour is similar to a density dependent criterion as the relation of gas pressure and density is fixed. In general, only gas below a certain temperature and above a certain density, which can be metal dependent, is eligible for star formation (see Hopkins, Narayanan & Murray 2013 for a discussion of star formation criteria). Also in large scale cosmological simulations these parameters must be calibrated as the ISM is in general unresolved and gas cooling is effectively not followed below a few thousand Kelvin (Schaye et al. 2015, Vogelsberger et al. 2014, Khandai et al. 2015).

2.2. The formation of disk dominated systems

Even though the formation of Milky Way systems has turned out to be the more difficult problem, it was historically the first one tackled. Can we make the Milky Way from reasonable cosmological initial conditions applying the relevant physical processes? Simulators typically have used the 'zoom technique' (Navarro & White 1994) wherein a representative region of the Universe is simulated first with a dark matter only code, and then a relevant high density piece is re-simulated with a hydro-dynamical code with allowance for the gravitational forces and gas inflow due to the surrounding matter.

In hierarchical cosmological models for the formation of galaxies, small structures form first, grow, and merge into larger objects. In this framework, galaxies form through the cooling of gas at the centers of dark matter halos, where it condenses into stars (White & Rees 1978). To match the observed properties of galaxies and galaxy clusters, purely gravitational processes on their own cannot account for cosmological structure formation, but gas cooling/dissipation processes must be considered (Silk 1977, Rees & Ostriker 1977, Binney 1977). These three very early papers already presented the physical arguments for the observed scales of galaxies noted in our first paragraph. It had been realized early-on from analytical estimates that the conservation of angular momentum of the cooling gas within dark matter halos could lead to the formation of galactic disks with flat rotation curves (Fall & Efstathiou 1980). In early work (White & Rees 1978) it was already noted that at high-redshift gas has to be prevented from excessive cooling into overly dense regions - possibly by feedback from massive stars to avoid the overproduction of condensed baryonic matter (Larson 1974, Dekel & Silk 1986, Navarro & Benz 1991). Also, to produce dynamically cold and thin stellar, extended disks, the accretion of high angular momentum gas from outer regions of the halos is needed in the more recent past (Fall 1979). This would require feedback processes to eject gas and avoid early over-efficient star formation at high redshift as well as the formation of gas reservoirs to allow the gas to return at low redshifts with higher angular momentum.

Early cosmological simulations including the dissipative gas component (but neglecting star formation) confirmed the problem (Navarro & Benz 1991, Katz & Gunn 1991, Navarro & White 1994). Too many baryons settled into disks which were much more compact than observed spiral galaxies with too high rotation velocities due to substantial angular momentum loss during the assembly process caused by mergers. Not only was the angular momentum for the forming gaseous disks too low, but also too many baryons would be locked up in galaxies (Navarro, Frenk & White 1995, Navarro & Steinmetz 1997).

The over-cooling problem was confirmed by many studies that followed (see e.g. Balogh et al. 2001). Once a stellar component was included in the simulation it was possible to approximately treat the feedback from young stellar populations. In addition to radiative cooling the role of energy injection by supernovae could be tested. Investigators quickly discovered that, while the detailed implementation can change the results significantly (e.g. Navarro & White 1993, Sommer-Larsen, Gelato & Vedel 1999, Thacker & Couchman 2000, Robertson et al. 2004, Okamoto et al. 2005) almost all cosmological simulations resulted in the overproduction of stars, in low angular momentum bulges (e.g. Katz, Weinberg & Hernquist 1996, Balogh et al. 2001, Kereš et al. 2005). It was again suggested that the origin of the problem lies at higher redshift (van den Bosch et al. 2002, D'Onghia & Burkert 2004). Galaxies would be less concentrated and have higher specific angular momentum if gas cooling were suppressed before the host halo has assembled (Weil, Eke & Efstathiou 1998). Still, simulations experimenting with thermal and kinetic energy injection (e.g. Abadi et al. 2003a and many that followed) resulted in similar problems, with the conclusion that the assumed feedback models were insufficient to prevent the early collapse of low angular momentum baryons and their conversion into stars, a problem that remained unsolved for a long time.

Thus, the early attempts at ab initio cosmological computations failed or only partially succeeded to make disk systems that were as low mass and extended in space and time of formation as those in the real Universe (Abadi et al. 2003a, b, Robertson et al. 2004, 2006a Governato et al. 2004, Scannapieco et al. 2009, Piontek & Steinmetz 2011, Agertz, Teyssier & Moore 2011). It is important to recall that observations had shown (see Section 1.1) that real, forming galaxies were embedded in strong gaseous outflows that were missing from the simulations.

Recently, a number of groups have made significant progress on reducing the galaxy fraction, f_gal, in halos of ∼ 10¹² M_⊙ and at the same time forming spiral galaxies with more realistic properties. In Fig. 2 we show examples from six groups who recently succeeded in producing disks with spiral like morphologies but very different simulation codes. These studies utilize a variety of qualitatively different sub-resolution approaches to the response of the high-density star forming gas on newly formed and dying stellar populations. All these 'successful' approaches have in common that gas in dense star forming regions can efficiently be pushed out in a galactic outflow and, possibly, escape from the galaxies and their dark matter halos. With outflow launching, Milky Way like halos develop disk-like galaxies. Detailed investigations of gas flows in the forming galaxies - which are most easily followed in Lagrangian SPH simulations (see also Genel et al. 2013, Nelson et al. 2015, 2016) - have revealed most characteristics and consequences of galactic outflows. With strong stellar feedback, a significant fraction of the low angular momentum gas cooling to the centers of dark matter halos at high redshift is prevented from being converted into stars and can be blown out of the galaxies. When the proto-galaxies are still small and have shallow potential wells, this gas will leave the galaxies and never return or can return at much later times with angular momentum enhanced by non-linear gravitational torques or mixing (e.g. Marinacci et al. 2011) with the rotating halo gas (Brook et al. 2011, Übler et al. 2014). The outflow supresses the formation of stellar bulges from the low angular momentum gas at high redshift and enriches the circum-galactic medium with metals (Governato et al. 2010, Brook et al. 2012, Marinacci et al. 2014, Christensen et al. 2016). It also reduces the previously reported dramatic effects of mergers. The gas still looses angular momentum but a significant fraction can be ejected before stars are formed. This is particularly efficient if the mergers happen early in smaller proto-galaxies (Übler et al. 2014).

Figure 2. Recent cosmological zoom simulations with strong stellar feedback of galaxies with sprial like morphologies. The pictures show mock images of the stellar light. Top left: SPH (GASOLINE) simulation of Stinson et al. (2013) including dust attenuation. Top middle: Moving-mesh (AREPO) simulation of Marinacci, Pakmor & Springel (2014). Top right: SPH (GASOLINE) simulation of Guedes et al. (2011). Bottom left: SPH (GASOLINE) simulation of Hopkins et al. (2014). Only the face-on view includes dust attenuation. Bottom middle: SPH (GADGET) simulation of Aumer et al. (2013). Bottom right: AMR (RAMSES) simulation of Agertz & Kravtsov (2015). Only the face-on view includes dust attenuation.

Contrary to what has been believed for a long time, even galaxies with early major mergers can evolve into present day disk-like galaxies with low bulge fractions (Springel & Hernquist 2005, Robertson et al. 2006a, Aumer, White & Naab 2014). For more massive systems the enriched gas is kept within the halo (in a galactic fountain) and is accreted back onto the galaxy later on with metallicity enhanced, sometimes repeatedly (Oppenheimer & Davé 2008, Oppenheimer et al. 2010, Pilkington et al. 2012, Brook et al. 2014, Genel et al. 2015). This process reduces star formation and delays the onset of galaxy formation in halos of all masses, in much better agreement with high redshift abundance matching constraints (e.g. Stinson et al. 2013, Hirschmann et al. 2013, Hopkins et al. 2014). The late accretion of gas with high angular momentum from outside the halo is increased as fewer baryons were converted into stars in accreted structures. This is pretty much as it was predicted 38 years ago (Fall 1979).

In addition, at low redshift a moderately constant gas accretion rate onto spiral galaxies can be sustained by enriched gas that has been cycling within the halo of the galaxy (Oppenheimer et al. 2010, Übler et al. 2014, Christensen et al. 2016). Therefore gas accretion onto the galaxy is decoupled from the halo assembly, resulting in flatter star formation histories more consistent with observations (Hirschmann et al. 2013, Stinson et al. 2013, Hopkins et al. 2014, Woods et al. 2014). In Fig. 3 we show two recent examples of the generic effect of strong feedback on galactic star formation rate histories. Additionally, Milky Way progenitor galaxies are larger (with strong feedback models) already at high redshift and the overall cosmological evolution in size is significantly reduced (Hirschmann et al. 2013, Aumer, White & Naab 2014) in much better agreement with observations. The above results rely on 'recipes' to treat physical processes that are relevant below the resolution scale of the simulations and sometimes even impact the simulation in well resolved regions. The variety of these models is remarkable and a good understanding of the strengths and weaknesses of these models is relevant to assess whether scientific progress has been made or whether the good agreement with observations is the result of an empirical matching exercise. In the following we review the general pathways followed by different groups.

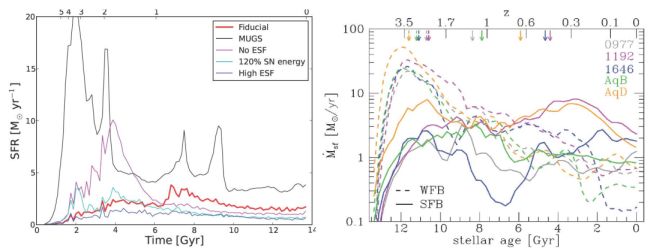Figure 3. The effect of stellar feedback on the star formation histories of simulated disk galaxies. Stronger feedback results in the suppression of early star formation, relatively flat star formation histories and, in the cases shown here, disk like morphologies. The flatter star formation rate histories but not the disk-like morphologies are generic for all simulations with strong feedback. Flat star formation histories are in better agreement with observations of Milky Way-sized spiral galaxies. Left panel: The simulations presented in Stinson et al. (2013) show peaked star formation histories for simulations with weak feedback (MUGS Stinson et al. 2010), No ESF). Star formation at high redshift is suppressed for models with strong feedback (Fiducial, 120% SN energy, High ESF). Right panel: The same trend is seen in a comparison of five galaxies simulated with weak (dashed lines, Oser et al. 2010) and strong feedback (solid lines, Aumer et al. 2013). The stellar half-mass formation times (arrows) are shifted from z ∼ 2 to z ≲ 1 (Übler et al. 2014).

2.2.1. Current sub-resolution models for feedback from stellar populations   Feedback from massive stars has long been suggested to resolve the over-cooling problem in galaxy formation and various different sub-resolution feedback models have been presented to approximate the complex physical processes. Here we call a sub-resolution model an empirical, physically motivated numerical recipe representing the large scale impact of energy, mass and momentum during the life and death of massive stars in state of the art cosmological simulations of large volumes. These models are necessary as the finest resolution elements (in large scale cosmological simulations) are typically a few hundred parsecs which makes it impossible for these simulations to capture the small-scale multi-phase structure of the galactic ISM. In Section 3.1 we will demonstrate why these models can only be a crude representation of reality, limiting the predictive power of present day galaxy formation simulations.

One class of models might be termed 'delayed cooling' models (Gerritsen 1997, Thacker & Couchman 2000). In one incarnation of this approach (Stinson et al. 2006) the energy from supernova explosions is injected into neighboring gas but the cooling is 'turned off' for gas inside the expected Sedov blast wave radius (McKee & Ostriker 1977). This way gas can efficiently be heated and accelerated. Although often being criticized as being unphysical due to the suppression of gas cooling, the model attempts to allow for formation of super-bubbles (e.g. Mac Low & McCray 1988, see Keller, Wadsley & Couchman 2015 for a modern implementation of superbubble formation in cosmological simulations and Section 3.1). The 'delayed cooling' model significantly reduces the galaxy stellar masses and promotes the formation of disk dominated systems (Governato et al. 2007, Guedes et al. 2011, Keller, Wadsley & Couchman 2016). The models have been extended, in a simplified way, by taking into account the additional energy release from massive stars before they explode as supernova (Stinson et al. 2013, Kannan et al. 2014, Wang et al. 2015). It has been pointed out by Rosdahl et al. (2016) that the delayed cooling approach results in a significant amount of thermally unstable circumgalctic gas, which can be problematic when estimating the gas emission and absorption in galactic halos.

A related approach is 'stochastic thermal' feedback (Dalla Vecchia & Schaye 2012), which does not suffer from some of the problems of the 'delayed cooling' approach (see e.g. Rosdahl et al. 2016). Here the mean thermal energy injection per unit formed stellar mass is fixed and neighboring star particles are, stochastically, only heated if their temperature can be moved above a certain temperature threshold (e.g. ≳ 10^7.5 K). This guarantees long cooling times, the onset of a Sedov phase and efficient momentum generation similar to the 'delayed cooling' models. The total energy injection is an adjustable parameter and can slighly exceed the available supernova energy (Crain et al. 2015, Schaye et al. 2015) compensating for the artificial overcooling. However, the model has been demonstrated to drive strong winds (Dalla Vecchia & Schaye 2012). It has been used for one of the most successful cosmological galaxy formation simulation suite (the Eagle simulations, Schaye et al. 2015) in terms of matching observed galaxy population properties and their evolution with redshift (Schaye et al. 2015, Furlong et al. 2015, Rahmati et al. 2015, Bahé et al. 2016).

The gas cooling is also delayed in 'non-thermal' heating models (Teyssier et al. 2013). Here the energy is injected into a non-thermal energy component, representing turbulence, magnetic fields or cosmic rays, with a dissipation time-scale of ∼ 10 Myr. The energy injection procedure follows the 'stochastic thermal' heating (e.g. Roškar et al. 2014).

A 'two phase' approach is followed in Scannapieco et al. (2006) where the hot and the cold gas phase are evolved separately using SPH (Marri & White 2003). The supernova energy added to a cold gas particle is stored (i.e. decoupled from the hydrodynamics) and only released when it can become a constituent of the hot phase. Accounting for the momentum input by supernovae and (potential) radiation pressure in a simplified way this model also produces spiral galaxies with realistic properties (see Fig. 2, Aumer et al. 2013).

Another popular approach might be termed 'wind feedback'. Some fraction of the energy released by massive stars is injected into the surrounding gas in the form of energy or momentum by which it is driven away from the region of star formation. The wind is parameterized by a mass loading factor η, i.e. the ratio of wind mass-loss to the star formation rate and by a wind velocity v_wind. The original implementation assumed a constant mass loading and a fixed wind velocity coupled to a stiff effective equation of state for the gas resulting from thermal energy input from supernovae (Springel & Hernquist 2003). Here the gas in the wind is decoupled from the hydodynamical calculations when leaving the star forming reagions with its given velocity and is later (the conditions depend on the respective implementations) incorporated in the calculations again (see also Vogelsberger et al. 2014). Observations and theoretical considerations, however, indicate decreasing mass-loading and increasing wind velocities in higher-mass galaxies with higher star formation rates (Martin 2005, Murray, Quataert & Thompson 2005). This motivated Oppenheimer & Davé (2006, 2008) to introduce a momentum driven wind model. The wind velocity scales with the velocity dispersion of stars in the galaxies (or the dark matter, Vogelsberger et al. 2013) v_wind ∝ σ, the momentum input scales with the star formation rate, _wind × v_wind ∝ _*, and the mass loading is inversely proportional to the velocity dispersion η ∝ dm_wind / dm_* ∝ 1 / v_wind ∝ 1 / σ_*. Again, to ensure that the gas leaves the star-forming regions it is then decoupled and later re-incorporated in regions with lower gas density.

Although this model has become popular, some authors (Schaye et al. 2010) turned off the 'wind decoupling' the consequences of which are discussed in Dalla Vecchia & Schaye (2008). Although empirical in nature, the galactic wind models results in realistic (compared to observations) enrichment histories of galaxies and the circum-galactic medium (Finlator & Davé 2008, Davé, Finlator & Oppenheimer 2011), lower conversion efficiencies in particular in the regime of disk galaxies (Sales et al. 2010, Puchwein & Springel 2013), reasonable abundances and flatter star formation histories for low mass galaxies and higher gas fraction for star forming galaxies at high redshift (Oppenheimer & Davé 2008, Davé, Finlator & Oppenheimer 2011, Hirschmann et al. 2013) and a more realistic cosmic star formation history (Schaye et al. 2010). Although originally developed for SPH simulations, decoupled 'momentum driven' winds have also been used in recent moving mesh simulations with wind velocities scaled to the local dark matter velocity dispersions (e.g. the Illustris simulation, Vogelsberger et al. 2014). With cosmological zoom simulations it has been demonstrated that realistic present day spiral galaxies (Marinacci, Pakmor & Springel 2014, Grand et al. 2016) as well as gas rich massive high-redshift disks (Genel et al. 2012, Anglés-Alcázar et al. 2014) can be formed with a momentum driven wind model in which 'decoupling' has been applied.

Alternatively, an energy driven wind model has been proposed (Okamoto et al. 2010) to explain the low abundance of satellite galaxies in the Milky Way. Here the wind velocity also is assumed to scale with the velocity dispersion v_wind ∝ σ, the energy input scales with the star formation rate, _wind × v_wind² ∝ _*, and the mass loading is taken to be inversely proportional to the square of the stellar velocity dispersion η ∝ dm_wind / dm_* ∝ 1 / v_wind² ∝ 1 / σ². This model results in the same wind speeds but higher mass-loading for lower mass galaxies and better agreement for the Milky Way satellites luminosity function (Okamoto et al. 2010). In a hybrid model Davé et al. (2013) combine a momentum driven wind scaling with the energy driven wind scaling for galaxies below σ = 75 km s⁻¹ to obtain a better match to the galaxy mass function at low masses (see also Barai et al. 2013 for a 'radially varying wind model'). This transition was motivated by the idea that low mass galaxies are more affected by supernova explosions whereas the effect of radiation pressure takes over at higher masses (Murray, Quataert & Thompson 2005, 2010). In an updated incarnation of the 'decoupled' wind model Davé, Thompson & Hopkins (2016) have used scaling from high-resolution cosmological zoom simulations (Muratov et al. 2015) to set the mass-loading and wind velocities. Efforts are underway to replace these heuristic methods with others based more closely on high-resolution multi-phase physical modeling.

2.3. The formation of bulge dominated systems

Spheroidal early-type galaxies have been 'easier' to simulate from straightforward cosmological initial conditions (any cosmological simulation with weak feedback will result in the overproduction of spheroidal galaxies). The escape velocities are larger for these more massive systems and so the energy input from feedback matters somewhat less, and, while still important, stellar feedback appears to be less critical to the formation process. Empirically they are known to form in dense regions starting at early times and the observed structures of proto-ellipticals are quite small as seen at redshift z = 2-3 (see Section 1.3). Thus, the difficulties encountered in making disk-like systems - too early star formation in too concentrated systems - are alleviated for the construction of physically plausible spheroidal systems. As a consequence, cosmological simulations with weak stellar feedback and without AGN feedback have effectively been used as reasonable initial models for the formation of massive, early type galaxies. In these simulations the final galaxies follow observed early-type galaxy scaling relations of size and velocity dispersion with stellar mass (Naab et al. 2007, Oser et al. 2010, Feldmann et al. 2010, Johansson, Naab & Ostriker 2012, Feldmann, Carollo & Mayer 2011). They also have plausible stellar populations with metallicity distributions that are modulated by their merger history (Kobayashi 2004, 2005). However, compared to observations based on abundance matching constraints, their stellar masses are about a factor of 2 - 4 too high at a given halo mass (Oser et al. 2010). This has been presumably due to the lack of sufficient energy input (see e.g. Meza et al. 2003, Croton et al. 2006), and it was alleviated as AGN feedback simulations have been improved.

For high halo masses, the evolution of the galaxies shows a clear two-phase characteristic (Naab et al. 2007, Oser et al. 2010, Feldmann et al. 2010, Johansson, Naab & Ostriker 2012, Navarro-González et al. 2013, Rodriguez-Gomez et al. 2016, Qu et al. 2017). At early times (z ≳ 1.5) the galaxies grow by in-situ star formation in the deep potential wells of massive halos. As the low angular momentum gas is efficiently converted into stars, some of the systems can be remarkably small (also supported by mergers, Wuyts et al. 2010, Bournaud et al. 2011a), very similar to the population of observed high-redshift compact galaxies (Sommer-Larsen & Toft 2010, Oser et al. 2010, 2012, Wellons et al. 2016). Towards lower redshifts in-situ star formation becomes less important as cold gas can no longer easily penetrate the shocked hot gaseous halos (e.g. Birnboim & Dekel 2003) and the mass assembly becomes dominated by the accretion of stars that have formed in other galaxies. Cosmological simulations clearly indicate that stellar accretion is more important at higher galaxy masses (Oser et al. 2010, Lackner et al. 2012, Gabor & Davé 2012, Rodriguez-Gomez et al. 2016, Qu et al. 2017). This robust trend is also found in abundance matching estimates (Section 1.6) and semi-analytical galaxy formation models (Khochfar & Silk 2006, Guo & White 2008) and it is strongest for central galaxies in galaxy clusters (Ostriker & Hausman 1977, De Lucia & Blaizot 2007). The late, collisionless assembly has important consequences for the structural evolution of the system. As a significant fraction of mass can be accreted in mergers with smaller and less bound systems (Gabor & Davé 2012, Lackner et al. 2012), this stellar mass is added to the systems at large radii (Oser et al. 2010, Navarro-González et al. 2013, Rodriguez-Gomez et al. 2016, Qu et al. 2017). The resulting strong increase in galaxy size is driven by accreted stars. Simple arguments based on the virial theorem (Naab, Johansson & Ostriker 2009, Bezanson et al. 2009) show that the same mass added in many minor mergers will produce a much more extended galaxy than if that mass had been added in fewer, more major mergers (Eq. 1, Section 1.5) . Together with the weak decrease in velocity dispersion the evolution of the individual model galaxies is consistent with observational estimates.

The low present day star formation rates and spheroidal shapes of galaxies simulated with weak stellar feedback are primarily caused by the efficient early gas depletion and early conversion of gas into stars in combination with efficient shock heating of the halo gas and gravitational heating caused by the accretion of smaller systems (Johansson, Naab & Ostriker 2009, Khochfar & Ostriker 2008). Still, the weak feedback models provide an attractive start for the physical solution of the observed structural evolution of massive galaxies (see also Feldmann, Carollo & Mayer 2011, Feldmann & Mayer 2014). In its extreme limit the assembly of brightest cluster galaxies and the size evolution of cluster galaxies can be well explained in a substantially collisionless cosmological assembly model assuming that all stars in cluster progenitor galaxies have formed before z ∼ 2 (Laporte et al. 2013).

With simulations neglecting AGN feedback it has been shown that the formation history of massive galaxies leaves its imprint on the gas and stellar kinematic properties of present day early-type galaxies (Naab et al. 2014, Wu et al. 2014, Serra et al. 2014). Epochs dominated by gas dissipation will result in the formation of flattened stellar distributions (disks), supported by rotation. Major mergers are rare, and during minor merger dominated phases the stellar systems experience stripping and violent relaxation, existing cold gas may be driven to the central regions causing starbursts, trigger the formation and growth of super-massive black holes or be expelled from the systems in galactic winds. This, in turn, will impact the distribution of cold gas and the kinematics of stars forming thereof. With improved cosmological simulations we move towards a better understanding of the angular momentum evolution of galaxies (see Genel et al. 2015, Zavala et al. 2016). In a first step, using cosmological zoom simulations Naab et al. (2014) have been able to demonstrate that gas dissipation and merging result in observable features (at present day) in the two-dimensional kinematic properties of galaxies, which are clear signatures of distinct formation processes.

Many of these features are in agreement with all the valuable predictions from isolated merger simulations (see Section 1.5). Dissipation favors the formation of fast rotating systems and line-of-sight velocity distributions with steep leading wings, a property that can be directly traced back to the orbital composition of the systems (Röttgers, Naab & Oser 2014, see also Bryan et al. 2012 for the obital distribution of dark matter). Merging and accretion can result in fast or slowly rotating systems with counter-rotating cores, cold nuclear or extended (sometimes counter-rotating) disks showing dumbbell-like features all observed in real galaxies and in part well understood from binary merger experiments.

We have seen that models with stronger feedback and metal cooling, applied to cosmological simulations, delay the onset of star formation in more massive halos and the systems become more gas rich at high redshift, a trend that continues towards low redshift. This makes galaxies too massive with too high star formation rates in particular at the central regions (e.g. Kravtsov & Borgani 2012). This had also been found prior to cosmological simulations (e.g. Ciotti et al. 1991, Ciotti & Ostriker 1997), due simply to the inevitable cooling flows occurring in massive systems. One dimensional and two dimensional high resolution simulations of the effect of AGN feedback (Binney & Tabor 1995, Ciotti & Ostriker 2001, Sazonov et al. 2005, Novak, Ostriker & Ciotti 2011) indicated that AGN feedback alleviates this problem. With ab inito cosmological simulations a number of groups have now demonstrated that 'feedback' from an accreting supermassive black hole can suppress the residual star formation in the central regions of massive galaxies, confirming the proposal put forward by (Silk & Rees 1998). In the following we review some sub-resoluton approaches for implementing feedback from supermassive black holes.

2.3.1. Current models for feedback from super-massive black holes   Several different models have been proposed to approximate the effect of AGN feedback and to follow it in cosmological simulations. In most galaxy scale sub-resolution models (starting from Springel, Di Matteo & Hernquist 2005b) the accretion rate onto the black hole _BH is computed based on the Bondi-Hoyle-Lyttleton formula (actually invented for spherical accretion of interstellar gas onto the Sun, (Hoyle & Lyttleton 1939, Bondi & Hoyle 1944, Bondi 1952)

(2)

Here c_s is the sound speed of the surrounding gas and v_rel is the relative velocity of the black hole and the gas (see Rosas-Guevara et al. 2015 for modifications of the Bondi rate due to an assumed viscous accretion disk, see also Hopkins et al. 2016 for the possible failure of Bondi accretion in high-resolution simulations). Also included in many models is an adjustable accretion 'boost factor' α_boost which can have values up to 100 in some implementations. The general motivation for using a boost factor is the low resolution of the simulations which are unable to follow the accurate multi-phase gas structure near the black holes and therefore the accretion rates (see discussion in Booth & Schaye 2009). In fact many implementations use Bondi accretion in combination with a stiff equation of state for the high density gas resulting in gas with increasing temperature at higher densities - contrary to the expected structure in the dense ISM (McCarthy et al. 2010, Puchwein & Springel 2013, Vogelsberger et al. 2013, 2014, Hirschmann et al. 2014, Khandai et al. 2015, Schaye et al. 2015). As a result the sound speed becomes artificially high and a high α_boost compensates for this. From a practical, not physical, point of view the boost factor ensures that enough gas is accreted to grow super-massive black holes of reasonable masses. As in Springel, Di Matteo & Hernquist (2005b), the accretion in most models is limited by the Eddington rate. In some recent implementations (see, however, Pelupessy, Di Matteo & Ciardi 2007) the relative velocity between the black hole and the ambient medium is not considered (the Lyttleton part) as the black holes are continuously centered to the potential minimum of the host halo (e.g. Puchwein & Springel 2013, Vogelsberger et al. 2014). Choi et al. (2012) take an alternate approach that does not have a boost factor; they stochastically treat the overlap of the smoothing sphere and the Bondi sphere, thereby statistically allowing for the resolution limits. Also Schaye et al. (2015) have eliminated the boost factor and regulate the Bondi rate with the ratio of the Bondi to viscous time-scale (Rosas-Guevara et al. 2015). Still, the same limitations apply for the temperature and density structure of the nuclear gas.

It has been proposed by Shlosman, Frank & Begelman (1989) that black holes might be primarily fed by gas driven to the center by gravitational torques from non-axisymmetric perturbations (see also e.g. Gabor & Bournaud 2013, Bournaud et al. 2011b, Hopkins & Quataert 2011). Hopkins & Quataert (2011) argue that 'torque limited' accretion behaves qualitatively different to other accretion models and produces reasonable scaling relations with a smaller scatter. The parametrized version of this accretion model is a bit more complicated and less straigh forward to be included in larger scale cosmological simulations, but the first attempts are promising (Anglés-Alcázar, Özel & Davé 2013, Anglés-Alcázar et al. 2016). Clearly the choice between the two approaches should be driven by the ratio of the amnount of angular momentum in the gas to be accreted with the 'torque limited' model when the ratio of the centrifugal radius to the Bondi radius becomes larger than unity.

Approaches following the traditional feedback models assume that some fraction (є_therm ∼ 0.05) of the bolometric luminosity L_bol = є_r dM_BH / dt c² (Shakura & Sunyaev 1973, Soltan 1982), with c being the speed of light and a radiative efficiency of є_r = 0.1 (Shakura & Sunyaev 1973), is converted into and deposited as thermal energy in the surrounding ISM such that the energy injection rate is dE_therm / dt = є_therm є_{r BH} c². Sijacki et al. (2007) proposed a 'jet bubble' modification to this simple model depending on the gas accretion rate onto the black hole. For accretion rates above 1% of the Eddington rate the usual fraction of є_therm є_r of the accreted rest mass energy is deposited as thermal energy to the surrounding medium. For lower accretion rates the feedback efficiency is increased from 0.5% to 2% of the rest mass energy and is injected into heated off-center bubbles that can then buoyantly rise (see Fabjan et al. 2010, Hirschmann et al. 2014, and Vogelsberger et al. 2014 for slightly modified versions). Such models are designed to mimic the observed jet induced bubble formation (Fabian et al. 2006, Fabian 2012) and, due to the enhanced coupling efficiency at low accretion rates, i.e. low black hole growth rates (see e.g. Churazov et al. 2005, Merloni & Heinz 2008), it helps to prevent the formation of cooling flows and nuclear star formation in massive halos (Sijacki et al. 2007). Dubois et al. (2012), in a RAMSES implementation, also identify a 'radio mode' at low accretion rates and inject kinetic energy into a jet-like bipolar outflow with a velocity of 10,000 km s⁻¹ (see also Omma et al. 2004 and Brighenti & Mathews 2006 for the impact of jet feedback in isolated models).

Originally developed for SPH, the Sijacki et al. (2007) AGN feedback model has also been used in recent large scale simulations with the moving mesh code AREPO extended by the influence of the radiation field of the accreting black holes on the cooling rate of the gas (Sijacki et al. 2015, Vogelsberger et al. 2014). Here the effect of AGN feedback on reducing the galactic stellar masses was confirmed, however, at the cost of depleting the massive halos of gas due to the 'jet bubble' feedback, inconsistent with observations (Genel et al. 2014). In general, these relatively straight forward models not only give reasonable galaxy and black hole masses at the high mass end, they also result in plausible evolutions of the black hole populations and AGN luminosity functions across cosmic time (Puchwein & Springel 2013, Hirschmann et al. 2014, Sijacki et al. 2015, Khandai et al. 2015).

Instead of using a constant boost factor, Booth & Schaye (2009) scale α_boost with the local density for high ambient gas densities and set it to unity for low densities - in combination with a stiff equation of state for dense gas (Schaye & Dalla Vecchia 2008, see Booth & Schaye 2009 for a detailed disucssion). The thermal feedback is regulated such that the black hole stores the energy until the surrounding particles can be heated to a certain high temperature (in this case ≳ 10⁸ K), disfavoring rapid cooling of the gas and making the immediate feedback efficient by construction. The approach is similar to the stellar 'stochastic thermal' feedback discussed in Section 2.2.1. It is clear that the density scaling of α_boost makes the accretion more sensitive to the feedback, which in turn strongly affects the density. In general, however, the introduction of a temperature limit for the black hole feedback results in a stronger effect than for the Springel, Di Matteo & Hernquist (2005b) model with no need for changing the energy conversion efficiency and the feedback methodology. This model also results in reasonable baryon fractions and stellar masses for massive galaxies and black hole masses (Schaye et al. 2015). In particular it reproduces reasonable gas fractions and X-ray luminosities for galaxy groups (McCarthy et al. 2010, Le Brun et al. 2014, Choi et al. 2014) which are over-predicted by models with a constant boost factor and thermal feedback.

An Eddington limited thermal black hole feedback scheme similar to Booth & Schaye (2009) with a density dependent α_boost and the same underlying equation of state for the gas, has also been implemented in the adaptive mesh refinement code RAMSES (Teyssier et al. 2011, Dubois et al. 2012). The black holes are not seeded in halos above a certain mass but the accreting sink particles are generated when certain conditions on the stellar component and gas density are met (Teyssier et al. 2011, see e.g. Dubois et al. 2012, Di Matteo et al. 2012, Puchwein & Springel 2013, Hirschmann et al. 2014 for different implementations of black hole seeding).

Zoom simulations of group and cluster sized halos in particular have highlighted the impact of AGN feedback on reducing the stellar mass in the central galaxies by preventing cooling flows and subsequent star formation (Sijacki et al. 2007, Teyssier, Chapon & Bournaud 2010, McCarthy et al. 2010). AGN feedback also has important consequences for the hot gas in these halos. By removing low entropy gas at higher redshifts (at the peak of the black hole growth) AGN bring the simulated present day hot gas properties in much better agreement with observations of thermal X-ray emission (McCarthy et al. 2010, McCarthy et al. 2011, Le Brun et al. 2014).

The above simulations also indicate a potentially interesting effect of AGN feedback on the stellar kinematics. As the amount of gas cooling and subsequent star formation in the central galaxies is efficiently suppressed (Martizzi, Teyssier & Moore 2012, Martizzi et al. 2012), the ratio of in-situ formed to accreted stars is significantly reduced, increasing the size of the system but also reducing the amount of rotational support (Dubois et al. 2013a, Martizzi et al. 2014). AGN feedback transforms BCGs from fast rotators to slow rotators, possibly in better agreement with observations (Dubois et al. 2013b, Martizzi et al. 2014). This highlights the potentially important role of AGN feedback for regulating the ratio of in-situ star formation to accretion (Hirschmann et al. 2012, Dubois et al. 2013b) determining the stellar kinematics of the systems and regulating the stellar density distributions.

The strength of these kinematic signatures will not only be influenced by feedback from AGN and stars, but also by the mass of the galaxies and their environment. Low mass, star forming disk galaxies favored in low-density environments, predominantly grow by accretion of gas and subsequent in-situ star formation, and are affected by stellar feedback, and less so by AGN. Higher mass, early-type galaxies form in high-density environments - primarily affected by feedback from accreting super-massive black holes - and their late assembly involves merging with other galaxies, which might also be of an early type (e.g. Rodriguez-Gomez et al. 2016, Qu et al. 2017). So far it has not been possible to perform a statistically meaningful comparison of kinematic properties of galaxy populations to observed population properties, like the observed increasing fraction of slow versus fast rotators for early-type galaxies as a function of environmental density (Cappellari 2011). With the newly performed Eagle (Schaye et al. 2015) and Illustris (Vogelsberger et al. 2014) simulations this might now be possible for the first time, due to the large simulated volume and the relatively high spatial resolution attained (≲ 1kpc). Not only can the simulated two-dimensional kinematic properties be compared to observations, it will also be possible to make (statistical) connections to characteristic formation histories, properties of progenitor galaxy populations and to investigate trends with environment. This will not only be limited to stellar kinematics but will also include gas kinematics and metallicity and two-dimensional stellar abundance patterns. In addition, we will be able to assess the impact of the major feedback mechanisms (from massive stars and AGN) on the kinematic properties of high and low mass galaxies in all environments, a study that will be supported by higher resolution, cosmological zoom simulations for characteristic cases. Also several recent papers (e.g. Crain et al. 2010, Bogdán et al. 2013, Le Brun et al. 2014, Choi et al. 2014, Le Brun et al. 2014, Le Brun, McCarthy & Melin 2015) have shown that a proper prediction of the thermal X-ray halos of massive galaxies provides a stringent test of the correctness of any implemented feedback scheme. We discuss mechanical and radiative AGN feedback models in Sec. 3.5.