Copyright © 2011 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2011. 49:409-470
Copyright © 2011 by Annual Reviews. All rights reserved |
The past decade has seen marked improvements in the data and analysis techniques employed in cluster cosmology. Chandra observations of relaxed clusters provided important measurements of the distance scale, confirming the recent acceleration of the cosmic expansion. Improvements in mass measurements led to a convergence in estimates of σ8 from cluster counts, and X-ray surveys extending to z ≳ 0.5 provided the first constraints on dark energy from the growth of structure. We begin this section with a review of the latest results from measurements of the number and growth of clusters, as well as the closely related problem of constraining scaling relations. We then review the state of other cluster-based probes of cosmology. We conclude by summarizing the latest constraints on dark energy from the combination of galaxy cluster data with other, independent probes. The application of cluster measurements to other areas of fundamental physics are discussed in Section 5.
Because the cosmological model influences predictions for scaling relation observations, and vice versa (Section 2.5.1), the two must be constrained simultaneously. The statistical framework needed for this approach, in which a subset of detected clusters are targeted for more detailed observations including mass estimation, is described by Mantz et al. (2010b). Without reproducing the details here, we enumerate the components of the statistical model:
Using the likelihood function corresponding to this formalism (see Mantz et al. 2010b), constraints on cosmological and scaling relation parameters are obtained by marginalizing over the true, unknowable properties of each cluster, constrained by the measured values. Straightforward adaptations of this approach, for example incorporating a cluster bias model (Section 2.2.1) or stacked gravitational lensing data for poor clusters and groups, are possible.
4.1.2. LOCAL ABUNDANCE AND EVOLUTION
We concentrate our review on three recent, independent results based on measurements of the local abundance and evolution of clusters from X-ray and optical surveys, as well as preliminary results from new SZ surveys.
Mantz et al. (2008; 2010b) studied the BCS (Ebeling et al. 1998), REFLEX (Böhringer et al. 2004) and Bright MACS (Böhringer et al. 2004) cluster samples compiled from the RASS. This survey strategy, covering a large fraction of the sky to relatively shallow depth, is optimized to the task of finding the largest clusters at the expense of depth in redshift. The Mantz et al. data set consists of 238 clusters with masses M500 > 2.7 × 1014 M⊙ distributed over the redshift range 0 < z < 0.5. Pointed Chandra or ROSAT follow-up observations were used to measure Mgas for 94 clusters, while the remaining 144 had measurements only of the cluster redshift and survey flux. The Mgas – Mtot relation was marginalized over using hydrostatic mass estimates for relaxed clusters from Allen et al. (2008). The data set was used to simultaneously constrain cosmological parameters and the LX – M and TX – M relations using the method described above and detailed in Mantz et al. (2010b).
Vikhlinin et al. (2009b) also used X-ray selected clusters, but pursued a different survey strategy. Their data set consists of disjoint low-redshift and high-redshift samples, with 49 clusters (originally culled from several RASS samples) at redshifts 0.025 < z < 0.22 (nearly all < 0.1) and an additional 36 clusters serendipitously detected in the 400 Square Degree Survey (Burenin et al. 2007) at 0.35 < z < 0.9. This survey strategy, covering a smaller area of the sky to greater depth, naturally finds fewer of the most massive clusters, but extends to lower masses (M500 > 1.3× 1014 M⊙) and higher redshifts. All 85 clusters in the full data set were followed up with Chandra, and their masses were estimated using either Mgas or YX as a proxy; the proxy–mass relations were calibrated using hydrostatic mass estimates for a sample of well observed, low-redshift clusters. The analysis includes empirical constraints on the scaling relations and corrections for selection effects, though not using exactly the approach described in Section 4.1.1.
The top panels of Figure 9 provide a simplified visualization of how constraints on dark energy arise from these data, comparing the observed mass function in two redshift ranges to model predictions for different cosmological models. In particular, an open universe with no dark energy clearly under-predicts the evolution of the mass function over the redshift range of the data.
 |
Figure 9. Examples of cluster data used in recent cosmological work. Top: Measured mass functions of clusters at low and high redshifts are compared with predictions of a flat, ΛCDM model and an open model without dark energy (from Vikhlinin et al. 2009b). Bottom: fgas(z) measurements for relaxed clusters are compared for a Ωm = 0.3, ΩΛ = 0.7, h = 0.7 model (left, consistent with the expectation of no evolution) and a Ωm = 1.0, ΩΛ = 0.0, h = 0.5 model (right; from Allen et al. 2008). For purposes of illustration, cosmology-dependent derived quantities are shown (mass and fgas); in practice, model predictions are compared with cosmology-independent measurements. |
The optically selected maxBCG sample (Koester et al. 2007) employed by Rozo et al. 2010 probes a different part of the cluster population; it is restricted to lower redshifts than the X-ray samples described above (0.1 < z < 0.3), but extends to lower masses (M500 > 7 × 1013 M⊙). This lower effective mass limit, which changes less strongly with redshift compared to X-ray surveys, makes the maxBCG sample significantly larger than the others, with > 104 clusters divided into 9 bins based on optical richness. Mean masses for 5 richness ranges were estimated through a weak gravitational lensing analysis of stacked clusters, providing information from which to constrain the richness–mass relation. The cosmological analysis accounts for the covariance between cluster counts in each richness bin and the mean lensing mass estimates.
The results obtained by these three groups on flat ΛCDM and constant w models are summarized in Table 2. Note that, for the two works which fit w models, the results on Ωm and σ8 are dominated by the low-redshift data and so are not degraded noticeably by the introduction of w as a free parameter; thus all three sets of constraints are directly comparable. The agreement between the different works, as well as others listed in Table 2, is encouraging; in particular, the close agreement in the constraints on σ8 reflects the relatively recent convergence in cluster mass estimates using different techniques, and our improved understanding of the relevant systematics (Section 3.3; see also, e.g., Henry et al. 2009). Importantly, the concordance ΛCDM model provides an acceptable fit to the data in each case.
| Reference c | Data | σ8 | Ωm | ΩDE | w | h |
| Local abundance and evolution d | ||||||
| M10 | X-ray | 0.82 ± 0.05 | 0.23 ± 0.04 | 1−Ωm | −1.01 ± 0.20 | |
| V09 | X-ray | 0.81 ± 0.04 | 0.26 ± 0.08 | 1−Ωm | −1.14 ± 0.21 | |
| Local abundance only | ||||||
| R10 | optical | 0.80 ± 0.07 | 0.28 ± 0.07 | 1−Ωm | −1 | |
| H09 | X-ray | 0.88 ± 0.04 | 0.3 | 1−Ωm | −1 | |
| Local abundance and clustering | ||||||
| S03 | X-ray | 0.71−0.16+0.13 | 0.34−0.08+0.09 | 1−Ωm | −1 | |
| Gas-mass fraction | ||||||
| A08 | X-ray | 0.27 ± 0.06 | 0.86 ± 0.19 | −1 | ||
| A08 | X-ray | 0.28 ± 0.06 | 1−Ωm | −1.14−0.35+0.27 | ||
| E09 | X-ray | 0.32 ± 0.05 | 1−Ωm | −1.1−0.6+0.7 | ||
| L06 | X-ray+SZ | 0.40−0.20+0.28 | 1−Ωm | −1 | ||
| XSZ distances | ||||||
| B06 | X-ray+SZ | 0.3 | 1−Ωm | −1 | 0.77−0.09+0.11 | |
| S04 | X-ray+SZ | 0.3 | 1−Ωm | −1 | 0.69 ± 0.08 | |
| a Entries ΩDE = 1 −
Ωm indicate the assumption of
global spatial flatness (or use of WMAP priors requiring flatness
at the few percent level); other entries without error bars indicate
parameters that were fixed in the corresponding analysis.
b Error bars are marginalized (single-parameter) 68.3% confidence intervals, and include each author's estimate of the systematic uncertainties (with the exception of S04). c A08 = Allen et al. (2008); B06 = Bonamente et al. (2006); E09 = Ettori et al. (2009); H09 = Henry et al. (2009); L06 = LaRoque et al. (2006)<; M10 = Mantz et al. (2010b); R10 = Rozo et al. (2010); S03 = Schuecker et al. (2003); S04 = Schmidt, Allen & Fabian (2004); V09 = Vikhlinin et al. (2009b). d Cluster surveys extending to redshifts z ≳ 0.3 are required to constrain w from the evolution of the mass function. Note that the Ωm and σ8 constraints from these works are essentially unchanged, whether or not w is allowed to differ from −1. |
||||||
Figure 10 (left panel) shows the joint constraints on Ωm and σ8 obtained by Rozo et al. (2010) [solid lines], which display the typical degeneracy between those parameters from cluster survey data. (The degeneracy can be broken, for example, by including cluster fgas data; see Section 4.2.) Also shown are results from 5 years of WMAP data (Dunkley et al. 2009) [dashed lines], which are tight for the assumed flat ΛCDM model. Nevertheless, it is evident that the combination of the two types of data (shaded regions) is significantly improved over either one individually.
 |
Figure 10. Left: Joint 68.3% and 95.4% confidence regions for the mean matter density and perturbation amplitude from the abundance of clusters in the maxBCG sample (z < 0.3) compared with those from WMAP data (Dunkley et al. 2009) for spatially flat ΛCDM models. The shaded region indicates the combination of the two data sets. From Rozo et al. (2010). Right: Constraints on the dark energy density and equation of state from the abundance and growth of clusters in the 400 Square Degree sample (z < 0.9) compared with those from WMAP, SNIa (Davis et al. 2007) and BAO (Eisenstein et al. 2005; Percival et al. 2007) for spatially flat, constant w models. Note that, contrary to the convention followed in the other figures, the shaded regions in the right panel indicate only 39.3% confidence. The tight contraints from WMAP compared with Figure 11 result from the fact that a simplified analysis was used, in particular neglecting the influence of dark energy on the Integrated Sachs-Wolfe effect (e.g. Spergel et al. 2007). From Vikhlinin et al. (2009b). |
The constraints on constant w models from Vikhlinin et al. (2009b) and Mantz et al. (2010b) are respectively shown in Figures 10 (right panel) and 11, along with results from various other cosmological data sets. The cluster results are in good agreement with one another, as well as with the other, independent data. The ∼ 20% precision constraint on w from cluster growth alone (including systematic uncertainties) is clearly competitive, and further constraining power may be available from theoretical advances (see Section 4.5). The strong degeneracy in CMB constraints evident in Figure 11 also arises in many other models that are more complex than flat ΛCDM; the ability of cluster data to break this degeneracy by providing precise and independent constraints on σ8 (right panel of Figure 11) makes the combination particularly powerful (e.g. Section 5.3).
 |
Figure 11. Joint 68.3% and 95.4% confidence regions for the dark energy equation of state and mean matter density (left) or perturbation amplitude (right) from the abundance and growth of RASS clusters at z < 0.5 (labeled XLF; Mantz et al. 2010b) and fgas measurements at z < 1.1 (Allen et al. 2008), compared with those from WMAP (Dunkley et al. 2009), SNIa (Kowalski et al. 2008) and BAO (Percival et al. 2010) for spatially flat, constant w models. Combined results from RASS clusters and WMAP are shown in gray in the right panel; gold contours in both panels show the combination of all data sets. The BAO-only constraint differs from that in Figure 10 due to the use of different priors. Adapted from Mantz et al. 2010b [the BAO constraints in the left panel have been updated to reflect more recent data]. |
Although their respective surveys are not yet complete, preliminary results have been reported from SZ-detected clusters from the South Pole Telescope (SPT; Vanderlinde et al. 2010) and Atacama Cosmology Telescope (ACT; Sehgal et al. 2011). As the number of cluster detections used in these works is small, respectively 21 and 9 at redshifts 0.16 < z < 1.2, the data are not capable of producing interesting constraints on their own, but both groups demonstrate consistency with results from the WMAP satellite (Komatsu et al. 2011). Neither group has yet obtained simultaneous constraints on cosmology and the relevant SZ scaling relation, making their final error budgets strongly dependent on the priors chosen to constrain the scaling relation.
To obtain scaling relations appropriate for constraining cosmology, the analysis of the two must be simultaneous and must account properly for the influence of the survey selection function (e.g. Stanek et al. 2006 and Sahlén et al. 2009) and the cluster mass function, as in Mantz et al. (2010a) (see also Sections 4.1.1 and Section 2.5.1). Some authors have included corrections for the expected Malmquist bias given a flux limit or selection function (Pacaud et al. 2007; Pratt et al. 2009; Vikhlinin et al. 2009a), but most analyses of scaling relations in the literature employs least-squares regression without detailed consideration of sample selection. Since various cluster samples, with different selection functions, have been used, it is not surprising that results on the slopes, scatters and evolution of the scaling relations have varied widely compared with the formal uncertainties. Another statistical issue is that the covariance that comes about when the scaling quantities are measured from the same observations, for example temperature and hydrostatic masses from X-ray data, is commonly ignored (see Section 7).
The method used to estimate masses has also varied. Most authors have used the assumption of hydrostatic equilibrium applied to X-ray data, regardless of the dynamical state of the cluster, which must introduce spurious scatter due to departures from equilibrium and non-thermal support (e.g. Nagai, Vikhlinin & Kravtsov 2007). More recently, mass proxies such as gas mass (e.g. Mantz et al. 2010a) and X-ray thermal energy (YX; e.g. Maughan 2007; Pratt et al. 2009; Vikhlinin et al. 2009a; Andersson et al. 2010), or gravitational lensing signal (e.g. Hoekstra 200; Johnston et al. 2007; Rykoff et al. 2008; Leauthaud et al. 2010; Okabe et al. 2010) have been employed.
These variations in mass estimation and analysis methods, in addition to changes to instrument calibration over the years, makes a comprehensive and fair census of scaling relation results problematic. Here we focus on the cosmological importance of scaling relation measurements, citing examples from recent work where the issues mentioned above are at least partially mitigated.
For X-ray and SZ observables, under the assumption of strict self-similarity (no additional heating or cooling), Kaiser (1986) derived specific slopes and redshift dependences for the power-law form of Equation 16:
 |
(24) |
where the factors of E(z) = H(z) / H0 are appropriate for measurements made at a fixed critical-overdensity radius. The subscripts ‘bol’ and ‘mw’ reflect the fact that these predictions apply to the bolometric luminosity and mass-weighted temperature. Optical richness is more complex to predict, but empirical studies that map galaxies to sub-halos in simulations support a power law richness–mass relation for groups and clusters (Conroy & Wechsler, 2009).
Figures 12 and 13 show a few examples of recent scaling relation measurements. Leauthaud et al. (2010) present a M – LX relation for X-ray selected clusters in the COSMOS field by measuring stacked weak lensing masses (left panel of Figure 12). Under the common assumption of symmetric scatter in the log, stacking on LX allows the mean M(LX) relation to be recovered, at the cost of losing information about the intrinsic scatter. As the authors note, transforming these results to an LX(M) relation introduces a dependence on the mass function. Stacked lensing was also used to determine the mass–richness relation of optically selected clusters in SDSS by Johnston et al. (2007). Their results are shown in the right panel of Figure 12; red points in the figure show that compatible masses were derived from galaxy velocity dispersion measurements.
 |
Figure 12. Scaling relations using masses from stacked weak lensing observations. The vertical axes show mean mass derived from stacking clusters in each bin. Left: X-ray selected clusters from the COSMOS field binned in luminosity (from Leauthaud et al. 2010, see references therein for other data sets plotted). The gray band corresponds to a 68% confidence predictive region from a fit to the COSMOS data (brown squares). Right: Optically selected clusters from SDSS (a subset of the maxBCG catalog) binned in richness. Black points are masses from weak lensing, while red points show mass determinations from galaxy velocity dispersion measurements for the same clusters (Becker et al. 2007). From Johnston et al. (2007). |
For more massive systems, lensing can provide mass estimates on a cluster-by-cluster basis. The left panel of Figure 13 shows such a mass–temperature relation from Hoekstra (2007) for X-ray selected clusters. Since temperature only weakly influences X-ray detectability, selection bias should be relatively unimportant here, although intrinsic correlation with luminosity can still produces subtle biases relative to a mass-limited sample (Section 2.5.1).
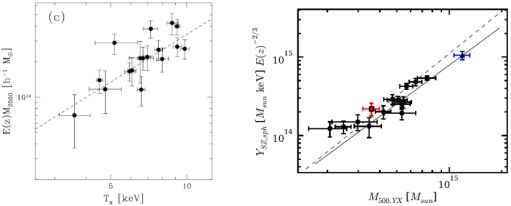 |
Figure 13. Scaling relations using masses estimated for individual clusters. Left: weak lensing masses versus ICM temperature for an X-ray selected sample imaged by the Canada–France–Hawaii Telescope. From Hoekstra (2007). Right: spherically-integrated SZ signal (Y) versus mass for SPT-detected clusters, where masses are estimated using X-ray thermal energy (YX) from Chandra observations as a proxy. Y is measured from the SPT survey data. The solid line is a fit to the data, while the dashed line shows a prediction based on the results of Arnaud et al. (2010). From Andersson et al. (2010). |
An SZ scaling relation from Andersson et al. (2010), using clusters detected by SPT, appears in the right panel of Figure 13; in this case, masses are estimated from measurements of the X-ray thermal energy, YX, and an assumed YX – M relation. This case is instructive in that the plotted Y values are derived from the survey data, with suggestions of Malmquist bias in the flattening observed at the lowest masses (compare with Figure 5; this potential bias is accounted for in the fit in Figure 13).
Recently, the Planck Collaboration released an early SZ-selected cluster catalog together with an analysis of SZ scalings for existing X-ray and optical cluster samples (Planck Collaboration 2011a and references therein). Measurements of the scaled SZ signal from Planck as a function of X-ray luminosity for ∼1600 X-ray selected galaxy clusters are shown in the left panel of Figure 14, along with the stacked, mean SZ signal in luminosity bins and model expectations derived from the observed X-ray properties (Planck Collaboration 2011c). There is good agreement between the model expectations and the Planck observations, validating the simple model description of the hot ICM over the mass and redshift range probed.
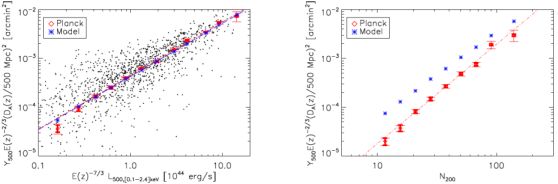 |
Figure 14. Recent SZ scaling relations from Planck. Left: scaled, intrinsic SZ signal vs. X-ray luminosity for a sample of X-ray selected clusters, with SZ extraction radii determined from LX (see Planck Collaboration 2011c for details). Red diamonds show the LX-stacked relation, while the blue asterisks show the predicted SZ signal based on X-ray scaling relations. For these clusters, the agreement of the model with measurements is good. Right: Scaled, stacked SZ signal vs. optical richness for optically selected maxBCG clusters (red diamonds) are compared to expectations based on the maxBCG mass–richness relation in combination with X-ray scaling relations (blue asterisks, see Planck Collaboration 2011b for details). The origin of the offset between the predictions and measurements is not yet understood. |
The right panel of Figure 14 shows the result of a similar exercise, stacking the Planck SZ signal as a function of richness for the optically selected maxBCG catalog. Also shown is the expected signal, based on the observed mean mass–richness relation for the maxBCG sample (Rozo et al. 2009) and a standard X-ray Y – M scaling relation (Planck Collaboration 2011b). In this case, the observed Planck SZ signal lies well below model predictions. For an X-ray detected sub-sample of the maxBCG catalog, however, relatively good agreement between the Planck SZ measurements and model predictions is observed (Planck Collaboration 2011b).
An important difference between the LX and richness comparisons is that the centers and radii used to extract the clusters' SZ signals from the (relatively low resolution) Planck data were respectively based on X-ray and optical estimates. Besides optical center and scale mis-estimates, other potential sources for the discrepancy in Figure 14b include lower than expected purity in the optical sample (with lower mass halos being enhanced in richness by projection); unmodeled biases in the scaling relations used (e.g. the impact of non-thermal pressure support on the X-ray relations); and the presence of an intrinsic anti-correlation between the galactic and hot gas mass fractions in the clusters. These and other possibilities are under investigation.
In general, most current scaling results are consistent with power-law relations over a wide range in mass (e.g. Sun et al. 2009; Rozo et al. 2010). However, the exponents often differ from the values in Equation 24, due at least in part to the impact of astrophysical processes, mainly star/SMBH formation and associated feedback, discussed in Section 2.1.2. For example, the LX – M slope is commonly found to exceed 4/3, with the value depending on the mass range explored. There is less consensus on the TX – M slope, with most estimates consistent with self-similarity (e.g. Henry et al. 2009; mt = 0.65 ± 0.03), but some finding a shallower slope (e.g. Mantz et al. 2010a; mt = 0.48 ± 0.04); systematics related to correlated observables, mass estimation (see Section 7), instrument calibration, selection, and differences in the mass range studied may play a role. There are fewer empirical estimates of the Y – M or YX – M slopes, but most are broadly compatible with the predicted value. We note that departure from self-similar scaling with mass does not necessarily imply departure from self-similar evolution with redshift; for example, the high-mass halos in the preheated simulations of Stanek et al. (2010) have X-ray luminosities that evolve within 10% of the self-similar expectation at z ≤ 1, despite having a slope with mass that is 50% steeper than self-similar.
The marginal intrinsic scatter in each relation determines the degree of selection bias in surveys and each observable’s usefulness as a mass proxy; current results are reviewed in Section 3.3.4.
The evolution of the scaling relations is of great importance, since it is potentially degenerate with the cosmological signal of cluster growth. Because the impact of survey limits can vary strongly with redshift for X-ray surveys, it is particularly crucial to account for them in this context. Both Vikhlinin et al. (2009a) and Mantz et al. (2010a) investigate evolution in the LX – M relation, finding only marginal ∼ 1σ departures from the self-similar redshift dependence in Equation 24. Mantz et al. (2010a) additionally found no evidence for departures from self-similar evolution in the TX – M or center-excised LX – M relations (see Section 6.4). As current and upcoming surveys expand the reach of cluster samples to z > 1, obtaining precise constraints on scaling relation evolution will be imperative (see also Section 7).
The effects of survey bias on scaling relations can be partially mitigated by selecting clusters based on an observable other than the observable of immediate interest (e.g. Rykoff et al. 2008). However, as Sections 2.4.1 and 2.5.1 make clear, the amount of residual bias depends on the intrinsic correlation between the two observables at fixed mass. To date, the only empirical estimates of such correlation are for mass and X-ray luminosity at fixed optical richness, r(LX, M|Ngal) ≥ 0.85 (Rozo et al. 2009); and for soft-band X-ray luminosity and temperature at fixed mass, r(LX, TX|M) = 0.09 ± 0.19 (Mantz et al. 2010a). Large, overlapping surveys, and/or surveys coupled with multi-wavelength follow-up campaigns, are required to better constrain the property covariance of clusters; ultimately, such constraints will provide a new level of robustness to cosmological work.
4.1.4. MOST MASSIVE CLUSTER TESTS
In principle, the confirmed existence of even a single galaxy cluster of implausibly high mass would challenge the standard ΛCDM model with Gaussian initial conditions. Recently, the discovery of high redshift, massive systems such as XMMU J2235.3-2557 at z ∼ 1.4 (Mullis et al. 2005; Rosati et al. 2009) and SPT-CL J0546-5345 at z ∼ 1.1. Brodwin et al. (2010) have led to reports of possible tension with Gaussian ΛCDM (Jee et al. 2009; Holz & Perlmutter 2010; Hoyle, Jimenez & Verde 2010).
Such a test is in some sense an attractively simple alternative to the more involved work discussed above. However, despite the fact that the test involves only one or a few very massive clusters detected in a survey rather than the complete sample, a robust assessment of the likelihood still requires a detailed understanding of the selection function and survey biases, as well as a full accounting for the effects of scatter in the mass–observable scaling relations (Sections 2.5.1 and 4.1.1). The accuracy and precision of the cluster mass measurements are also critical, due to the steepness of the high mass tail of the cluster mass function. Errors in mass measurements at the tens of per cent level, for example (as might be expected for weak lensing measurements of an individual cluster), can modify the likelihood of such a cluster being observed by up to an order of magnitude.
Mortonson, Hu & Huterer (2011) estimate confidence limits for the exclusion of the Gaussian ΛCDM model based on the properties of the most massive galaxy cluster, or N most massive galaxy clusters, detected in a given survey, employing constraints on the expansion history from current data. These authors conclude that none of the presently known high mass, high redshift clusters are in significant tension with the standard Gaussian ΛCDM paradigm.
The framework described in Section 4.1.1 for simultaneously constraining cosmology and scaling relations has yet to be applied to the spatial clustering of clusters. However, Schuecker et al. (2002) have obtained cosmological constraints using a method based on the Karhunen-Loève eigenvectors of 428 clusters from the X-ray selected REFLEX sample above a luminosity of 5.1 × 1042h70−2 ergs−1 (see Vogeley & Szalay 1996 for the theory underlying this method of estimating the power spectrum). The constraints are relatively weak compared with more recent results from other methods: 0.6 < σ8 < 2.6 and 0.07 < Ωm < 0.38 at 95.4% confidence, fixing h = 0.7 and without including the systematic uncertainty due to cosmic variance. In Schuecker et al. (2003), the analysis was extended to include cluster abundance using an empirical X-ray luminosity–mass scaling relation from Reiprich & Böhringer (2002), demonstrating that the combination of the two methods breaks the degeneracy between Ωm and σ8, in particular reducing the uncertainty on σ8 to the point where systematics related to mass estimation dominate (Table 2).
In principle, the spatial distribution of clusters can be employed in a simpler way, as has been done with individual galaxies, by using the baryon acoustic oscillation signature in the power spectrum as a probe of cosmic distance. Estrada, Sefusatti & Frieman (2009) and Hütsi (2010) respectively analyzed the correlation function and power spectrum of clusters in the optically selected maxBCG catalog, finding a weak (∼ 2σ) detection of the BAO peak. More recently, Balaguera-Antolínez et al. (2011) found no significant evidence for a BAO feature in the smaller, X-ray selected REFLEX II catalog.
Cluster gas mass fractions can be measured robustly using X-ray, or the combination of X-ray and SZ, data for dynamically relaxed clusters (Section 3). When measured from X-ray data, fgas values within a given angular aperture depend on cosmology as fgas(z) ∝ da(z)3/2, while the predicted fgas for a given cosmology is given by Equation 10. (A more detailed expression for the comparison of measured and predicted fgas values is given by Allen et al. (2008), who include terms accounting for instrument calibration, non-thermal pressure, and the relationship between the characteristic radius of the model, e.g. r2500, and the aperture of the measurement.) The apparent redshift dependence of fgas measurements on the cosmological background is illustrated in the bottom panels of Figure 9.
In principle, fgas measurements can be made at radii corresponding to any overdensity. In practice, this overdensity should be low enough (i.e. the radius large enough) that non-gravitational feedback effects do not introduce prohibitive scatter; but not so small (i.e. the radius not so large) that the measurements become dominated by the systematic limitations of the instruments. A variety of simulations indicate that radii ∼ r2500 are sufficiently large to benefit from low fgas scatter (e.g. Borgani & Kravtsov 2011), while at radii ≳ r500 uncertainties in the X-ray background and the impact of gas clumping can become a concern (Simionescu et al. 2011; see also Section 6.3).
Using this method, Allen et al. (2008) (see also Allen et al. 2004) obtained cosmological constraints using fgas measurements at r2500 from Chandra observations of 42 hot (kTX > 5 keV), relaxed clusters covering the redshift range 0.05 < z < 1.1. Their analysis incorporated weak priors on h and Ωb h2 from Hubble Key Project (Freedman et al. 2001) and big bang nucleosynthesis data, priors on the baryonic depletion and stellar mass fraction of clusters and their evolution (the term Υ(z) in Equation 10), and marginalized over systematic allowances accounting for instrument calibration and non-thermal pressure. From Equation 10, we see that the normalization of the fgas(z) curve, combined with the priors on h and Ωb h2, provides a constraint on Ωm; while the shape of fgas(z) allows dark energy parameters to be constrained via the apparent dependence of fgas on distance. The results for spatially flat, constant w models and non-flat ΛCDM models are respectively shown in Figures 11 and 15. For the non-flat models, the presence of dark energy is detected at high (> 99.99%) confidence, comparable to current SNIa results; the constraints, including systematic uncertainties, are Ωm = 0.27 ± 0.06 and ΩΛ = 0.86 ± 0.19, with the flat ΛCDM model yielding an acceptable goodness of fit. For constant w models, the fgas data are again competitive with other cosmological results, obtaining w = −1.14−0.35+0.27. The systematic, cluster-to-cluster scatter in fgas is small, < 7%, corresponding to only 5% in distance; this high precision results from the restriction to hot, dynamically relaxed systems for which total masses can be accurately estimated (Section 3.3.1).
Interestingly, for clusters with kT ≳ 5 keV, the measured fgas values show no dependence on temperature (right panel of Figure 15), indicating that, for the most massive clusters, the self-similar expectation of constant fgas with mass is realized. At lower temperature and mass (extending to the group scale), a trend of increasing fgas with temperature and mass is observed (e.g. Sun et al. 2009).
 |
Figure 15. Left: Joint 68.3% and 95.4% confidence regions on ΛCDM models with curvature from cluster fgas data at z < 1.1, compared with those from CMB data (Spergel et al. 2007) and SNIa (Davis et al. 2007). Inner, gold contours show results from the combination of these data. Right: fgas values as a function of ICM temperature. The measurements are consistent with a constant value over the temperature range explored (5 keV < kTX < 15 keV). From Allen et al. (2008). |
Ettori et al. (2009) have also applied X-ray data to the fgas test, using Chandra measurements at r500 for 52 clusters in the redshift range 0.3 < z < 1.3, adopting similar priors on h and Ωb h2 and marginalizing over a prior on Υ (assumed constant with redshift). However, their data set was not restricted to dynamically relaxed systems, resulting in significantly weaker constraints (Table 2).
LaRoque et al. (2006) employed Chandra X-ray and OVRO/BIMA SZ observations of 38 clusters in the redshift range 0.14 < z < 0.89 (with no restriction dynamically relaxed systems), finding fgas values consistent with previous X-ray work. (Their analysis did not take advantage of the relative normalization of the X-ray and SZ signals to simultaneously provide a second distance constraint; see Section 4.3.) They adopted the simpler approach of assuming constant fgas and marginalizing over its value, incorporating a WMAP prior on the total density, Ωm + ΩΛ. Although this explicitly ignores the information available from the normalization of fgas(z), their results clearly disfavor a dark matter dominated universe, preferring a low-density universe with dark energy (Table 2).
The different dependence on distance of the gas density inferred from X-ray and SZ observations of clusters can be exploited in a conceptually similar way to fgas data (Section 2.2.3). The most recent contribution is that of Bonamente et al. (2006), who measured distances to 38 clusters at redshifts 0.14 < z < 0.89. This cosmological test is intrinsically less sensitive to distance than the fgas test, with the signal proportional only to da(z)1/2 (Equation 11), and currently can constrain only one free parameter. Assuming spatial flatness and fixing Ωm = 0.3, Bonamente et al. (2006) obtained a constraint on the Hubble parameter, h = 0.77−0.09+0.11, consistent with results from other data such as the Hubble Key Project (Freedman et al. 2001) or the combination of fgas and CMB data (Allen et al. 2008). We note that other works using the same method have typically found somewhat lower best fitting values (h = 0.6–0.7; e.g. Grainge et al. 2002; Schmidt, Allen & Fabian, 2004), but these discrepancies are not significant given the systematic uncertainties.
4.4. High-Multipole CMB Power Spectrum
The CMB temperature power spectrum at multipoles ℓ ≳ 1000 encodes the thermal SZ signature of unresolved clusters at all masses and redshifts (Section 2.2.4). Although the primary CMB power decreases rapidly at these scales, extracting this cosmological information from the tSZ spectrum has proved challenging due to uncertainties in, e.g., the relevant observable–mass scaling relation at low masses and high redshifts; the population of infrared and radio point sources; the magnitude of the integrated kinetic SZ effect; and the form of the electron pressure profile at large cluster radii, where it is poorly constrained by current X-ray data (Sehgal et al. 2010; Section 6.3). The WMAP, SPT and ACT collaborations have all detected excess power at large multipoles, ℓ ≳ 3000. Subject to the systematic uncertainties mentioned, their results are broadly in agreement, and are consistent with estimates of σ8 obtained from studies of resolved clusters and the primary CMB (Dunkley et al. 2010; Lueker et al. 2010; Komatsu et al. 2011).
4.5. Evolving Dark Energy Models
As discussed above, current cluster growth and fgas data can constrain spatially flat models with constant w, finding consistency with the cosmological constant model (w = −1). Constraints on constant w models from the combination of these cluster data are shown in the left panel of Figure 16. To go beyond this simple description of dark energy, it is necessary to include cosmological data from additional sources in the analysis.
 |
Figure 16. Left: Joint 68.3% and 95.4% confidence regions for constant w models, using cluster growth (XLF; Mantz et al. 2010b) and fgas (Allen et al. 2008) data and their combination (green contours). These cluster data provide a 15% precision constraint on w (w = −1.06 ± 0.15) without incorporating CMB, SNIa or BAO data. Right: Constraints on parameters of the evolving w dark energy model in Equation 6 from the combination of cluster growth and WMAP (Dunkley et al. 2009) data (gray), and with the addition of cluster fgas, SNIa (Kowalski et al. 2008) and BAO (Percival et al. 2007) data (gold). The ΛCDM model (w(z) = −1) corresponds to the black cross. From Mantz et al. (2010b). |
Equation 6 provides a simple and commonly adopted model of evolving dark energy, in which the equation of state takes the value w0 at z = 0 and approaches w0+wa at high redshift. Constraints on this model were obtained from cluster growth data by Vikhlinin et al. (2009b) and Mantz et al. (2010b), assuming spatial flatness and in combination with external CMB, SNIa and BAO (and fgas, in the case of Mantz et al.) data. In both studies, the results are consistent with the ΛCDM model (w0 = −1 and wa = 0; right panel of Figure 16).
A slightly more general model due to Rapetti, Allen & Weller (2005),
 |
(25) |
also makes a smooth transition from one value at the present day (w0) to another at early times (wet), but has the advantage that the transition redshift, zt, can be marginalized over. (When zt = 1, Equation 25 reduces to Equation 6 with wa = wet − w0.) Mantz et al. (2010b) used the data sets above to obtain w0 = −0.88 ± 0.21 and wet = −1.05−0.36+0.20, again consistent with ΛCDM.
Absent a concrete physical model for dark energy, phenomenological models of evolving dark energy can take any form; for example, one possibility that has not yet been investigated using cluster data expands w(z) in principal components (e.g. Mortonson, Hu & Huterer 2010). Although these ad-hoc descriptions of dark energy are perfectly straightforward to apply to measurements of the expansion history, their applicability to an analysis based on the cluster mass function or power spectrum is less clear. Generically, descriptions of dark energy as a fluid with w ≠ −1 should include the effects of spatial variations in dark energy density (e.g. Hu 2005). However, the results from cluster growth so far have made use of mass functions from ΛCDM simulations, accounting for the value of w only in the expansion history (Vikhlinin et al. 2009b) or, at most, including the effect of density variations on the linear matter power spectrum (Mantz et al. 2008; Mantz et al. 2010b). In principle, the cluster mass function must also be adjusted to account for the behavior of fluid dark energy on smaller scales and in higher density environments. Encouragingly, preliminary work in this area suggests that the influence of dark energy on the mass function might be readily measurable, resulting in additional constraining power from clusters (e.g. Creminelli et al. 2010). Such improvements, however, might come at the cost of requiring additional sophistication in the theoretical description of dark energy (e.g. the dark energy sound speed and viscosity; Mota et al. 2007).