


2.2. Fluorescence
Sometimes we have the situation in which the atom or ion is in one of
its first m
lower-lying levels and then it is photoexcited to some higher-lying
level
 (e.g., by an
UV radiation field). Next it decays - either spontaneously or by
stimulated emission - back to
some different level among the first m levels. We call this
process fluorescence.
(e.g., by an
UV radiation field). Next it decays - either spontaneously or by
stimulated emission - back to
some different level among the first m levels. We call this
process fluorescence.
In this case it is easy to eliminate the level
 from the linear system of equations
(2), reducing its order by one.
from the linear system of equations
(2), reducing its order by one.
Initially, for notation purposes let us define:
The statistical equilibrium equation (2) for some level l
belonging to the first m lower-lying levels is:
where we have written only the terms involving the level
Solving for
n
with
And we have eliminated the equation involving
n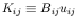
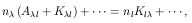
 . Whereas the equation for
level
. Whereas the equation for
level  will be:
will be:
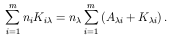
 in
eq. (11), substituting in eq. (10) and
introducing the indirect excitation rate from level i to
level j through level
in
eq. (11), substituting in eq. (10) and
introducing the indirect excitation rate from level i to
level j through level
 as:
as:
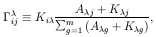
 ij
ij = 0; we can now rewrite
eq. (10) as,
= 0; we can now rewrite
eq. (10) as,
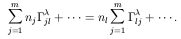
 .
Extending this reasoning to eliminate a whole set of µ
higher-lying levels is straightforward.
One simply replaces the indirect excitation rates in eq. (13) by the
corresponding
total indirect excitation rates:
.
Extending this reasoning to eliminate a whole set of µ
higher-lying levels is straightforward.
One simply replaces the indirect excitation rates in eq. (13) by the
corresponding
total indirect excitation rates: