


2.2.1. The Direct Method
Following Dinerstein (1990), the direct method can be broken down into 5 (easy) steps:
This step may seem trivial and self-explanatory. It assumes that you have taken proper care to reduce and calibrate your data. At the telescope, it is important to observe several standard stars (preferably from the HST spectrophotometric standards of Oke 1990). From my experience you can do a fairly good job just by following the standard procedures (with the addition of testing each step before moving on). I would recommend to the reader two guides available from NOAO (ftp: ftp.noao.edu; cd iraf/iraf/docs) "A User's Guide to CCD Reductions with IRAF" (Massey 1997) and "A User's Guide to Reducing Slit Spectra with IRAF" (Massey, Valdes, & Barnes 1992). Typically, one-dimensional spectra are extracted from long-slit (2-D) observations. Special care needs to be taken setting the extraction aperture width. The aperture should be sufficiently wide that small alignment errors do not give rise to systematic errors (this comes at a cost in signal/noise, but its worth the price). Additionally, one should avoid attempting "optimal" extraction. This works for stellar spectra that are inherently point sources and will be normalized, but not for extended nebulosities! And, finally, one should preferably integrate under the emission line profile (as opposed to fitting the line with a Gaussian profile). Fitting procedures can introduce systematic differences between high signal/noise and low signal/noise lines (and you will generally need to measure both accurately).
I'd like to insert yet another editorial comment here. I have had some experience trying to produce accurate emission line ratios from multi-order (echelle) spectrographs. Since the efficiencies change rapidly across the orders and since calibrating the relative efficiencies between orders is non-trivial, my experience tells me that emission line ratios from echelle spectrographs will never be as accurate as those derived from simple, long-slit spectrographs. I think that this is important, especially in the context of the design of spectrographs for the next generation of large telescopes - most of the planned spectrographs are echelle types (because of the ability to achieve high resolution and large wavelength coverage simultaneously). Thus, it is important to plan for long-slit spectrographs at (at least) a few of the large telescopes.
Because we know the theoretical emissivities of the recombination
lines of H, and because there are a number of H recombination lines
spread through the optical spectrum, it is possible to use the
observed line ratios to solve for the reddening of the spectrum.
The most recent H emissivity calculations are those provided by
Hummer & Storey (1987),
and, for the Balmer lines, these are very
similar to the values calculated by
Brocklehurst (1971).
If one assumes a reddening law
(f( ), e.g.,
Seaton 1979),
in principle, it is possible to solve for
the extinction as a function of wavelength by measuring a single
pair of H recombination lines. Values of
C(H
), e.g.,
Seaton 1979),
in principle, it is possible to solve for
the extinction as a function of wavelength by measuring a single
pair of H recombination lines. Values of
C(H ),
the logarithmic reddening correction at
H
),
the logarithmic reddening correction at
H , can be derived from:
, can be derived from:
where I(
In practice it is best to measure
several H recombination lines as this will provide both an estimate
of the effect of stellar absorption underlying the emission lines and
an estimate of the error in the measurement of the reddening.
Due to the lack of H recombination lines in the near ultraviolet, it
is possible to use He recombination lines in the same way. Here
one can use the emissivities calculated by
Smits (1991),
which, in general, agree well with those calculated by
Brocklehurst (1972),
but do differ significantly in some cases (and thus, the Smits
values are preferable).
There is a subtle problem with the reddening correction related to
the distribution of the dust. The above method assumes a uniform
"screen" of dust in front of the HII region. This is probably
reasonable for reddening by foreground Galactic dust, but will not
work so well if there is dust mixed within the HII region.
Israel & Kennicutt
(1980)
pointed out that the extinction derived
from Balmer line ratios tended to give lower values when compared to
values derived from comparisons between a Balmer emission line and
the thermal radio continuum emission. This implies clumpy
extinction, internal extinction, or both. This was supported by
detailed observations of Large Magellanic Cloud HII regions by
Caplan & Deharveng
(1986)
and Balmer line - Brackett line -
radio continuum emission comparisons of M101 HII regions by
Skillman & Israel
(1988).
Mathis (1983)
suggested that albedo
variations may also be partially responsible for the optical - radio
differences. While this effect is intrinsically interesting, it
appears to have only a minor effect on abundance determinations;
this is probably because the regions with the lowest amount of
reddening will dominate the integral spectrum, so the lower
values of reddening are probably appropriate. For a recent
discussion of this problem, see
Calzetti (1997).
Corrected emission line ratios should carry realistic errors.
With CCD detectors, which can be configured to be linear to within measurable
limits, it is possible to do a very accurate job of accounting for the
different sources of error.
Standard errors (
where C1 is the total number of counts (line plus
continuum and sky),
C2 is the continuum, S is the sky background in
a single row and
no and ns are the number of rows
summed over for the object and
the number of rows averaged for the sky, nAN2 accounts for
the readout noise, where n is the number of integrations,
A is the
area summed over in pixels, and N is the r.m.s. readout noise. The
fifth term represents the reddening error, where
By "local physical conditions" one means the temperature and
density of the gas. In fact, since the temperature is governed
by the balance between the heating and cooling processes, and since the
cooling is governed by different ionic species in different radial
zones, one expects different ions to have different mean
temperatures (cf.
Stasinska 1990;
Garnett 1992).
While this is best treated with a complete
photoionization model, a reasonable compromise is to treat the
spectrum as if it arose in two different temperature zones, roughly
corresponding to the O+ and O++ zones (since the
oxygen ions
play a dominant role in the cooling, this is a reasonable thing to do).
The average density can be derived by measuring the relative
intensities of two lines which arise from a split upper level. In the
"low density regime" collisional de-excitation is unimportant and
all excitations are followed by emission of a photon. The ratio of
the fluxes then simply reflects the ratio of the statistical weights
of the two levels. In the "high density regime'', where the level
populations are held at the ratio of their statistical weights,
the emission ratio becomes the ratio of the product of the statistical
weights and the radiation transition probabilities. In the intermediate
regime, near the "critical density" the line ratios are excellent
density diagnostics. The best known is that of [S II]
In order to convert these line ratios into densities, one needs to
know the energy level separations, the statistical weights of the
levels, and the radiative and collisional excitation and de-excitation
rates. Fortunately, one can use the five-level
atom program originally written by
De Robertis, Dufour,
& Hunt (1987)
which has been made generally available within IRAF by Shaw & Dufour
(1995; SD95).
This program has the additional great advantage that the
authors have promised to keep the input atomic data updated. I
recommend the SD95 article in PASP to any reader interested in
abundances from emission lines as it covers much more detail
than is allowed here. It is a well written and instructive article.
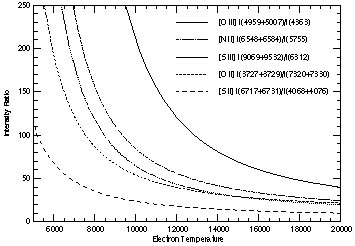
Figure 3. A diagram of the temperature
sensitive emission line ratios
for five ionic species observable in the optical/near-IR. These line
ratios were calculated with the five-level atom program of
Shaw & Dufour (1995)
at an assumed density of 100 cm-3.
Deriving temperatures in HII regions is pleasantly simple.
A glance at Figure 2 shows that the
ratio of the emission from an
upper level (an "auroral line", e.g.,
All of these ratios share the common problem that they are
increasingly difficult to measure at low temperatures (high
metallicities). For a sort of record in this game I direct the reader to
Kinkel & Rosa (1994).
They obtained a measurement of the [N II]
Ionic abundances can be derived by comparing the strength of an
ionic emission line to the strength of an H recombination line and then
comparing that ratio to the ratio of theoretical emissivities.
Stated as an equation:
where
The theoretical emissivities can be calculated from the program of SD95.
The emissivity for collisionally excited ions in the low-density limit is:
where Ni is the number density of the ion of interest,
Ne is the electron density, h is Planck's constant,
Normally, for observations of extragalactic HII regions, the observed
recombination
emission is restricted to H and He and the observed emission lines from the
heavier elements are all collisionally excited.
Because of this, absolute abundances (e.g.,
O++/H+) will have
a strong temperature dependence (and therefore the uncertainty can be
dominated by the uncertainty in the electron temperature).
Absolute abundances derived from recombination lines (e.g.,
He+/H+)
will have very small temperature dependences.
Similarly, relative abundances derived from two collisionally excited
lines (e.g., N+/O+) will have relatively small
temperature dependences.
Peimbert, Storey, &
Torres-Peimbert (1993)
have discussed the utility
of measuring absolute oxygen abundances using OII recombination lines;
unfortunately, given the relative weakness of these lines, this technique
will be limited to only the brightness Galactic nebulae.
When there are emission lines from all of the relevant ionic states,
the total elemental abundance is just the sum of the ionic abundances.
Unfortunately, this is rarely the case. This problem has given rise to
a number of empirical formulae for converting ionic abundances into
elemental abundances. Historically, some of these corrections were
based on the near coincidences of ionization potentials. For
example, consider oxygen:
In this case, O+ and O++ are both observable in
the optical
(
I close this discussion of the "direct method" by attempting to
answer one of the questions which came from the class, "Just how
accurately can one measure HII region abundances?" My answer:
if one has a sufficiently high quality spectrum, it is possible
to measure oxygen abundances in HII regions with accuracies of
roughly 10 - 20%! (even smaller uncertainties are routinely
encountered in the literature). This is certainly adequate for most
astrophysical applications. Such a tremendously valuable tool
can and should be used in a wide range of applications.
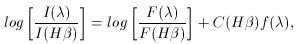
 ) is the
intrinsic line intensity and
F(
) is the
intrinsic line intensity and
F( ) is the observed
line flux corrected for atmospheric
extinction. Assuming a reddening law introduces a degree of
uncertainty. Studies in our Galaxy show that the reddening law shows
large variations between different lines of sight, but
these variations are most important in the ultraviolet
(Cardelli, Clayton,
& Mathis 1989).
Note also that the total measured extinction can have both
Galactic and extragalactic components.
) is the observed
line flux corrected for atmospheric
extinction. Assuming a reddening law introduces a degree of
uncertainty. Studies in our Galaxy show that the reddening law shows
large variations between different lines of sight, but
these variations are most important in the ultraviolet
(Cardelli, Clayton,
& Mathis 1989).
Note also that the total measured extinction can have both
Galactic and extragalactic components.
 L) for
the line strengths (L) can be calculated
from the following formula (where all numbers are in accumulated electrons):
L) for
the line strengths (L) can be calculated
from the following formula (where all numbers are in accumulated electrons):
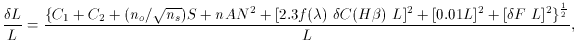
 C(H
C(H ) is the
error in C(H
) is the
error in C(H ), and
the sixth term accounts for errors in the
flat fielding (estimated at 1%). The seventh term represents errors in
the flux calibration, where
), and
the sixth term accounts for errors in the
flat fielding (estimated at 1%). The seventh term represents errors in
the flux calibration, where
 F is the r.m.s. relative
error for the fit
to the flux calibration points for the standard stars (typically 2%).
Leaving out the terms accounting for the errors in reddening or flux
calibration will result in unrealistically small errors.
F is the r.m.s. relative
error for the fit
to the flux calibration points for the standard stars (typically 2%).
Leaving out the terms accounting for the errors in reddening or flux
calibration will result in unrealistically small errors.
 6717 /
6717 /
 6731 which is sensitive in
the range from
102 to 104 cm-3 and can be observed at
moderate spectral
resolution. At higher spectral resolution, one can use several other line
pairs (e.g., [O II]
6731 which is sensitive in
the range from
102 to 104 cm-3 and can be observed at
moderate spectral
resolution. At higher spectral resolution, one can use several other line
pairs (e.g., [O II]  3726 /
3726 /
 3729).
3729).
 4363) relative to the
emission from a lower level (a "nebular line", e.g.,
4363) relative to the
emission from a lower level (a "nebular line", e.g.,

 4959,5007) will be highly temperature
sensitive. In Figure 3, I have used the program of SD95
to produce a comparison of five different temperature sensitive
emission line ratios. Note that I have used observer axes (linear)
as opposed to theoretician axes (logarithmic). This rather clumsy
representation emphasizes the ranges of utility for the different
line ratios (it can be difficult to accurately measure relative emission line
ratios with differences exceeding 200!). Clearly the [O III] ratio
is most useful at high temperatures,
although the
4959,5007) will be highly temperature
sensitive. In Figure 3, I have used the program of SD95
to produce a comparison of five different temperature sensitive
emission line ratios. Note that I have used observer axes (linear)
as opposed to theoretician axes (logarithmic). This rather clumsy
representation emphasizes the ranges of utility for the different
line ratios (it can be difficult to accurately measure relative emission line
ratios with differences exceeding 200!). Clearly the [O III] ratio
is most useful at high temperatures,
although the  4363 line will
always be relatively weak in
any HII region. On the other extreme, the [S II] ratio enjoys a wider
temperature range of applicability, but actually loses much of its
sensitivity to temperature above 15,000K (although there is still
a 30% change from 15,000K to 20,000K - maybe the choice of linear
axes isn't that great!). Of course, the ionization fraction will
affect the absolute line strengths, so [S II] temperatures are
rarely available for high temperature HII regions.
4363 line will
always be relatively weak in
any HII region. On the other extreme, the [S II] ratio enjoys a wider
temperature range of applicability, but actually loses much of its
sensitivity to temperature above 15,000K (although there is still
a 30% change from 15,000K to 20,000K - maybe the choice of linear
axes isn't that great!). Of course, the ionization fraction will
affect the absolute line strengths, so [S II] temperatures are
rarely available for high temperature HII regions.
 6584 /
6584 /
 5755 ratio of 200, implying a
temperature of
6820K and an almost solar oxygen abundance in the HII region Searle 5
in M101.
5755 ratio of 200, implying a
temperature of
6820K and an almost solar oxygen abundance in the HII region Searle 5
in M101.
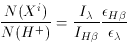
 is the emissivity of
the respective lines.
is the emissivity of
the respective lines.
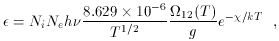
 the frequency of the transition,
the frequency of the transition,
 the average electron collision
strength from the lower level, g the
statistical weight of the lower level, k Boltzman's constant, T
the electron temperature, and
the average electron collision
strength from the lower level, g the
statistical weight of the lower level, k Boltzman's constant, T
the electron temperature, and  the
energy difference between the two electronic levels.
For recombination, the emissivities are significantly more complex, but,
in the end, their temperature and density dependences can be fitted with
suitable power laws.
the
energy difference between the two electronic levels.
For recombination, the emissivities are significantly more complex, but,
in the end, their temperature and density dependences can be fitted with
suitable power laws.
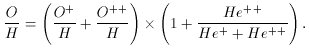
 3727 and
3727 and

 4959, 5007). The unobserved O3
state is corrected for by
assuming that the O3 zone is coincident with the
He++ zone
(based on the coincidence of the second ionization potential of He of
54.4 eV with the third ionization potential of O of 54.9 eV) which is
observable via the
4959, 5007). The unobserved O3
state is corrected for by
assuming that the O3 zone is coincident with the
He++ zone
(based on the coincidence of the second ionization potential of He of
54.4 eV with the third ionization potential of O of 54.9 eV) which is
observable via the  4686 line. This
is probably relatively safe (but this can be checked with far-IR
measurements of [O IV] emission at 26 µm). On the other
hand, similar ionization correction prescriptions have failed.
This is due, in part, to the fact that photoionization
cross-sections are complex functions and therefore ionization
potentials can only serve as approximate guides. Thus, modern
calculations of ionization correction factors rely on detailed
photoionization models (e.g.,
Mathis 1985;
Mathis & Rosa 1991).
For very detailed discussions I direct the reader to the cases of sulfur
(Garnett 1989),
nitrogen (Garnett 1990),
carbon
(Garnett et al. 1995a)
and silicon
(Garnett et al. 1995b).
4686 line. This
is probably relatively safe (but this can be checked with far-IR
measurements of [O IV] emission at 26 µm). On the other
hand, similar ionization correction prescriptions have failed.
This is due, in part, to the fact that photoionization
cross-sections are complex functions and therefore ionization
potentials can only serve as approximate guides. Thus, modern
calculations of ionization correction factors rely on detailed
photoionization models (e.g.,
Mathis 1985;
Mathis & Rosa 1991).
For very detailed discussions I direct the reader to the cases of sulfur
(Garnett 1989),
nitrogen (Garnett 1990),
carbon
(Garnett et al. 1995a)
and silicon
(Garnett et al. 1995b).