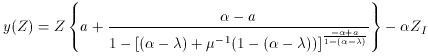3.2. Absolute Abundances: Some Simple Formulae
The formulae for chemical evolution have developed over the years. If I wanted a student to fully appreciate the development of these formulae, I would direct them to read Schmidt (1963), Searle & Sargent (1972), Larson (1972), Audouze & Tinsley (1976), Pagel & Edmunds (1981), Peimbert & Serrano (1982), Chiosi & Matteucci (1982), Matteucci & Chiosi (1983), and Edmunds (1990). If they ever returned to my office, I would further direct them to concentrate on our galaxy and read Pagel & Patchett (1975), Tosi (1988), Pagel (1989), and Matteucci & Francois (1989).
However, I do not expect the reader of this chapter to perform this exercise. Instead, I would direct them to the concise summary given in Peimbert, Sarmiento, & Colin (1994) (also found in Peimbert, Colin, & Sarmiento 1994). I will run through their equations, adding my own personal notes. I am suggesting that this set of equations should be considered as the ``standard set". That is, I regard this set of equations as a good background from which to consider many of the possible routes of chemical evolution.
Starting with the definition of the yield (often referred to as the net, real, or true yield):
where the numerator is the mass of heavy elements returned to
the ISM (not just created) and the denominator is
the entire mass converted into stars which is not returned to the
ISM (low mass stars, remnants, planets); integrated over the entire IMF.
An element specific yield can be written as (for example, here
we use oxygen):
For a specific volume (e.g., defining a volume surrounding a galaxy or
a zone of a galaxy), the mass in baryons will change if
there is inflow or outflow.
The total mass in gas is reduced by the star formation rate
(
where R is the mass fraction returned to the ISM. Note the
difference between R, which is all of the mass which has been
incorporated into stars and then returned to the ISM and y which is
the mass of an element that is produced in the stars and then
returned to the ISM.
Thus, the change in the mass of heavy elements can then be represented as:
where the subscript on ZI indicates that it is the
metallicity of the inflowing gas (in some cases assumed to be zero).
Meanwhile, the heavy element mass fraction Z will change as:
Then from the equation above and introducing µ =
Mg / Mb:
Dividing the last two equations yields the following relationship:
Peimbert et al. emphasize that the above equations hold for the
``instantaneous recycling approximation" (IRA). The IRA is deemed
suitable for elements that are created primarily in high mass stars
so that the newly created elements are returned to the ISM in a
period of time which is short compared to the lifetime of an ``average"
star. Presently, there is some debate concerning the applicability of
the IRA even for elements (like oxygen) which fit this bill. The
problem is the uncertainty of detecting these elements. If one wants to
apply an observational check of the chemical evolution under this prescription,
it is important not only that the elements are returned to the ISM in
a short time, but also that they show up in an observable phase within
that short time.
A very special case of the above equation results in the absence of flows.
The equation then reduces to the case of the ``simple closed box'' model
(Schmidt 1963;
Searle & Sargent 1972):
If galaxies were well described as simple closed boxes, then the
diagnostic power of this equation would be tremendous. Measuring the
gas mass fraction and the ISM abundance would measure the yields of
each of the observable elements! There are, unfortunately, a number
of pitfalls. The first, and obvious one, is that galaxies may not
behave as simple closed boxes. There is evidence that infall is
important for large galaxies
(Pagel & Patchett 1975)
and it is very popular to consider outflow as likely for dwarf galaxies
(e.g.,
Dekel & Silk 1986;
Marlowe et al. 1995).
Even if galaxies behaved as simple closed
boxes to first order, there are other complications. Measuring the
appropriate gas mass fraction is problematic. This is the ratio of the
baryonic mass in gas to the total baryonic mass (stars + gas).
The ubiquitous presence
of dark matter makes it difficult to identify the precise mass in stars.
There is also the question of the appropriate measurement of gas mass.
Not only is there uncertainty regarding the molecular gas masses in
galaxies (cf.
Israel 1988a,
b;
Maloney & Black 1988),
but galaxies show a large range in gas distribution size relative to stellar
distribution size. Should the gas at large radii (which may not be
available for star formation and may not be participating in the
enrichment) be included in the calculation of gas mass? Finally,
we must consider the possibility that newly synthesized elements are
retained in a hot phase and not well mixed into the more easily
observable cool phases. The above is not meant as a discouragement,
only a warning.
Note that an optimistic observer can still salvage something from this.
By measuring Z and µ and calculating y from
the above formula,
it is possible to obtain an ``effective yield." While this may not
be directly related to the yield that one would calculate from a
detailed understanding of stellar nucleosynthesis, stellar evolution, and
the IMF, nonetheless, effective yields may prove to be a very useful
tool in comparing galaxies and their chemical evolutionary states.
Undaunted, we then follow Peimbert et al. as they consider the complication of
adding inflow. When this is set equal to the star formation rate, one gets:
Setting the star formation rate equal to the inflow rate is not
only a neat trick that results in a relatively simple formula, but it may
have a good physical motivation. If galaxies obey some sort of star
formation law which requires a threshold gas density (e.g.,
Kennicutt 1989)
then it makes good sense to equate the inflow rate with the
star formation rate.
Dropping the assumption that the inflow equals the star formation rate
results in a significantly more complex relationship. If the inflow rate is
parameterized as fI =
(Things are getting considerably complex at this point).
If, on the other hand, the system is losing gas (parameterized as
fO =
And, finally, combining inflow, outflow and allowing for a linear metallicity
dependent yield (a), one has:
OK, at this point, I believe that the equation has become so complex
that it is not possible to tell by inspection how the yield and the gas mass
fraction are related over the large range of possible parameters. Is this
equation unnecessarily complex? I don't think so. Inflow and outflow are
well motivated ideas, and metallicity dependent yields are also
(Maeder 1992;
see next section).
Fortunately, this equation is still simple enough that it can be coded
relatively easily and played with by running various numerical models.
This is where I will leave off, encouraging the motivated reader to do so.
At this point, I will reiterate and reinforce my earlier point - the key
to observational progress in this field lies in cleverly isolating
variables (i.e., using the vast diversity of galaxies or focussing on
elements of different origins as described in the next section).
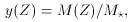
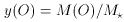
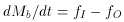
 )
and increased by the return from the various phases of stellar
evolution:
)
and increased by the return from the various phases of stellar
evolution:
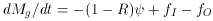
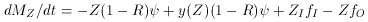
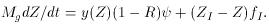
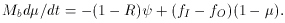
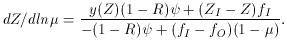
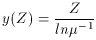

 (1 - R)
(1 - R)
 , then the result is:
, then the result is:
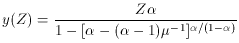
 (1 -
R)
(1 -
R)  ), then one has:
), then one has: