4.3. Relative Abundance Patterns
4.3.1. C/O
The relative abundances of carbon and oxygen are important for a variety
of problems, including: (1) C and O
are important sources of opacity in stars. Knowledge of the
time evolution of C and O abundances is necessary to properly model the
structure and evolution of stars at different ages and abundances,
(2) The formation of the CO molecule in the ISM should be regulated by the
relative abundances of C and O at some level, so an understanding of the
variation of C/H and C/O in the ISM is relevant for modeling the formation of
CO molecules and the possible effects of abundance variations on the
I(CO)/N(H2) relation,
(3) There is evidence that the interstellar dust-to-gas ratio is related to
the interstellar carbon abundance (Mathis 1990),
so knowledge of C
abundances in a variety of environments is relevant to understanding the
amount, composition, and evolution of dust in those environments,
(4) In theory, oxygen is synthesized almost entirely in massive stars
(M > 10 M
), while
carbon is produced in both massive and intermediate
mass stars. Thus, the ejection of some carbon is delayed in time with respect
to oxygen, so the C/O ratio offers a potential "clock" for determining the
relative ages of stellar systems.
|
|
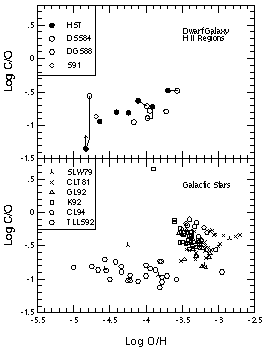
Figure 8. (upper) The C/O abundance ratio in irregular galaxies vs. O/H. Filled circles are from FOS spectra; unfilled squares are from IUE observations for Orion (average from the literature) and NGC 2363 (Peimbert et al. 1986). The stars represent the mean abundances in Galactic B stars determined by Gies & Lambert (1992) and Cunha & Lambert (1993). The solar system value is also shown (Grevesse & Noels 1993). (lower) C/N abundance ratio vs. O/H in irregular galaxies. Symbols are the same as above. (From Garnett et al. 1995a) |
Garnett et al. (1995a)
have used the HST to observe HII regions spanning a range in abundance.
The resulting carbon and oxygen abundances for the targets from our sample are
displayed in Figure 8 (upper), plotted as log
(C/O) vs. log (O/H).
The data show an apparently continuous increase in C/O with increasing O/H in
these metal-poor systems. By comparison,
a simple chemical evolution model with instantaneous recycling predicts
constant C/O if both C and O are primary elements, or C/O
O/H if O is
primary and C secondary. Since only primary sources of C are known to exist,
the trend in Figure 8 suggests that either the
instantaneous recycling
approximation does not hold for both C and O or that the yield of C varies with
respect to O (or both). This is discussed in detail below.
Figure 8 (lower) also shows the variation of C/N with O/H, with nitrogen abundances obtained from the sources of optical spectra listed above. If we exclude the Galactic points (Orion, B stars, and solar system), then a trend of increasing C/N with O/H is apparent. A larger sample of galaxies is needed to confirm and delineate the trend more clearly, but it appears that the pattern of chemical evolution seen in the dwarf galaxies does not fit in with that seen in our own galaxy.
|
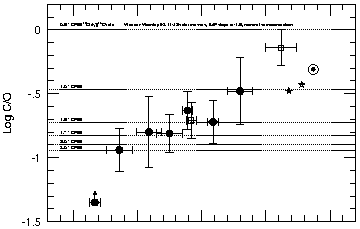
Figure 9. The C/O abundance ratio versus O/H for H II regions in irregular galaxies and Galactic stars. (Upper) New HST HII region abundances are compared with previous results from IUE observations. The open circles come from Dufour, Schiffer, & Shields (1984), the open hexagon represents IZw18 as from Dufour, Garnett, & Shields (1988) as adjusted by Dufour & Hester (1990), and the open diamond represents UGC 4483 as reported by Skillman (1991). (Lower) Galactic stars are presented. The data are taken from Sneden, Lambert, & Whitaker (1979), Clegg, Lambert, & Tomkin (1981), Gies & Lambert (1992), Kilian (1992), Tomkin et al. (1992), and Cunha & Lambert (1994). (From Garnett et al. 1995a). |
Figure 9 presents a comparison of our new results with previous results found in the literature. Here we are interested in two questions, (1) do these new results agree with previous results on C/O measurements of H II regions in dwarf galaxies and (2) is the pattern of C/O versus O/H seen in the dwarf galaxies similar to that seen in our Galaxy?
The top panel of Figure 9 addresses the first question. Here the points from Figure 8 are plotted along with results from IUE observations taken from the literature. Points which represent observations of the same galaxy are connected, showing a good agreement between the new and old observations.
The bottom panel of Figure 9 presents C/O and O/H measurements of Galactic stars taken from the literature. There is considerable scatter in log (C/O) for the disk stars, with an average value of about -0.4. For the halo stars, log (C/O) is fairly constant at -0.9 (with a scatter consistent with observational errors). If the trend of increasing C/O with O/H seen in the H II regions of dwarf galaxies is supported by more observations, then a clear difference is emerging between the abundance pattern seen in our Galaxy and the dwarf galaxies.
Figure 9 prompts one more philosophical aside. Plots of relative abundance versus metallicity in our Galaxy (lower panel) hopefully allow us to trace the relative abundances in a single system with time. Is this true for the upper panel? Obviously not. These are different systems, and they are all sampling the abundances at the present epoch. From the metallicity-luminosity relationship, we know that the abcissa of the upper panel of Figure 9 is really a ranking in the sizes (masses) of the systems (in addition to the chemical maturity), so it is unlikely that the low metallicity systems will evolve into the high metallicity system (i.e., that they will evolve from low mass to high mass). On the other hand, if different galaxies evolved with vastly different star formation histories and/or vastly different IMFs, we would not expect to see the smooth relationships we often find when comparing different systems in this way. This is probably telling us that galaxies all evolve obeying some simple (universal?) physical principles.
|
|
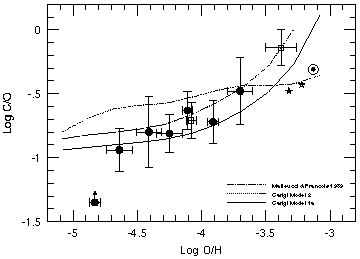
Figure 10. (upper) Comparison of our C/O
abundance ratios in irregular galaxies with
the results of stellar nucleosynthesis calculations
(Weaver & Woosley
1993).
The horizontal dotted lines indicate the value of the C/O ratio one obtains
by integrating the C and O produced by massive stars over a mass range 11 - 42
M |
Before proceeding with an interpretation of these trends, I would like to make
a small aside to return to one of the themes I discussed in my introduction -
the possibility of using ISM abundances to give insight to better understand
stellar physics.
16O is predominantly a product of
-particle captures
onto 12C
during the He burning phase of stellar evolution. The amount of O ejected by a
star depends on its mass.
Stellar evolution models generally show that 10
M
is the smallest star that can produce and eject new
oxygen. 12C is also
produced during He burning through the well-known
"triple-" reaction.
Theoretical models indicate that carbon can be ejected not only by
massive stars, but also by intermediate mass stars
(
2-8
M) through the
convective dredge-up of freshly-synthesized carbon during the asymptotic
giant branch evolution phase of these stars. Measurements of carbon abundances
in planetary nebulae show that some of them have enrichments of carbon,
confirming
that dredge-up does occur in at least some intermediate mass stars.
The relative amounts of C and O produced during He burning are sensitive to
the 12C(,
) 16O
nuclear reaction rate, as demonstrated by the models of
Weaver & Woosley (1993;
hereafter WW93). The
value of the cross section for this reaction has been a source of considerable
uncertainty (cf.
Rolfs & Rodney 1988).
Some attempts have been made to determine the rate empirically. Arnett (1971),
for instance, tried to constrain the reaction rate by comparing the solar
system C/O ratio with the predictions of stellar nucleosynthesis. This
analysis assumed that both C and O are produced in massive stars only and that
the C/O ratio does not evolve with time. Clearly, however, the observations of
C/O in Galactic stars and extragalactic H II regions show that the C/O ratio
has evolved. WW93 tried a similar approach to the problem,
comparing their results for massive star nucleosynthesis with the solar system
abundance pattern, but excluding carbon in the comparison. They
found that a reaction rate of 1.7 ± 0.5 times the Caughlan & Fowler
(1988, CF88)
rate produced the best match to the solar system abundance distribution for
elements between O and Fe. New laboratory measurements of the
12C(,
)16O cross
section have been reported by
Buchmann et
al. (1993) and
Zhao et al. (1993).
In terms of the commonly used
astrophysical S factor, S(E), Buchmann et al. measured a value
SE1(0.3 MeV)
= 57 ± 13 keV-b, while Zhao et al. obtained a value
SE1(0.3 MeV) =
95 ± 32 keV-b for the same reaction. For comparison, WW93's best
estimate corresponds to SE1(0.3 MeV) = 102 ± 30 keV-b.
With these new observations, it is possible to
estimate the 12C(,
)16O
reaction rate by comparing the stellar nucleosynthesis results of WW93 with
the C/O ratios measured in the most metal-poor galaxies. If we assume
that (1) the most metal-poor galaxies in our sample have abundance
ratios dominated by nucleosynthesis from massive stars and (2)
the stellar IMF does not change
significantly with metallicity, then the asymtote of the C/O
abundance ratio can provide a measure of the reaction rate.
Figure 10 shows our
observed C/O ratios overlaid with the C/O ratios obtained by
integrating the WW93 results over the stellar mass range 11-42
M
with an IMF slope of -1.5 (taken from their Table 7). The
horizontal dotted lines show the theoretical integrated C/O ratios obtained
for different values of the
12C(,
)16O
rate in units of the CF88 rate.
The observed C/O ratios in our three most metal-poor
galaxies (not including IZw18) are consistent with WW93's estimate for
12C(,
)16O.
While this comparison should be viewed with caution because of a number of
additional uncertainties which can affect the results (e.g., the effects of
stellar mass loss and mixing on stellar evolution and nucleosynthesis
have only recently been explored extensively, e.g.,
Maeder 1992;
Woosley, Langer &
Weaver 1993),
it is instructive to see what types of observations
can be planned to cross the bridge between ISM and stellar physics.
Returning to the interpretation of the observed abundance ratios, it is clear that the C/O abundance ratio in low-metallicity systems is lower than in the solar neighborhood. The low C/O ratios we observe in our most metal-poor galaxies are consistent with the C/O ratios observed by Reimers et al. (1992) in Lyman-limit and metal-line absorption systems toward the QSO HS1700+6416. These results combined with ours clearly show that the C/O ratio has evolved from low values at early times to the present-day "cosmic" ratio.
Lets consider the trend in Figure 8 within the framework of the simple closed box model of chemical evolution and the instantaneous recycling approximation. Since both C and O should be primary elements, the simple model predicts that C and O should maintain a constant ratio. This prediction is clearly at odds with the observations.
There are several possible ways to explain the variation in C/O with O/H:
(1) Breakdown of the instantaneous recycling approximation.
While the IRA may apply to oxygen, it is less likely to apply to carbon. The low C/O ratios in the dwarfs may indicate that their stellar populations are, on average, much younger than more massive galaxies. This is another way of saying that the star formation histories of the galaxies may be different.
(2) Variable IMF.
A comparison of the upper and lower panels of Figure 8 proves interesting. Note the abrupt drop in C/N between the solar neighborhood objects and the more metal-rich dwarf galaxies (NGC 2363 and LMC), which is attributable to much larger nitrogen abundances in the Galactic nebulae. In contrast, the C/O ratio maintains a smooth upward trend including the Galactic objects. Taken together, these features suggest that either the nucleosynthesis of C is largely decoupled from that of N or that the chemical evolution histories of the dwarfs and the Galaxy are very different. For this to be accounted for by changes in the IMF, one possibility is that C and O production is dominated by massive stars, while N comes mainly from intermediate mass stars (IMS). Another possibility is that N and C are both produced mainly in intermediate mass stars, but in different mass ranges. (But remember that there is a lack of evidence for variable IMFs.)
(3) Variable yields.
Carigi (1994) has calculated chemical evolution models for the Galaxy which take the Maeder yields for massive stars into account. Her models show a significantly steeper increase in C/O with O/H than the older models of Matteucci & François (1989), which used massive star yields from Woosley (1986). The results for Carigi's models 1a and 2 are plotted with our data in the lower plot of Figure 10. The models reproduce the trend in the data fairly well. Prantzos, Vangioni-Flam, & Chauveau (1994) have computed similar models for the solar neighborhood also, and find similar results.
While the present data do not allow for a definitive choice between the above alternatives, I think that choice (3) is the most probable at this time. Future observations of objects which show a range in C/O at a constant O/H may help in constraining the choices.