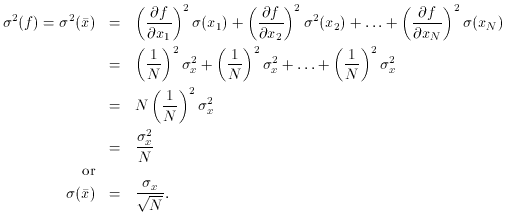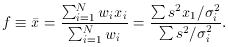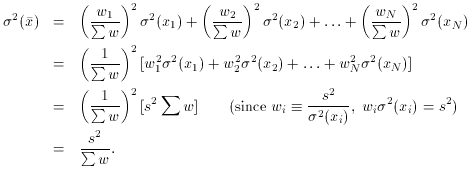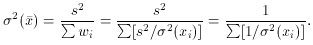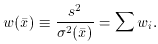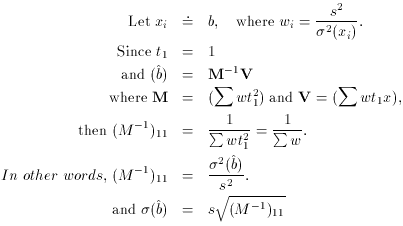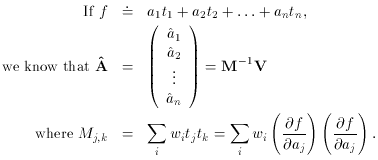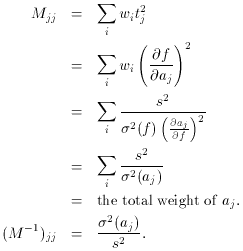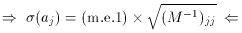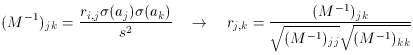A. Parameter error estimates
In my previous lecture, I promised that I would explain how to derive standard-error estimates for the derived fitting parameters. To provide some background for the subject, let's take a look at how errors propagate. Let's say you have some continuous function f of a variable x, and that any specific value of that x is subject to random errors. To first order the standard error of the f corresponding to that x is given by
If f is a linear function of x then this equation
is exact; if the
function is non-linear then this relationship is only good, as I said,
to first order. Now if f is a function of many independent
variables
x, then to obtain the overall standard error of f you have
to add the squares of the individual contributions, like this:
Just for practice, let's apply this equation to a very simple linear
function. Let f be the mean of N independent
determinations of some
quantity x, where each x measurement is subject to a
constant standard
error,
Thus, we finally arrive at something you knew all along, namely when
you take the average of N independent measurements of some quantity,
the standard error of the mean decreases as the square root of N.
Now let's look at the case where the standard errors of the individual
x measurements are not the same, so we want to take a
weighted mean of
the x measurements. The weights are given, as usual, by the inverse
squares of the standard errors:
When we now propagate the errors through this equation, we see
So we conclude that
Conversely, we can also say
In other words, the weight of the weighted mean is equal to the total
weight of the individual observations - an easy fact to remember.
So why did I bother to go through all that? Well, let's look at the
problem again, but this time using the least-squares formalism
presented in the last lecture:
I'm not going to give you a formal proof - they can be found in more
advanced texts on maximum-likelihood techniques - but the same sort of
conclusion can be drawn with greater generality:
The diagonal elements of M are
So...
As a footnote: the off-diagonal elements of M-1
give the correlation
coefficients, rk, k between the parameters:
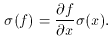
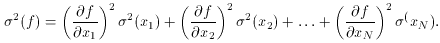
 x. Then
f
x. Then
f 
 = (x1 +
x2 + . . . xN) / N, and the
square of the random error of f is given by
= (x1 +
x2 + . . . xN) / N, and the
square of the random error of f is given by