Next Contents Previous

PROFILE FITTING - ALLSTAR

Now that we have that dreadful discussion out of the way, we come to the heart of crowded-field photometry - the actual fitting of the model stellar profile to star images. I've already explained the basic principle several times. You simply use non-linear least squares to fit the model profile to the actual data, to determine four unknowns per star: the x0, y0 position of the star's centroid, the star's brightness, and the local sky brightness (6). If two stars are blended together, then you solve simultaneously for seven unknowns: two x0's, two y0's, two C's, and one B. If three stars are blended, you solve for ten unknowns, and so on.

To work this method up into a practical computer program, however, there are some details to consider. The first of these is you must decide exactly which pixels to use in the fits for any given star. In the examples of two-dimensional profile fits that I showed you two days ago, I fit the model profile to all pixels contained within a large rectangular area around the star. This is not really a very practical definition of the "fitting region" in a crowded field. Say you have a frame where the stellar images have a full-width at half-maximum of 3 pixels. A bright star in such a frame might have a profile which could be traced out to a radial distance of 12 pixels. If you were to use a rectangular box including the entire stellar profile, it would have sides of ± 12 = 25 (think about it) pixels and would contain 625 pixels. This is a lot of data for one little star. Worse, a rather crowded frame, in my experience, could contain as much as one star per every 30 - 50 pixels (a 300 x 500 frame with critical sampling, if it is crowded, can contain 3,000 - 5,000 stars that are worth trying to reduce). The "fitting region" around the star of interest, then, may be expected to contain ~ 20 other stars: if you try to reduce simultaneously all stars that are blended - in the sense that their fitting regions contain some pixels in common - you'll surely be reducing every star in the frame all at once, and you'll be trying to invert 15,000 x 15,000 matrices. Forget it.

Instead, you must adopt much smaller fitting regions around each star. In the sorts of frames I was talking about earlier, with FWHM ~ 3 pixels (HWHM ~ 1.5 pixels), I've been using circular fitting regions with radii of order 2.5 - 3 pixels. (Why do some programs use a rectangular fitting region? Sure, it's a bit easier to program, but stars are round, and why should a pixel which is 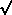sqrt2 . 3 pixels from the star's centroid in a diagonal direction be included in its solution, while one which is the same distance away to the right or left or above or below is excluded?) In the simultaneous reductions of every star in a CCD frame, ALLSTAR starts with the initial guesses for all the unknown parameter values (x0, y0, and C for every star in the frame), subtracts the model profiles implied by these values from the image and, using the residuals from these subtractions, does a single nonlinear-least-squares iteration for every star in the frame. For each individual star, ALLSTAR considers only the residuals in the 2.5 - 3-pixel circular fitting region if the star is isolated. However, any stars whose fitting regions overlap are included in the same matrix inversion for this iteration. Then, after a single correction has been derived for each of the parameters of every stars in the frame, the entire profiles implied by the new values of x0, y0, and C - out to the full radius to which the PSF has been defined - are subtracted from the frame, and another iteration is performed on every star in the image based upon the new set of residuals. When any individual star seems to have fully converged to its "best" parameter values, these values are written to a disk file, the star is subtracted permanently from the image, and subsequent iterations continue with whatever stars are left. As more and more stars converge and are removed from the problem, the iterations progress faster and faster. It gets quite exciting toward the end.

A tiny fitting region for each star is possible because, while the profile for a bright star can extend many HWHM's from the center, really most of the photometric and positional information is contained within a couple of HWHM's. A tiny fitting region is necessary, because otherwise the solutions become completely intractable if there are more than a couple hundred stars in the frame. However, such tiny fitting regions have their own problems. In particular, because the stellar profile has not, in general, gone to zero surface brightness by the time the edge of the fitting region has been reached, it is possible to get into paradoxical solutions. For instance, when some particular pixel is included in the fitting region for the star, the star's centroid may get corrected so as to shift that pixel out of the fitting region; then, without that pixel, the solution corrects the star's centroid so as to bring that pixel back into the fitting region. The solution could wobble back and forth forever. Alternatively, you might have a situation where including a particular pixel in the solution keeps the pixel in the fitting region, and excluding it keeps it out of the fitting region: two slightly different starting guesses could then come up with completely different final answers for the same star from the same data. For each of these two situations, there is no good way to determine which of the two possibilities is the "better" answer without including every pixel in the frame in the solution for every star in the frame. One practical answer is to increase the adopted radius of the fitting region slightly, and then to taper off the weights assigned to the pixels as the edge of the fitting region is approached, using some arbitrary radial weighting function like that illustrated in Fig 4-4. Then whatever pixel was causing the solution either to dither or to split into two distinct answers can achieve partial weight somewhere out near the edge of the fitting region, and the solution can happily converge to some balanced intermediate value. I confess that I can't demonstrate analytically that this intermediate solution is "better" than either of the two previous alternatives, but intuitively I suspect that it is. After all, partial weights for pixels straddling the edge of the fitting region is physically sensible: partial weights for pixels partially in the fitting region. The precise formula which one uses to compute those partial weights won't be very important. I can say on the basis of considerable experience that at least this method allows the solution to converge to some reasonable value, so you can finish reducing this frame and get on to the next one.

Figure 4_4
Figure 4-4.

You may have noticed that a couple of paragraphs back, I said nothing about ALLSTAR correcting the sky value associated with each star. Of course it could do this - one would merely solve for 3N + 1 unknowns (for a constant sky level, 3N +3 for a sloping plane, ...) - but in general I don't. Because only a few pixels per star are included in fits, and those pixels are restricted to radii which are pretty much still well within some star's profile, it is not really practical - under the conditions I have described - to redetermine the sky as part of the least-squares fits. Instead, I usually assume that the sky value determined during the aperture photometry is correct, and use that. I think that this is not necessarily a Bad Thing. In the other method, where the stellar profile plus the sky value are all determined together by a least-squares fits to some large region, there may be at most some hundreds of pixels which can contribute meaningfully to the determination of the sky value. In contrast, for the sky annulus which is used to determine the sky value in the aperture photometry, I typically set an inner radius ltapprox 20 pixels and an outer radius ~ 35 pixels. This region thus contains some pi . (352 - 202) = 2600 pixels, as compared to only a few hundred; on our VAX 11/780 or a microVAX, the Kitt Peak algorithm can get a sky value from these 2600 pixels in considerably less than a second, while a full-blown nonlinear least-squares solution to 625 pixels would take far longer than this. Furthermore, the algorithm which the Kitt Peak software uses is highly robust against contamination by other stars or by defective pixels, while a standard least-squares solution in the big rectangular area would have to be very careful to avoid being affected by such problems. A little circular fitting region of radius, say, 3 pixels would contain some 28 pixels in all, but because of the tapered radial weights, the effective area would be somewhat smaller - maybe 20 pixels. The probability of contamination in this area is ~ 625/20 = 30 times smaller than in the big area.

Figure 4-5
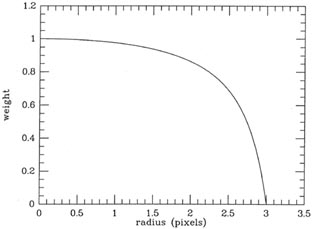
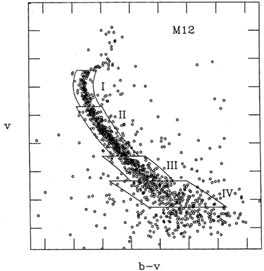
Figure 4-5.

All of the handwaving arguments in the world won't convince you that it's OK not to determine the sky level as part of the least-squares profile fits (they didn't convince me, anyway), so I ran some tests. Figs. 4-5 and 4-6 show two instrumental color-magnitude diagrams; Fig. 4-5 is for the globular cluster M12, and Fig. 4-6 is for our old friend 47 Tucanae, with a little bit of the Small Magellanic Cloud in the background. Each of these color-magnitude diagrams is based on a single pair of frames. I repeated the reductions of these four images, using NSTAR (an earlier, slower, more primitive version of ALLSTAR), and seven sets of conditions: (1) adopting the sky-brightness value which PHOTOMETRY obtained for each star as correct, and using a radius for the fitting region of 2 pixels; (2) - (4) determining a constant sky-brightness value for each group of blended stars, with fitting radii of 2, 4, and 6 pixels; and (5) - (7) fitting a sloping plane to the sky underneath each group of blended stars, with fitting radii of 2, 4, and 6 pixels. Tables 4-1 and 4-2 show the results of these tests, in the form of the mean absolute half-width of the cluster sequence contained in each of the boxes in Figs. 4-5 and 4-6 (note that box IV in the 47 Tuc diagram is the upper main sequence of the SMC; the gap between boxes I and II in this figure is to exclude the red horizontal branch of the SMC, which lies on top of 47 Tuc's main sequence at this point). For the 47 Tuc reductions, I have also listed the execution time required to reduce the two images. As you can see, solving for the sky as part of the profile fits increases the scatter, typically by of order 18%, while increasing the typical execution time from 12.4 hours to 18.3 hours: in effect you are getting 28% less information while doing 46% more work.

Figure 4-6
Figure 4-6.

Of course, simply adopting the PHOTOMETRY values of the sky brightness is not the best idea if the sky changes significantly on the scale of the sky annulus. In 1988, Bill Harris and I did a pretty extensive study of the globular cluster M92. There, both the cluster background and some scattered light from bright stars just off the side of the frame made for a spatially varying sky brightness. What we did was to perform one set of profile fits, employing the sky values from PHOTOMETRY. We then subtracted all the visible stars from the frame, and passed a median filter over the image: for each pixel in the subtracted image, we determined the median of all pixel values in a circular region centered on that pixel. Where a pixel was "missing," whether because it was "bad" or because the circular region extended beyond the edge of the frame, the diametrically opposite pixel was also omitted from the median. This properly preserves the brightness gradients of the original image in the smoothed one, but the smoothed image does get noisier toward the edges and in the corners. We used a radius of 12 or 13 pixels for the circular region - large compared to a star, but small compared to PHOTOMETRY's sky annulus. This smoothed sky background was subtracted from the original image, and then a constant value was added back in (this was necessary to make ALLSTAR's error analysis come out close to right). Thus, our image now had a fiat, known sky brightness; the profile fits were repeated using this constant sky brightness for the reduction of each star. Our conclusion from extensive artificial-star tests was that, at the completeness limit of our data (defined for the moment as that magnitude where a star had a 50% probability of being discovered in any particular image), we tended to overestimate the brightnesses of our stars systematically by maybe 0.02 mag approx 2%. If this is attributed to a systematic error in the sky-smoothing algorithm, then taking into account the relative surface brightness of the sky and a star at the detection limit, this would imply that we were systematically underestimating the sky brightness by maybe 0.1%. This in a pretty crowded field: of order 3,000 - 3,500 detectable stars in a 300 x 500 image, or < 50 pixels per star. However, there are other pretty good reasons why we may have been measuring our stars systematically too bright, so the systematic underestimate of the sky brightness may have been less than this.

Table 4-1. Observational Scatter on the Main Sequence of M12
Sky-fitting <Delta> <|Delta|> sigmahatb-v n <Delta> <|Delta|> sigmahatb-v n
method (mag) (mag) (mag) (mag) (mag) (mag)
13.41 < v < 14.70 14.70 < v < 16.46
|Delta| < 0.07 |Delta| < 0.09
none, r=2 -0.0032 0.0151 0.0189 121 +0.0008 0.0228 0.0288 343
flat, r=2 -0.0074 0.0186 0.0236 122 -0.0006 0.0277 0.0364 339
flat, r=4 +0.0024 0.0208 0.0270 116 -0.0033 0.0282 0.0374 330
flat, r=6 +0.0072 0.0228 0.0310 114 +0.0018 0.0298 0.0411 324
plane, r=2 -0.0056 0.0196 0.0251 118 +0.0012 0.0283 0.0376 341
plane, r=4 +0.0034 0.0200 0.0257 115 -0.0057 0.0270 0.0351 333
plane, r=6 +0.0036 0.0234 0.0326 94 +0.0040 0.0283 0.0376 259
16.46 < v < 17.34 17.34 < v < 18.27
|Delta| <0.15 |Delta| < 0.27
none, r=2 +0.0011 0.0425 0.0545 176 +0.0042 0.0845 0.1121 217
flat, r=2 +0.0039 0.0551 - 176 -0.0035 0.0866 0.1165 218
flat, r=4 -0.0049 0.0450 0.0586 173 -0.0012 0.0843 0.1117 211
flat, r=6 -0.0051 0.0485 0.0656 168 +0.0016 0.0880 0.1200 212
plane, r=2 +0.0041 0.0506 0.0711 178 -0.0053 0.0939 0.1381 208
plane, r=4 -0.0040 0.0444 0.0576 172 -0.0048 0.0862 0.1156 219
plane, r=6 -0.0001 0.0481 0.0647 131 +0.0014 0.0838 0.1107 152

Sky-fitting 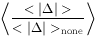fraction
method
none, r=2 1.00
flat, r=2 1.19
flat, r=4 1.17
flat, r=6 1.25
plane, r=2 1.21
plane, r=4 1.14
plane, r=6 1.23

Table 4-2. Observational Scatter on the Main Sequences of 47 Tuc and the SMC
Sky-fitting <Delta> <|Delta|> sigmahatb-v n <Delta> <|Delta|> sigmahatb-v n
method (mag) (mag) (mag) (mag) (mag) (mag)
11.35 < v < 13.03 13.50 < v < 14.74
|Delta| < 0.05 |Delta| < 0.07
none, r=2 -0.0004 0.0137 0.0175 49 +0.0021 0.0174 0.0219 55
flat, r=2 +0.0016 0.0136 0.0173 47 +0.0087 0.0223 0.0299 51
flat, r=4 -0.0025 0.0138 0.0176 47 -0.0039 0.0191 0.0243 53
flat, r=6 -0.0031 0.0137 0.0175 48 -0.0065 0.0202 0.0260 57
plane, r=2 +0.0067 0.0165 0.0227 45 +0.0154 0.0238 0.0338 50
plane, r=4 -0.0025 0.0134 0.0170 46 -0.0057 0.0206 0.0267 52
plane, r=6 -0.0021 0.0132 0.0167 47 -0.0041 0.0205 0.0265 56
14.74 < v < 16.25 15.71 < v < 17.00 (SMC)
|Delta| < 0.17 |Delta| < 0.27
none, r=2 +0.0005 0.0478 0.0612 84 -0.0021 0.0778 0.1002 220
flat, r=2 +0.0145 0.0584 0.0841 71 +0.0009 0.0980 - 198
flat, r=4 -0.0024 0.0523 0.0688 79 -0.0136 0.0878 0.1192 206
flat, r=6 -0.0108 0.0557 0.0761 79 -0.0100 0.0823 0.1078 201
plane, r=2 +0.0095 0.0611 0.1022 75 +0.0085 0.1012 - 194
plane, r=4 -0.0003 0.0594 0.0882 81 -0.0045 0.0794 0.1028 196
plane, r=6 -0.0078 0.0533 0.0707 80 -0.0035 0.0779 0.1003 207

Sky-fitting 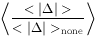fraction CPU time
method (hr)
none, r=2 1.00 12.5
flat, r=2 1.19 16.1
flat, r=4 1.08 16.9
flat, r=6 1.10 20.8
plane, r=2 1.29 19.3
plane, r=4 1.11 17.4
plane, r=6 1.06 21.9

Finally, I would like to show the results of another quickie test I did to see whether the (a, b) weight-fudging scheme I talked about in my third lecture would help any. In one CCD frame, I chose three well-isolated stars of different apparent magnitudes, and performed profile fits on them. Then I simulated a cosmic-ray hit on the image by simply adding a certain brightness increment to that pixel which was closest to the center of the star. I repeated this for "defects" of increasing size, and watched how the derived magnitudes for the three stars changed with different amplitudes for the "cosmic-ray" event. This experiment is represented in the uppermost panel of Fig. 4-7. The brightest star, with an instrumental magnitude of ~ 12, is only about a factor of two fainter than a star which would have saturated the CCD; thus, it is among the brightest stars that one would want to measure. Then there is another star a factor of 10 fainter, with an instrumental magnitude of 14.5; and finally a third star ten times fainter again, with an instrumental magnitude of 17, which is maybe a factor of two brighter than the faintest star you could reliably detect in this image. As you can see, adding arbitrary amounts of flux to these stars makes them all brighter (surprise!), and the faintest star gets brighter faster than the brightest one (surprise, surprise!). As the "cosmic-ray event" get stronger, the magnitude errors grow until the point is reached where the defect crosses over the "maximum good data-value" threshold, and the answer switches abruptly to the best profile fit based on all the pixels within the fitting region except the corrupted one. The other three panels show how the magnitudes resulting from the best fit vary with defect size, for a = 2.5 and b = 2, 4, and 8. As you can see, increasing b reduces the size of the maximum error that a cosmic-ray hit can produce in the photometric result, and it also reduces the size of the discontinuous jump in the derived magnitude that will be produced by a tiny increase in the size of the cosmic ray event (viz., that increment which changes it from a "good" pixel to a "bad" one). For a = 2.5 and b = 8, the maximum error produced by a cosmic-ray hit on the faintest star is only 0.025 mag - and this in a star which is already uncertain by about 0.025 mag because of readout noise and Poisson statistics alone. In my opinion, since we know that the error sources in a CCD image are not strictly Gaussian (cosmic rays, hot pixels, electron traps, flat-field errors, undected stars can all be comparable to or larger than readout noise and photon statistics in individual pixels - especially when many consecutive frames are averaged into one) one should not stand upon arguments of mathematical purity and insist upon cookbook least squares. You'll probably get better answers if your program (gently) withdraws some of its confidence from funny-looking data.

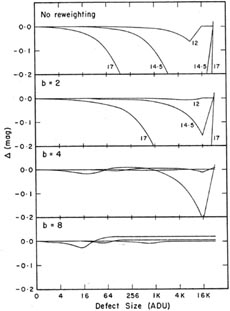
Figure 4-7
Figure 4-7.

This assertion is patently not true when the data are undersampled. When you are trying to determine three or four fitting parameters for a star image which may only occupy four or five pixels, it's foolish to give the computer permission to throw away any pixel it doesn't like. You have to be more subtle here. One possibility is to shade beta toward a value of 1.0, so large residuals don't get ignored, they get medianed. Otherwise, it's probably better to turn the clipping off altogether and accept the fact that you'll get total garbage (as distinguished from partial garbage) for some of your stars. I think that someday there will be a more sophisticated solution, which is this: when multiple exposures of a given field are available, all exposures will be reduced simultaneously. Let's say you've got eight frames of a field, with sampling such that each star occupies, on average, four pixels. Now you've got 32 data points to use in determining the star's 3 unknowns - its (x, y) centroid and its magnitude; 10 unknowns if you think the star may be a variable. Now it's probably safe to throw away cosmic-ray hits. In the best of all possible worlds, the eight frames would be subject to arbitrary translations and rotations with respect to one another: that keeps the star from always falling on the same detector flaws, and it gives new information on exactly what the star's position is by sampling the profile a little differently each time. Now you've got 35 new unknowns - the four transformation constants that relate the coordinate systems of each of frames 2, ... , 8 to that of frame 1 (see Lectures 1 and 5), and the one constant to relate the photometric zero point of each of the subsequent frames to the system of the first - but there are N stars in the field! You've got 4 x N x 8 observations (four pixels per star per frame to solve for 3N + 35 unknowns (plus an additional 7 magnitudes for each of the suspected variable stars) - you're gloriously overdetermined!

6 Actually, you can fit the local sky brightness with more than one parameter, and some software packages routinely do. For instance, if your stars are in a globular cluster or superimposed on an elliptical galaxy or something, you can replace B with B0 + Bx(x - x0) + By(y - y0), and solve for the three parameters B0, Bx, By, thereby fitting a least-squares plane to the background. There's no theoretical reason why you have to stop here; if the data were good enough you could fit polynomial surfaces of arbitrary order, or segments of Hubble laws, or whatever you like. Back.

Next Contents Previous