


In order to make a comparison between the models and data, we have
considered line ratios, involving the following most intense emission
lines observed in the spectra of Seyfert 2's and LINERs: [O II]
 3727,
[O III]
3727,
[O III] 
 4959, 5007, [N II]
4959, 5007, [N II]

 6548, 6584, and [S II]
6548, 6584, and [S II] 
 6717, 6731.
6717, 6731.
To begin, we have used the ratio I
( 6717) /
(
6717) /
( 6731) in order to
obtain an estimate for the gas density. As is well-known (e.g.,
Osterbrock 1974),
this ratio is sensitive to the density between the
limits 102 and 104-105
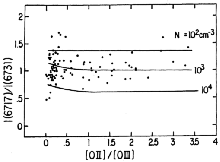
cm-3. So we have plotted, in Figure 1, this
ratio for the observational data and the above-described
photoionization models, with the slope of the ionizing continuum
6731) in order to
obtain an estimate for the gas density. As is well-known (e.g.,
Osterbrock 1974),
this ratio is sensitive to the density between the
limits 102 and 104-105
cm-3. So we have plotted, in Figure 1, this
ratio for the observational data and the above-described
photoionization models, with the slope of the ionizing continuum
 =
-1.5 (see below) and gas density in the above range. From the
distribution of points in Figure 1
it can be concluded that, in most
objects, the gas producing [S II] has densities in the range
102-104 cm-3.
=
-1.5 (see below) and gas density in the above range. From the
distribution of points in Figure 1
it can be concluded that, in most
objects, the gas producing [S II] has densities in the range
102-104 cm-3.
|
Figure 1. The density-sensitive ratio I
( |
Using this range of densities, we have calculated models with the
slope  having three values: -1,
-1.5, and -2. The best agreement with
the data was obtained for
having three values: -1,
-1.5, and -2. The best agreement with
the data was obtained for  =
-1.5. The behavior of the models for
=
-1.5. The behavior of the models for
 =
-1 and -2 is discussed at the end of this section. We remark that a
slope
=
-1 and -2 is discussed at the end of this section. We remark that a
slope  = -1.5 was also used by
previous authors (e.g.,
Ferland and Netzer 1983)
for nonthermal photoionizing sources. Even for the
alternative scenario of WARMERs
(Terlevich and Melnick
1985),
it is shown that the integrated ionizing spectrum is similar, in the
ultraviolet region, to a power-law spectrum with slope
= -1.5 was also used by
previous authors (e.g.,
Ferland and Netzer 1983)
for nonthermal photoionizing sources. Even for the
alternative scenario of WARMERs
(Terlevich and Melnick
1985),
it is shown that the integrated ionizing spectrum is similar, in the
ultraviolet region, to a power-law spectrum with slope
 = -1.5.
= -1.5.
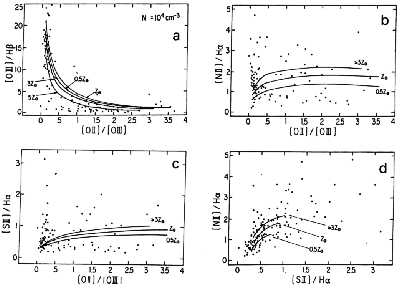
We have constructed four diagrams, involving the strongest emission
lines: [O III] / H x [O II]/[O III], [N II] /
H
x [O II]/[O III], [N II] /
H x [O II]/[O III],
[S II]/H
x [O II]/[O III],
[S II]/H x [O II] / [O III],
and [N II] / H
x [O II] / [O III],
and [N II] / H x [S II] /
H
x [S II] /
H . We have plotted in
Figures 2a-d the data and models with
. We have plotted in
Figures 2a-d the data and models with
 = -1.5, densities
102, 103,
and 104 cm-3 and ionization parameter (U) varying
in the range 10-2.5 to
10-4. This range of U is necessary in order to reproduce the
[O II] /
[O III] values presented by the data. The abundances are solar for all
the elements. We show also the shock models mentioned in the previous
section. From the diagrams in Figure 2 we obtain
the following results.
= -1.5, densities
102, 103,
and 104 cm-3 and ionization parameter (U) varying
in the range 10-2.5 to
10-4. This range of U is necessary in order to reproduce the
[O II] /
[O III] values presented by the data. The abundances are solar for all
the elements. We show also the shock models mentioned in the previous
section. From the diagrams in Figure 2 we obtain
the following results.
(1) The shock models do not reproduce most of the data; they could only reproduce the data with an [O II]/[O III] ratio larger than 2.5, but most observational points present smaller values for this ratio.
(2) In order to cover the data in the diagram [O III] /
H x [O II] /
[O III] it is necessary to consider the presence of clouds of densities
higher than 104 cm-3. It can be seen that models
with densities between
104 and 105 cm-3 reproduce most of the
data. This higher density for
the clouds producing [O III] can be understood considering that
emission is enhanced in the higher density clouds, as long as the
density remains lower than the critical value (7.0e5 cm-3 for
[O III]). In fact, the observed correlations between the FWHM of the
emission lines and their critical densities (e.g.,
Storchi-Bergmann, Bica,
and Pastoriza 1990;
Filippenko and Sargent
1988)
indicate the
presence of clouds of different densities in the narrow-line region of
active galactic nuclei.
x [O II] /
[O III] it is necessary to consider the presence of clouds of densities
higher than 104 cm-3. It can be seen that models
with densities between
104 and 105 cm-3 reproduce most of the
data. This higher density for
the clouds producing [O III] can be understood considering that
emission is enhanced in the higher density clouds, as long as the
density remains lower than the critical value (7.0e5 cm-3 for
[O III]). In fact, the observed correlations between the FWHM of the
emission lines and their critical densities (e.g.,
Storchi-Bergmann, Bica,
and Pastoriza 1990;
Filippenko and Sargent
1988)
indicate the
presence of clouds of different densities in the narrow-line region of
active galactic nuclei.
(3) The [O II] / [O III] and [O III] /
H ratios are
strongly dependent on the ionization parameter U.
ratios are
strongly dependent on the ionization parameter U.
(4) The ratios [N II] / H and [S
II] / H
and [S
II] / H depend only weakly on the
density and U. Model sequences for N = 10-5
cm-3 were not plotted in the
corresponding diagrams for the sake of clarity; The values become
lower due to collisional deexcitation and superpose with some of the
other values. It is not possible, by varying only U and
Ne to
reproduce the range of values presented by the ratios [N II] /
H
depend only weakly on the
density and U. Model sequences for N = 10-5
cm-3 were not plotted in the
corresponding diagrams for the sake of clarity; The values become
lower due to collisional deexcitation and superpose with some of the
other values. It is not possible, by varying only U and
Ne to
reproduce the range of values presented by the ratios [N II] /
H and
[S II] / H
and
[S II] / H .
Figure 1d shows that
the [N II] / H
.
Figure 1d shows that
the [N II] / H x [S II] /
H
x [S II] /
H relation can be
in part reproduced by varying U; nevertheless, we have plotted, for
the different densities, the U range which reproduces the range of the
[O II] / [O III] ratios. Higher U values would give [O II] / [O III]
ratios which do not correspond to the data. So it is necessary to vary
another parameter to reproduce the range of [N II] /
H
relation can be
in part reproduced by varying U; nevertheless, we have plotted, for
the different densities, the U range which reproduces the range of the
[O II] / [O III] ratios. Higher U values would give [O II] / [O III]
ratios which do not correspond to the data. So it is necessary to vary
another parameter to reproduce the range of [N II] /
H and [S II] /
H
and [S II] /
H values.
values.
|
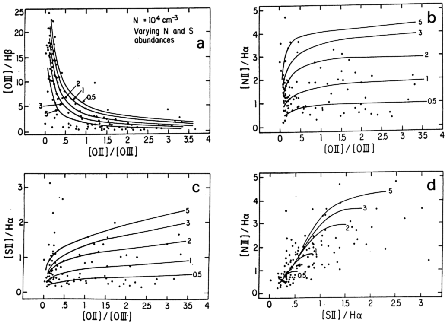
Figure 3a-d. Sample galaxies (dots) and photoionization models (lines) for gas density 104 cm-3 and varying metallicity in the same diagrams as Figure 2. |
In order to obtain a larger range in the model values of [N II] /
H and [S II] / H
and [S II] / H , we computed
models with metallicities half-solar and
three and five times solar. These models, together with the solar
abundance model and the data points, are plotted in
Figures 3a-d. For
clarity we have fixed the density as N = 104
cm-3. The results which
can be obtained from this set of models are:
, we computed
models with metallicities half-solar and
three and five times solar. These models, together with the solar
abundance model and the data points, are plotted in
Figures 3a-d. For
clarity we have fixed the density as N = 104
cm-3. The results which
can be obtained from this set of models are:
(1) Comparing Figure 3a to
Figure 2a, it can be seen that the effect
of a higher metallicity in the gas in the diagram [O III] /
H is
equivalent to the effect of a higher density. A higher metallicity
lowers the temperature-sensitive ratio [O III] /
H
is
equivalent to the effect of a higher density. A higher metallicity
lowers the temperature-sensitive ratio [O III] /
H due to the cooling
of the gas produced by the forbidden line emission. It can be seen
that the data on this diagram are compatible with a higher metallicity
in the nuclear gas.
due to the cooling
of the gas produced by the forbidden line emission. It can be seen
that the data on this diagram are compatible with a higher metallicity
in the nuclear gas.
(2) In the diagram [N II] /
H x [O II] / [O III] it can be
seen that the
models can reproduce part of the vertical dispersion of the data, but
not all. In particular, we note that the sequence for metallicity
three times solar is an upper limit for the [N II] /
H
x [O II] / [O III] it can be
seen that the
models can reproduce part of the vertical dispersion of the data, but
not all. In particular, we note that the sequence for metallicity
three times solar is an upper limit for the [N II] /
H ratio; The
sequence for metallicity five times solar gives lower values than
these. So, a varying abundance for all the elements does not reproduce
the range of[N II] /
H
ratio; The
sequence for metallicity five times solar gives lower values than
these. So, a varying abundance for all the elements does not reproduce
the range of[N II] /
H ratios presented by the data.
ratios presented by the data.
(3) A varying metallicity also does not reproduce the range presented
by the [S II] / H ratios nor the
relation [N II] / H
ratios nor the
relation [N II] / H x [S II] /
H
x [S II] /
H .
.
|
Figure 4a-d. Same diagrams as Figures 2 and 3 for model with simultaneous variation of sulfur and nitrogen abundances from 0.5 to 5 times solar. The other elements have solar abundance. |
The next step we have tried was to vary only the abundances of nitrogen and sulfur, keeping the abundance of the other elements at the solar value. We have computed models for nitrogen and sulfur with abundances half-solar and two, three, and five times solar. These models, for density N = 104 cm-3, are plotted in Figures 4a-d. It can be seen that:
(1) The result regarding the [O III] /
H x [O II] /
[O III] diagram is
similar to that obtained with the enhancement of all the metals; Due
to the cooling produced by the forbidden nitrogen and sulfur lines,
the [O III] / H
x [O II] /
[O III] diagram is
similar to that obtained with the enhancement of all the metals; Due
to the cooling produced by the forbidden nitrogen and sulfur lines,
the [O III] / H ratio is lowered. So it is possible to reproduce the
data with clouds of density 104 to 105
cm-3 and nitrogen and sulfur
abundances from half-solar to five times solar.
ratio is lowered. So it is possible to reproduce the
data with clouds of density 104 to 105
cm-3 and nitrogen and sulfur
abundances from half-solar to five times solar.
(2) The data points in the [N II] /
H x [O II] / [O III] diagram are well
covered by these models. The lowest points can be reproduced by models
with the same abundances and densities 102-103
cm-3 (see Fig. 2b).
x [O II] / [O III] diagram are well
covered by these models. The lowest points can be reproduced by models
with the same abundances and densities 102-103
cm-3 (see Fig. 2b).
(3) The data in the [S II] /
H x [O II] / [O III] and [N II]
/ H
x [O II] / [O III] and [N II]
/ H x
[O II]/[O III] diagrams are also much better reproduced by this set of
models. It is not possible to reproduce the data on the last diagram
by varying only the abundance of N or S; it is necessary to vary the
abundances of both elements together.
x
[O II]/[O III] diagrams are also much better reproduced by this set of
models. It is not possible to reproduce the data on the last diagram
by varying only the abundance of N or S; it is necessary to vary the
abundances of both elements together.
A similar analysis to that described above was also done for slopes
of the ionizing continuum  = -1
and
= -1
and  = -2. Both values led to a
worse overall agreement between the model values and the data. In
particular, models for
= -2. Both values led to a
worse overall agreement between the model values and the data. In
particular, models for  = -2 do
not reproduce the observed [O III] /
H
= -2 do
not reproduce the observed [O III] /
H x [O II]/[O III] diagram except for densities lower than 102
cm-3. And,
for these densities, the [N II] /
H
x [O II]/[O III] diagram except for densities lower than 102
cm-3. And,
for these densities, the [N II] /
H and [S II] /
H
and [S II] /
H values can only be
reproduced with higher N and S abundances than that obtained for
values can only be
reproduced with higher N and S abundances than that obtained for
 =
-1.5. Models with
=
-1.5. Models with  = -1 give
higher [S II] /
H
= -1 give
higher [S II] /
H ratios than those
observed, requiring unacceptably low S abundances (< 0.5 solar) in
order to reproduce the data.
ratios than those
observed, requiring unacceptably low S abundances (< 0.5 solar) in
order to reproduce the data.