3. QUANTITATIVE CLASSIFICATIONS

3.1 Luminosity Distribution Laws: Photometric Parameters

Detailed surface photometry confirms the validity of one of the two basic Hubble classification criteria, namely that the luminosity of normal galaxies can be resolved into two principal components:

(I) a spheroidal component characteristic of elliptical galaxies (de Vaucouleurs 1948, 1953, 1959, 1962; Fish 1964; King 1962, 1966), of the bulge of lenticulars (de Vaucouleurs 1959-1975; Tsikoudi 1977) and early spirals Sa, Sb (de Vaucouleurs 1958b, van Houten 1961), and even of other Population II samples such as the system of globular clusters (de Vaucouleurs 1977d),

(II) a flat component characteristic of the disks of spirals Sb-Sd (de Vaucouleurs 1958b, 1959, 1974; Freeman 1970; Schweizer 1976) and of magellanic irregulars Sm-Im (Ables 1971; de Vaucouleurs and Freeman 1972).

In reduced units (* = r* / r*_e, J = I/I_e) the mean surface brightness distribution in near face-on systems is well represented by

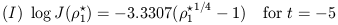
(14)

and

(15)

or by a linear combination for intermediate types. In a first approximation the relative integrated luminosity curves

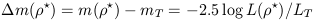
(16)

form a one-parameter family as a function of type t (see Fig. 5 in RC2).

The total luminosity of the spheroidal component is

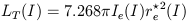
(17)

and that of the flat component

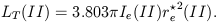
(18)

The fraction K_I = L_T(I) / L_T of the total luminosity L_T = L_T(I) + L_T(II) which is contributed by the spheroidal component is, therefore, also a function of t and a quantitative measure of the first Hubble classification criterion.

From a study of available photometric data for 24 galaxies, Yoshizawa and Wakamatsu (1975) found that L_T(I) / L_T(II) = K_I / (1 - K_I) varies with t as shown in Fig. 20 and that the absolute magnitude of the spheroidal component is loosely correlated with while the absolute magnitude of the disk component is essentially independent of t [but varies with M°_T at t = const. as noted by Freeman (1970)].

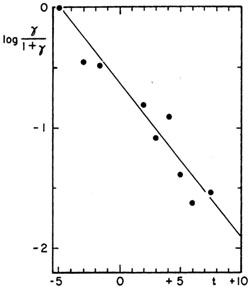
Figure 20. Correlation between mean bulge/disk luminosity ratio = LT(I) / LT(II) and morphological type t, after Yoshizawa and Wakamatsu (1975). Note KI = / (1 + ) is the bulge fractional luminosity LT(I) / LT.

This leads to a first quantitative 2-parameter classification system using K_I (or ) as a type indicator of the bulge/disk ratio and L_T = L_T(I) / K_I as luminosity indicator. ⁽⁴⁾

A second, more refined 3-parameter scheme rests on the fact that for L_T = 1, the two-component model has 2 free parameters = r*_e(I) / r*_e(II) and = I_e(I) / I_e(II), the ratios of the effective radii and specific intensities of the spheroidal and flat components which determines as before the bulge/disk ratio = 1.91 ² . The 3rd parameter may be L_T or a scale factor, say r*_e for the whole galaxy. This scheme allows also for large vs. small, as well as bright vs. faint bulges and disks, all of which are observed in various combinations, although observational selection effects may conspire to restrict to a small range the bulge or disk parameters currently available; this in turn may produce deceptively tight correlations.

Work is in progress to apply this photometric classification scheme to several hundred galaxies with adequate photographic and photoelectric data.

Remark: For galaxies with a nuclear source, e.g. Seyfert galaxies, the same scheme is applicable after subtraction of the (often variable) contribution of the quasi-stellar source (see de Vaucouleurs 1973, de Vaucouleurs et al. 1973), that is

3.2 Color Distribution Laws: Colorimetric Parameters

Integrated color indices C(*) = B(*) - V(*) are available for ~ 1000 galaxies (and for several hundreds in U - B); the average color-aperture relations C(, t) where = log A / A_e is the normalized aperture (A_e = aperture transmitting half the total B flux) have been derived for all the major morphological types t (see Fig. 6 in RC2). In principle, the total color indices C^o_T (Section 2.2) and the color amplitude C_T = C_N - C_T, where C_N = C( << -1) is the nuclear color, could define an equivalent type t. However, the variable effects of line emission, inclination (absorption) and the intrinsic (cosmic) color range at t = const. does not make this approach a promising one.

Also, attempts at establishing a color-magnitude diagram for galaxies have been frustrated by the lack of correlation between color and luminosity at t = const.; as noted in Section 2.2 a weak correlation appears only when all late-types (Sc to Im) are dumped into the original Sc Hubble class.

At present broad-band colors do not appear promising as a basis for a quantitative classification scheme, unless supplemented by detailed spectral data. Emission-free colors measured through narrow-band filters are more promising, but are not yet precise and numerous enough to be a practical alternative at this time.

3.3 Kinematical Parameters

The empirical observations that (1) V_M is a function of t and L, i.e., of (Fig. 19b), and (2) 2R_M / D₀ is a function of t, i.e., of the bulge/disk ratio (Fig. 19c) could be used to set up a kinematical classification scheme with _M = log 2R_M / D₀ serving as a type indicator and _M = log V_M as luminosity indicator; however, R_M is too poorly defined and measured to make this scheme practical.

A variant uses the centrifugal force at R_M, K_M = V²_M / R_M as a type indicator (Fig. 21a, b) (Wakamatsu 1976). This has the disadvantage that its 2 parameters K_M and _M are not independent, leading to a deceptively tight correlation which is mainly a result of systematic errors in R_M.

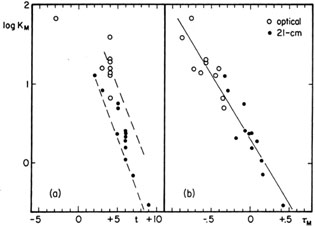
Figure 21. Correlations between centrifugal force KM at RM, and morphological type t (a) and normalized radius M (b), after Wakamatsu (1976).

3.4 Dynamical Parameters

Basic dynamical parameters such as total mass

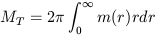
(19)

and total angular momentum

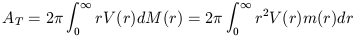
(20)

where m(r) = projected surface density, have been proposed as elements of a more fundamental classification scheme (Wakamatsu 1976). However, the two parameters are not independent and are poorly defined by the observations because a large fraction of the angular momentum is in the outer regions of disk galaxies (at r >> where R_M) where V(r) and m(r) are essentially unknown (Nordsieck 1973).

In particular, the tight correlations reported between M_T and A_T (Wakamatsu 1976, see de Vaucouleurs 1974 for earlier references) are largely trivial (Freeman 1970, Nordsieck 1973). The only significant difference that seems well established is that ellipticals and lenticulars have smaller specific angular momenta (i.e., per unit mass) than do spirals (Bertola and Capaccioli 1975, 1977). However, this marginally detectable difference is not a practical classification criterion.

A better scheme involves M_T and a mass distribution parameter ' which depends on the bulge/disk ratio (Wakamatsu 1976), assuming that bulge and disk are each characterized by a constant M / L = f ratio; thus if M_I = ' M_II, ' = f_I L_I / f_II L_II, and M_II = 2 S₀ / ² is the mass of the exponential disk (Freeman 1970)

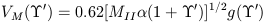
(21)

and

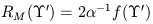
(22)

where f('), g(') are numerical factors depending on the mass distribution within the bulge. ' = (f_I / f_II) is essentially a morphological type indicator strongly correlated with K_M = V²_M / R_M. This scheme provides a dynamical interpretation of the (T, L) empirical system, but again is hardly a practical classification system in view of the current scarcity of reliable photometric and dynamical data. ⁽⁵⁾

3.5 Physical Parameters

Another quantitative classification system could be based on fundamental physical parameters such as total mass M_T and the gas/stars ratio measured by the neutral hydrogen to total mass ratio h = M_H / M_T, since principal component analysis shows that M_H and M_T are correlated, but h and M_T are not (Brosche 1971). However, M_T requires dynamical information and, as noted in Section 3.4, is severely restricted; an acceptable substitute is the total luminosity L_T since f = M_T / L_T is highly correlated with color index C_T, at least for the spheroidal component (Fig. 22) (for details and references see de Vaucouleurs 1974). Similarly h = M_H / M_T which requires M_T and is distance dependent, could be replaced by g = M_H / L_T which is independent of distance; this ratio is measured by the hydrogen index HI as discussed in Section 2.3.

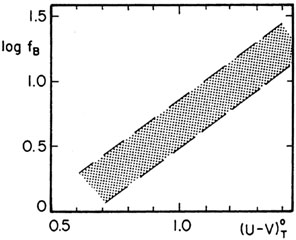
Figure 22. Correlation between mass/luminosity ratio fB = log MT / LB and (U - V)oT color index for spheroidal systems.

⁴ A simplified version of this scheme which makes no assumption on the forms of the luminosity laws would be to use the concentration index C₃₁ as a rough measure of the bulge/disk ratio. Back.

⁵ The same remark applies to the interpretation of luminosity classification and arm/disk ratios (Schweizer 1976) within the framework of the density wave theory (Roberts et al. 1975). Back.