These merger hopes would all be in vain, of course, if the severe kind of dynamical friction which they seem to require proved simply to be unattainable. Fortunately, as this section will now review, such pessimism seems unwarranted for slow and deeply interpenetrating encounters. It remains quite a different story, however, with making sure that two disk systems in some more grazing passage necessary to produce impressive tails can actually stop and merge rapidly enough - i.e., leave those tails still neatly in view when the bodies sink together. No one seems yet to have made any progress worth citing on this second and more pertinent question of dynamics.
Still, to be grateful for what we have got, it is clear now that simply the splash or "violent relaxation" from mutual tidal forces can indeed halt rapidly any two comparable and already spherical stellar systems which happen to blunder head-on through each other with only about the speed developed in free fall from rest at infinity. Better yet, it appears that already the "impulsive tide" approximation of Alladin (1965; see also Sastry and Alladin 1970, 1977) - which in effect extended Chandrasekhar's friction estimates to the very nonuniform situations arising when whole galaxies interpenetrate at high speed - provides a neat and at least semi-quantitative explanation of even this near-parabolic stickiness.
The examples offered by Alladin and Sastry themselves refer mostly to (spherical) mass distributions akin to the classical n = 4 gaseous polytrope. To appreciate the gist of their reasoning, however, it seems preferable to concentrate instead on the n = 5 polytrope known either as the Schuster or the Plummer model. Its volume density is given by the well-Known formula
where M is the total mass, a is a scale, length, and r is the
spherical radius. The equally simple force law
of this model greatly reduces the chore of calculating the lateral speed
that a test particle would develop upon rushing past it at distance D,
with an immense and nearly constant speed U. And also for this model,
it is pleasant to reckon further that if instead of a single particle
the passerby consisted of many different stars from an identical
system traveling with a (supposedly) constant speed U along an exactly
head-on straight trajectory, then the tidally-induced motions
v
soaked up suddenly by that intruding galaxy.
Alladin and Sastry stressed very properly that such a gain of
internal energy can occur only at the expense of the energy of
relative motion of the two galaxies. In essence, they said, any such
inward splash converts some of that orbital energy into mere
stellar-dynamical heat. The only awesome thing about this reasoning is
the magnitude of that expected transfer. To assess it quickly, notice
that the potential energy released in bringing two undeformed and yet
penetrable Plummer models together from infinity to a perfectly
superposed state is |W| = (3
For other polytropes n = 4, 3, and 2, incidentally, laborious
numerical integrations (such as Alladin and Sastry were also forced to
perform) yield very similar ratios of 46.3, 45.6, and 45.1 per cent.
These striking conclusions can, of course, be faulted for abusing
the impulsive and constant-speed assumptions on which they were based.
Strictly speaking, it is correct to treat such estimates as merely
asymptotic - that is, to infer only that a head-on intrusion of equal
n = 3 polytropes, for example, with relative speeds U >> Uesc, will
cost that pair a multiple
of their new and much larger peak kinetic energy. As such a former
skeptic, however, I must say that I now regard Equations (5) and (6)
as very adequate even when mistreated. What convinced me was not the
occasional mergers found by Hohl, Miller and/or Prendergast in their
planar 105 -body experiments; it was more the 3-D studies with 100
rings or 2000 mass points described below.
Figure 2 updates the brief report by
Toomre (1974)
on a numerical
experiment in which Larry Cox and I simulated each of two
parabolically approaching Plummer models as a beehive of
randomly-moving coaxial rings, all interacting with one another via
gravity forces softened modestly at close range. Our aim in using
these softened rings instead of conventional point masses was to
reduce greatly all inter-particle relaxation effects (such as were
blamed, perhaps unduly, by
Aarseth and Hills 1972
in their own
experiment). We wished to concentrate more on the commotion due to the
sudden onset of the collective tidal forces. The old diagram gave
results for 12+12 rings. Figure 2, nearly as
ancient, now repeats the
exercise with 50+50. In units of the Plummer scale length a, it shows
the axial coordinate z of each ring as a function of time t. One small
discordant note: the densest cores in this diagram seem to separate as
far as
Figure 2. Head-on impact and merger of two
equal Plummer models that
arrived with escape speed. The axial coordinates z(t) of one set of 50
softened rings used to represent one such model are shown dotted, the
others as solid curves.
Figure 3 was contributed very kindly by
van Albada and van
Gorkom (1977),
as a cousin of an impressive test case already shown in their
paper. As if only for variety, it refers to polytropes of index n = 3
- and these were now assigned, at infinity, a relative motion U =
Uesc / 2
Figure 3. Head-on impact and merger of two
stellar dynamical n = 3
polytropes upon arrival at center with 1.061 times the escape speed
Uesc. This diagram by van Albada and van Gorkom shows projected
densities at seven instants.
It will not have escaped the reader that, unfortunately, this little
success story has referred only to (already) spherical systems taking
part in the most symmetric encounters imaginable. As regards disks and
their own interplay, it is trivial, of course, to extend both this
thinking and the experiments to exactly axial (= face-to-face)
penetrations of two very flattened assemblies of rings. And by
constraining them to remain axisymmetric, one can even ignore blithely
all serious instability questions of the subject. My own experience in
that tractable but unrealistic setting has been that while the
immediate energy loss runs only around 20 per cent (instead of the
high 40s) for a variety of disk models, soon enough they manage to
merge also, and they tend to yield outlines (though hardly the full
density profiles) resembling E3/E4 galaxies. But all this, I stress
again, seems almost irrelevant. It is surely no substitute for the
much more difficult studies of off-center impacts of stable
self-gravitating disks or, more likely, disk-halo systems. Quite
understandably, such studies have been very slow to emerge.
To conclude, the big worry remains that the strength of braking may
drop off too rapidly with increasing impact parameter or miss
distance, as one seeks circumstances that will also permit the
manufacture of tails of the sort summarized in
Table 1. Certainly, the
off-axis studies of Alladin and Sastry convey the same warning even
for encounters of spheres; paraphrasing them again, it seems that the
center of one galaxy needs to impact the other system no farther out
than about the 1/2 or 3/4-mass radius, lest the rapidity of their
sinking cease to be impressive. Ironically, there is apt to be one
logical "out" even if it emerges that disk models cannot decelerate
fast enough on their own; In principle at least, one can always embed
them, prior to any fateful encounter, within some appreciably larger
and more massive systems like the much-discussed extensive halos. Such
outer parts would by definition interpenetrate and even splatter
nicely as those visible disks only graze one another. But what a
strange way that would be to make ellipticals!
This work was supported in part by a generous grant from the
National Science Foundation.
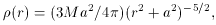
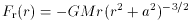
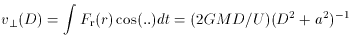
of
those stars toward that orbit axis would amount to a kinetic energy
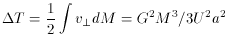
/16)
(GM2/a). Of course this equals not
only the negative sum of the potential energies of the two systems
reckoned individually while still far apart, but also the "orbital"
kinetic energy MUesc2/4 developed by those two
when overlapping at the
very bottom of a (rigid) free fall from rest at great distance. Now
suppose both models indeed to be flabby for the purposes of Equation
(4), and adopt as the speed U the full relative escape speed
Uesc that
we just estimated. It then follows at once that the ratio of the lost
to the available kinetic energy is fully
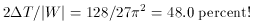
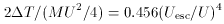
z = 8a after the first
transit, whereas two rigid n = 5
polytropes like here should not even have reached 4a after a presumed
48 per cent loss of kinetic energy at their instant of overlap. At
least half this discrepancy, however, seems due to our reduction of
the near-gravity.
2 = exactly
the root-mean-square internal speed. Owing to 2000
particles an d more accurate treatment of the gravity,
Figure 3 is
much to be preferred technically to
Figure 2. Its chief immediate
value, however, lies doubtless in this explicit demonstration that
even a moderately hyperbolic initial motion does not yet spoil the
merger. Of course, the total energy just ceases to be negative if we
double the speed at infinity from the value in
Figure 3. At least such
a recipe no longer promises a merger - and further experiments quite
agree. In fact, van Albada (1976, private communication) reckons
empirically that captures cease already when U(0)
1.15 Uesc. By
contrast, Equation (6) patterned upon Alladin's work places that
crossover at just a shade under 1.16 Uesc Not bad for a simple
formula.
