Once having identified the specific nuclear chronometers (in this case the r-process nuclei 232Th, 238U, and 235U) for dating the epoch of galactic nucleosynthesis, further critical input astrophysical quantities include:
Abundance determinations for the thorium and uranium isotopes of interest are provided by analyses of meteoritic material. The situation for the 232Th-238U pair is complicated by the chemical differences between the two elements. Anders & Ebihara (1982) and Anders & Grevesse (1989) found the present day value of Th/U to be 3.6, which translates into a primordial solar system ratio (232Th / 238U)SS = 2.32. This is the value we have adopted for this paper. We have also used the ratio (235U / 238U)SS = 0.317 provided by these authors.
The determination of the production ratios (232Th /
238U)r-process and (235U /
238U)r-process resulting from r-process
nucleosynthesis is, in general, a sensitive function
of both the input nuclear physics and the physical conditions under
which the r-process proceeds
(Kratz et al. 1993,
1994).
There are considerable uncertainties associated with
the nuclear properties of the unstable neutron-rich progenitors of the
uranium and thorium isotopes of interest. For purposes of illustration,
Table 2 (adapted from the review
articles of Cowan, Thielemann, & Truran
(1991a,
b))
lists representative values for these
production ratios as determined by the indicated references. Note
specifically that the
predicted production ratios span a broad range: 1.40
(232Th /
238U)r-process
1.90 and
0.89 (235U /
238U)r-process
1.89. In general, the final
abundances of these long lived
isotopes involve summations over the abundances of a number of
short-lived progenitors
in alpha decay chains, with the number of progenitors being constrained
by the occurrence
of spontaneous fission at high masses. The effective numbers of
progenitors arrived at by such considerations are 5.8, 6, and 3.35, for
the isotopes 232Th, 235U, and 238U,
respectively. If one assumes that the various progenitors are produced
in equal abundances in the r-process, these numbers may be used directly to
provide a crude estimate
of the production ratios of these isotopes: 232Th /
238U) = 1.73 and 235U /
238U = 1.79.
These values are also included in Table 2 as
identified by `equal abundances assumed.'
In our subsequent discussions, we have adopted the values
(232Th / 238U)r-process = 1.65
± 0.20 and (235U / 238U)r-process
= 1.35 ± 0.30, which represent averages of the values
presented in the Table 2.
One additional factor should be emphasized here. For many other possible chronometers, dating is complicated by the fact that either the parent or the daughter can be formed by more than one astrophysical process - e.g., the 'mixed' r- and s-process chronologies noted in the previous section. The fact that the three radioactive isotopes with which we are concerned - 232Th, 235U, and 238U - are formed in a single astrophysical process lessens the effects of uncertainties in models of galactic evolution and allows improved and more secure estimates to be obtained of their relative levels of production.
The additional input required for dating is the nucleosynthesis history. The basic equations governing the time evolution of the abundance of a radioactive nuclear species are straightforward. In the following, we follow the notation of Tinsley (1980; see, also, Cowan, Thielemann, & Truran 1991a, b). Assuming a homogeneous ISM and instantaneous return of the products of stellar nucleosynthesis into the surrounding gas, the time evolution of species Ni can be written
| 232Th / 238U* | 235U / 238U | Reference |
| 1.65 | 1.42 | Fowler (1972) |
| Truran & Cameron (1971) | ||
| 1.90 | 1.89 | Seeger & Schramm (1970) |
| 1.70 | 0.89 | Wene & Johanson (1976) |
| 1.80 | 1.42 | Fowler (1977) |
| 1.90 | 1.50 | Symbalisty Schramm (1981) |
| 1.50 | 1.10 | Krumlinde et al. (1981) |
| 1.40 | 1.24 | Thielemann et al. (1983a,b) |
| 1.71 | 1.34 | Fowler (1987) |
| 1.60 | 1.16 | Cowan et al. (1987) |
| 1.53 | 1.26 | Thielemann et al. (1989) |
| 1.73 | 1.79 | Equal abundances assumed |
* The r-process calculations of Kratz and Thielemann (1996) yield values for 232Th / 238U ranging from 1.37 to 2.18, depending upon the choice of atomic mass formula. | ||
|
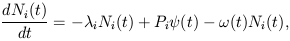
where 
(t) represents the gain
or loss of mass due to accretion and winds,
(t) is the rate
of conversion of mass into stars,
i is the decay
rate of species i, and Pi is the production
rate of species i, per unit mass going into stars. This equation has the
general solution
|
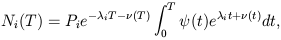
where
|
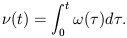
The astrophysical input to these equations then involves the rate of
formation of the
range of stellar masses within which r-process nucleosynthesis
occurs. While calculations
of r-process nucleosynthesis have been carried out for a variety of
plausible astrophysical sites (see, e.g., the reviews by
Hillebrandt 1978;
Schramm 1982;
Mathews & Ward 1985;
and Cowan,
Thielemann, & Truran 1991a),
a firm identification of the appropriate
environment has become possible only recently. Observations of heavy
element abundance
patterns in metal deficient halo stars, described in the next section,
point strongly to the
identification of r-process nucleosynthesis with the environments
provided by the
evolution of massive stars and supernovae of Type II. In this context,
the most promising
mechanism of r-process synthesis would appear to be that associated with
the neutrino
heated "hot-bubble" supernova ejecta
(Woosley & Hoffman
1992;
Meyer et al. 1992;
Takahashi, Witti, &
Janka 1994),
although an r-process associated with the decompression
of cold neutron matter from neutron star mergers
(Lattimer et al. 1977)
provides a viable alternative. An important consequence of the
identification of the r-process with
such massive stars (M 
10
M
) of short lifetimes
(
108 years),
as discussed in the
next section, is that we can reasonably expect that the age we determine
from r-process
chronometer studies is indeed representative of the age of the Galaxy itself.