1998 saw the first plausible, complete accounting of matter and energy in the Universe; a precision determination of the density of ordinary matter; and other strong evidence supporting the basic tenets of Inflation + Cold Dark Matter (CDM). If subsequent data and observations confirm and strengthen the case, I believe we will ultimately refer to 1998 as a turning point in cosmology as important as 1964.
As discussed by Silk, the small variations in the CMB temperature
across the sky have the potential to determine the geometry of
the Universe and thereby  0, the fraction of critical
density contributed by all forms of matter and energy. [Note,
the curvature radius of the Universe and
0, the fraction of critical
density contributed by all forms of matter and energy. [Note,
the curvature radius of the Universe and  0 are related
by, R2curv =
H0-2 / |
0 are related
by, R2curv =
H0-2 / | - 1|, so that
- 1|, so that  = 1
corresponds to a flat geometry,
= 1
corresponds to a flat geometry,  < 1 corresponds to
negatively curved (open) geometry, and
< 1 corresponds to
negatively curved (open) geometry, and  > 1 corresponds
to positively curved (closed) geometry.] In a flat Universe
the differences in temperature between points on the sky are greatest when the
two points are separated by about one degree; in an open
Universe, they are greatest when the separation is smaller than one degree.
The data that now exist indicate that the differences are
indeed greatest on the one-degree scale (see Fig. 1).
More measurements
are being made - from balloons, in Antarctica, and on the
Atacama Plateau in Chile - with definitive measurements to come from
two new satellites: NASA's MAP (launch 2000) and ESA's Planck
Surveyor (launch (2007). If the trend in the results continues,
then we have determined that the Universe is
spatially flat and
> 1 corresponds
to positively curved (closed) geometry.] In a flat Universe
the differences in temperature between points on the sky are greatest when the
two points are separated by about one degree; in an open
Universe, they are greatest when the separation is smaller than one degree.
The data that now exist indicate that the differences are
indeed greatest on the one-degree scale (see Fig. 1).
More measurements
are being made - from balloons, in Antarctica, and on the
Atacama Plateau in Chile - with definitive measurements to come from
two new satellites: NASA's MAP (launch 2000) and ESA's Planck
Surveyor (launch (2007). If the trend in the results continues,
then we have determined that the Universe is
spatially flat and  = 1.
= 1.
These same measurements of the temperature variations of the CMB temperature across the sky also provide important information about the matter inhomogeneities that seeded all the structure we see in the Universe today. Recall, that as Silk explained, the pattern of hot and cold spots on the microwave sky arises due to the lumpy distribution of matter, and in this way the CMB is a snapshot of the Universe at 300,000 years after the beginning (CMB photons come directly to us from their last scattering at this time). The first mapping of the distribution of matter in early Universe using the CMB was done by NASA's COBE satellite (Smoot et al. 1992); since then, many other experiments, with better angular resolution, have ``enhanced the picture.'' At present, the pattern of hot and cold spots indicate, though do not yet prove, that the primeval lumpiness had the following characteristics: Gaussian fluctuations in the curvature of the Universe with an approximately scale-invariant spectrum (see Fig. 1). This is precisely what inflation predicts.
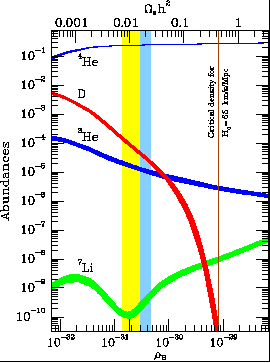
Of the four light elements made in the big bang, the yield of deuterium is most sensitive to the density of ordinary matter (baryons), and for that reason David Schramm and I nicknamed it ``the baryometer'' (Schramm & Turner 1998). Deuterium is also ``very fragile,'' easily destroyed by nuclear reactions in stars. The abundance of deuterium in our local neighborhood has been known for more than twenty years, but because about half of the material around us has been through stars, we cannot interpret the locally measured abundance as the primordial, big-bang abundance. This year, David Tytler and Scott Burles (Burles & Tytler 1998a, b) measured the deuterium abundance in very distant hydrogen clouds. Because these clouds are so distant, we are seeing them at an early time, before stars have destroyed their deuterium. Their measurement of the primeval deuterium abundance pegs the contribution of ordinary matter to be 5% of the critical density (for a Hubble constant of 65 km s-1 Mpc-1), with a precision of better than ± 0.5% (see Fig. 2).
|
Figure 2. Predicted abundances of 4He, D, 3He, and 7Li (relative to hydrogen) as a function of the density of ordinary matter (baryons). The full band denotes the concordance interval based upon all four light elements that dates back to 1995. The darker portion highlights the determination of the density of ordinary matter based upon the recent measurement of the primordial abundance of deuterium (Burles & Tytler 1998a, b), which implies that ordinary matter contributes 5% of the critical density. |
In addition to pinning down the amount of ordinary matter, the Tytler - Burles measurement has allowed us to determine the total amount of matter, using a very clever technique pioneered by Simon White and his colleagues (White et al 1993). They argue that clusters of galaxies, by virtue of their large size (tens of millions of light years in size and thousands of galaxies in number), represent a fair sample of matter in the Universe. Thus, the ratio of baryons to matter in clusters, together with the big-bang determination of the average density of baryons in the Universe serve to pin down the average matter density in the Universe:
Most of the baryons in clusters exist in the form of hot, x-ray
emitting gas and the intensity of x-ray emission allows a determination
of the amount of ordinary matter. The total cluster mass can be
determined in a number of ways: by direct mapping of the
mass by gravitational lensing, by measuring the x-ray temperature,
and by measuring the random
motion of galaxies; all three give the same answer.
The ratio of baryons to matter has been determined
to be 13% ± 1.5%. This implies that matter contributes 40% ± 10%
of the critical density. (Other determinations of the matter density
indicate a similar value.)
The determination that matter contributes 40% of the
critical density has two implications. First,
as Silk discussed, most of the
matter in the Universe is not the stuff we are made out of, which
follows from the inequality,
The second, equally profound implication follows from
the inequality,
This requires further explanation:
According to Einstein's theory of general relativity, the source
of gravity is energy density + three times the pressure (Note:
matter and energy are equivalent, related by E =
mc2; Newton's
theory of gravity holds that the source of gravity is matter alone.)
If the pressure is sufficiently negative - and it must be if
the additional component is to remain smooth - its gravity is
repulsive! Because there is so much of this ``funny'' energy,
the net effect of gravity on the expansion of the Universe
is repulsive and so the Universe should be speeding up, rather than slowing
down! Sandage's famous deceleration parameter embodies all
of this, q0 = (
(An aside: the fact that energy density + three times
pressure is the source of gravity in Einstein's theory also leads
to the prediction of black holes. An object with very strong gravity
needs great pressure to balance gravity; objects with stronger
and stronger gravity - i.e., stars of greater and greater mass -
need more and more pressure; eventually, the pressure becomes
counterproductive, producing more gravity, resulting in a black hole.)
The prediction of accelerated expansion was confirmed
in 1998 and completed the accounting of matter and energy in the Universe.
By studying the relationship between the distances and
velocities of distant galaxies by using exploding
stars (supernovae of type Ia, or SNeIa) within them
as standard candles, two teams (the Supernova
Cosmology Project led by Saul Perlmutter and the High-redshift
Search Team led by Brian Schmidt) found
evidence that the Universe is speeding up, rather than slowing down
(Perlmutter et
al. 1998;
Riess et al. 1998).
Let me explain their results by telling you what they expected to
find and what they actually did find. Because the expansion of the
Universe is simply a scaling up of all distances, if we could measure galaxy
velocities and positions today, they would obey exactly
Hubble's law: recessional velocity proportional
to distance (v = H0 d). However,
as we look far out into space, we look back in time (light travels at
a finite speed), and so we are viewing distant galaxies at earlier
and earlier times. If the Universe is slowing down, distant galaxies
should be moving faster than Hubble's law predicts. These two
groups found the opposite: distant galaxies are moving more slowly
than Hubble's law predicts. The expansion is speeding up.
The simplest interpretation of their results is that vacuum energy,
with pressure equal to minus its energy density, contributes about
60% of the critical density, making consistent the determinations
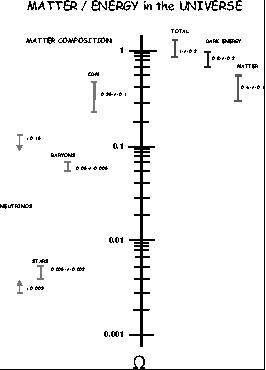
To summarize the accounting of matter and energy in the Universe
(in units of the critical density): neutrinos, 0.3% or greater;
bright stars, 0.5%; total amount of ordinary matter
(baryons), 5%; relic elementary particles, 35%; and vacuum
energy (or something similar), 60%; for a total of 100% of
the critical density (see Fig. 3).
While this accounting is not definitive yet,
measurements that are being made and will be made in the
next years could firm it up.
Figure 3. Summary of matter/energy in the
Universe. The right side refers to an overall accounting of matter
and energy; the left refers to the composition of the matter
component. The upper limit to mass density contributed
by neutrinos is based upon the failure of the hot dark
matter model of structure formation
and the lower limit follows from the
evidence for neutrino oscillations
(Fukuda et al. 1998).
Here H0 is taken to be 65 km s-1
Mpc-1.
(Only about one-tenth of the baryons are ``visible'' in the
form of bright stars. Further, because there are almost as many
neutrinos left over from the big bang as there are CMB photons and
because evidence now exists that at least two of the neutrino species have
mass, albeit very tiny
(Fukuda et al. 1998),
we can infer that neutrinos contribute as much mass,
and perhaps even more, than stars do. However, both neutrinos
and bright stars are small contributors to the total mass
in the Universe.)
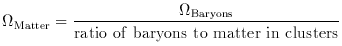
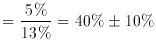
 Matter >
Matter >  Baryon. That is, the matter that provides the
cosmic infrastructure
and holds the Universe together is something exotic (or, perhaps
we should say that we are made of something more exotic). That
is a remarkable fact.
As I will discuss, the most promising idea is that this exotic
matter is relic elementary particles
left over from the earliest moments of creation.
Baryon. That is, the matter that provides the
cosmic infrastructure
and holds the Universe together is something exotic (or, perhaps
we should say that we are made of something more exotic). That
is a remarkable fact.
As I will discuss, the most promising idea is that this exotic
matter is relic elementary particles
left over from the earliest moments of creation.
 >
>  Matter. This implies
the existence of a form of matter or energy that does not clump
(as evidenced by the fact that it is not found in clusters) and
yet contributes 60% of the critical density.
The fact that this funny component to the energy density does
not clump and contributes so much of the critical density implies
that it must be very elastic (the technical term is negative pressure)
and leads to a striking prediction: that the expansion of the
Universe should be speeding up, rather than slowing down!
Matter. This implies
the existence of a form of matter or energy that does not clump
(as evidenced by the fact that it is not found in clusters) and
yet contributes 60% of the critical density.
The fact that this funny component to the energy density does
not clump and contributes so much of the critical density implies
that it must be very elastic (the technical term is negative pressure)
and leads to a striking prediction: that the expansion of the
Universe should be speeding up, rather than slowing down!
 / 2) [1 + 3p/
/ 2) [1 + 3p/ ] is negative if p < -
] is negative if p < - / 3.
/ 3.
 =1 and
=1 and  Matter = 0.4.
Vacuum energy is the modern term
we use for Einstein's cosmological constant. It corresponds to
the energy associated with the very lively quantum vacuum - pairs
of particles borrowing enough energy to exist for a fleeting instant
and then disappearing again.
Matter = 0.4.
Vacuum energy is the modern term
we use for Einstein's cosmological constant. It corresponds to
the energy associated with the very lively quantum vacuum - pairs
of particles borrowing enough energy to exist for a fleeting instant
and then disappearing again.