


Beyond the questions involving dark matter and structure formation, there is a set of more fundamental questions, ranging from the matter/antimatter asymmetry in the Universe to the origin of the expansion itself. For these questions there are attractive ideas, mainly rooted in the physics of the early Universe, which remain to be developed, suggesting that a more fundamental understanding of our Universe is possible.
Baryon/lepton asymmetry. While the laws
of physics are very nearly matter - antimatter symmetric,
the Universe is not. On scales as large as clusters of
galaxies there is no evidence for antimatter. In the context
of the hot big bang, a symmetric Universe would be even more
puzzling: at early times (t << 10-5 sec)
matter - antimatter pairs would
be as abundant as photons, but as the Universe cooled
matter and antimatter would annihilate until nucleons and
antinucleons were too rare to find one another. This would
result in only trace
amounts of matter and antimatter, a few nucleons and antinucleons
per 1018 photons, compared to the observed nucleon to
photon ratio: 
 nN / n
nN / n = (5 ± 0.5)
x 10-10.
= (5 ± 0.5)
x 10-10.
In order to avoid the annihilation catastrophe the early Universe
must possess a slight excess of matter over antimatter, i.e.,
a small net baryon number: nB / n
 nb / n
nb / n - n
- n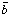 / n
/ n =
=  = 5 x 10-10. Such an
initial condition for the Universe seems as odd as having
to assume the 4He mass fraction is 25%. (Charge
neutrality requires a similar excess of electrons over positrons;
because lepton number can be hidden in the three neutrino species, it is
not possible to say that the total lepton asymmetry is comparable
to the baryon asymmetry.)
= 5 x 10-10. Such an
initial condition for the Universe seems as odd as having
to assume the 4He mass fraction is 25%. (Charge
neutrality requires a similar excess of electrons over positrons;
because lepton number can be hidden in the three neutrino species, it is
not possible to say that the total lepton asymmetry is comparable
to the baryon asymmetry.)
A framework for understanding the origin of the baryon asymmetry of the Universe was put forth in a prescient paper by Sakharov in 1967: baryon-number violating and matter - antimatter symmetry violating interactions occurring in a state of nonequilibrium allow a small, net baryon number to develop. If the idea of baryogenesis is correct, the explanation of the baryon asymmetry is not unlike that of the primeval 4He abundance (produced by nonequilibrium nuclear reactions). The key elements of baryogenesis are all in place: baryon number is violated in the standard model of particle physics (by subtle quantum mechanical effects) and in GUTs; matter - antimatter symmetry is known to be violated by a small amount in the neutral Kaon system (CP violation at the level of 10-3); and maintaining thermal equilibrium in the expanding and cooling Universe depends upon whether or not particle interactions proceed rapidly compared to the expansion rate. The details of baryogenesis have not been worked out, and may involve grand unification physics, but the basic idea is very compelling (see e.g., Kolb and Turner 1990).
The heat of the big bang. The entropy associated with the CMB and three neutrino seas is enormous: within the observable Universe, 1088 in units of kB (the number of nucleons is 10 orders of magnitude smaller). Where did all the heat come from? As we discuss in the next section, inflation may provide the answer.
Origin of the smoothness and flatness. On
large scales today and at very early times the Universe is
very smooth. (The appearance of inhomogeneity today does
belie a smooth beginning as gravity drives the growth of
fluctuations.) Since the particle horizon at last-scattering
(when matter and radiation decoupled) corresponds to an angle
of only 1° on the sky, the smoothness could not have
arisen via causal physics. (Within the isotropic and homogeneous
FLRW model no explanation is required of course.)
In a sense emphasized first by
Dicke and Peebles (1979)
and later by
Guth (1982),
the Universe is very flat. Since  0
is not drastically different from unity, the curvature radius
of the Universe is comparable to the Hubble radius. During
a matter or radiation dominated phase the curvature radius
decreases relative to the Hubble radius. This implies that
at earlier times it was even larger than the Hubble radius,
and that
0
is not drastically different from unity, the curvature radius
of the Universe is comparable to the Hubble radius. During
a matter or radiation dominated phase the curvature radius
decreases relative to the Hubble radius. This implies that
at earlier times it was even larger than the Hubble radius,
and that  was even closer to
one: |
was even closer to
one: | - 1| <
10-16 at 1 sec. To arrive at the Universe we see today,
the Universe must have begun very flat (and thus expanding
very close to the critical expansion rate).
The flatness and smoothness problems are not indicative of
any inconsistency of the standard model, but they do require
special initial conditions. Stated by
Collins & Hawking
(1973),
the set of initial conditions that evolve to a
Universe qualitatively similar to ours is of measure zero.
While not required by observational data, the inflation
model addresses both the smoothness and flatness problems.
- 1| <
10-16 at 1 sec. To arrive at the Universe we see today,
the Universe must have begun very flat (and thus expanding
very close to the critical expansion rate).
The flatness and smoothness problems are not indicative of
any inconsistency of the standard model, but they do require
special initial conditions. Stated by
Collins & Hawking
(1973),
the set of initial conditions that evolve to a
Universe qualitatively similar to ours is of measure zero.
While not required by observational data, the inflation
model addresses both the smoothness and flatness problems.
Origin of the big bang, expansion, and all that. In naming the big-bang theory Hoyle tried to call attention to the colossal big-bang event, which, in the context of general relativity corresponds to the creation of matter, space and time from a space-time singularity. In its success, the big-bang theory is a theory of the events following the big-bang singularity. In the context of general relativity the big-bang event requires no further explanation (it is consistent with ``St. Augustine's principle,'' since time is created along with space, there is no before the big bang). However, many if not most physicists believe that general relativity, which is a classical theory, is not applicable any earlier than 10-43 sec because quantum corrections should become very significant, and further, that a quantum theory of gravity will eliminate the big-bang singularity allowing the ``before the big-bang question'' to be addressed. As we will discuss, inflation addresses the big-bang question too.