


In figure 2 the true angular distance
between the
distant galaxy and the centroid of the foreground cluster is
 . As a result of the bending of the
traversing light by the
cluster, the background source appears to us to be at the
larger angular distance
. As a result of the bending of the
traversing light by the
cluster, the background source appears to us to be at the
larger angular distance  .
The lensing displacement
.
The lensing displacement
 =
=
 -
-
 is related to the gravitational
bending angle
is related to the gravitational
bending angle  by
by
where and DLS and DS are the
lens-source and
observer-source distances.6 In the thin-lens approximation, we
treat the cluster as a two-dimensional system, labeling the
projected impact parameter of a ray by the two-dimensional
vector r. Then the bending angle
Because we don't know the true, unlensed position of
the background source galaxy on the sky, we can't
measure
A source galaxy exactly behind this point mass would
appear as an "Einstein ring" image of radius
where M
How big are these effects? Single galaxies acting as
lenses of about 1012 solar masses will produce multiple
images with separations on the order of 3 arcseconds.
Cluster lenses with masses of about 1014
M
Many clusters of galaxies have measured velocity
dispersions on the order of 103 km/sec. One can calculate
the gravitational bending for fairly realistic mass distributions
7
for example a soft-core isothermal sphere, by
substituting the appropriate projected density
In 1973 William Press and James Gunn at Caltech
pointed out that a cosmologically significant density of
massive foreground objects would produce distorted and
split images of background galaxies
8 The first
gravitational lens was discovered six years later: a distant quasar
split into at least two images by the gravity of a foreground
galaxy. 9
In the 13 years since that first discovery, only eight
more unambiguous split quasar images have been found,
in searches that looked at a total of more than 4000
quasars. In several of these cosmic mirages the gravitational
lensing clearly seems to be done by an isolated
foreground galaxy dominated by its dark matter. The
rarity of these lensed quasar images is consistent with the
known abundance of quasars and foreground galaxies.
The effective mass M and radius R of the foreground
lensing galaxy can be deduced from the distortion of the
quasar image. One finds M to be on the order of 1012
M
With so few gravitationally lensed quasar images in
hand, we can't learn very much about the mass distributions
in the lenses. These background quasars typically
have redshifts on the order of 2. At these redshifts we can
see a lot more galaxies than quasars. So if we want to find
out as much as possible about dark matter in the
foreground we must avail ourselves of the great abundance
of background galaxies rather than the occasional quasar.
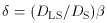
 is given in terms of
the projected two-dimensional mass density distribution
is given in terms of
the projected two-dimensional mass density distribution
 by
by
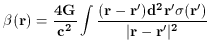
 . But its
shear - that is to say, the gradient of
the gravitational bending - is observable. For most foreground
mass distributions we can simplify the integral
equation above. If the projected density distribution
. But its
shear - that is to say, the gradient of
the gravitational bending - is observable. For most foreground
mass distributions we can simplify the integral
equation above. If the projected density distribution
 (r)
of the foreground cluster can be expressed as a sum of
circularly symmetric components, the vector arguments
reduce to scalar angles. In the simple case of a foreground
point mass,
(r)
of the foreground cluster can be expressed as a sum of
circularly symmetric components, the vector arguments
reduce to scalar angles. In the simple case of a foreground
point mass,  =
4GM / rc2, where
2GM / c2 is the
Schwarzschild radius of the mass M.
=
4GM / rc2, where
2GM / c2 is the
Schwarzschild radius of the mass M.
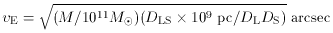
 is the
mass of the Sun. If the lensing mass is
elliptical or otherwise not circularly symmetric, this ring
symmetry is broken. Therefore complete, circular Einstein
rings are rare in the heavens. If the source angle
is the
mass of the Sun. If the lensing mass is
elliptical or otherwise not circularly symmetric, this ring
symmetry is broken. Therefore complete, circular Einstein
rings are rare in the heavens. If the source angle
 is
less than vE one sees two images of the source, separated
by about 2vE.
is
less than vE one sees two images of the source, separated
by about 2vE.
 can produce
image separations as large as an arcminute. For a
gravitationally bound collection of luminous objects, the
virial theorem lets one deduce the total mass, visible and
invisible, from the observable velocities. The theorem
states that the binding energy of the system equals its
internal kinetic energy. It follows that
<
can produce
image separations as large as an arcminute. For a
gravitationally bound collection of luminous objects, the
virial theorem lets one deduce the total mass, visible and
invisible, from the observable velocities. The theorem
states that the binding energy of the system equals its
internal kinetic energy. It follows that
< v2>, the square
of the velocity dispersion of observable components within
a distance r of the center, equals GM(r) / r. For an
equilibrated, isothermal distribution of gravitationally
bound masses, the gravitational bending angle
v2>, the square
of the velocity dispersion of observable components within
a distance r of the center, equals GM(r) / r. For an
equilibrated, isothermal distribution of gravitationally
bound masses, the gravitational bending angle
 will just
be 4
will just
be 4 <
< v2> /
c2. (Isothermality
implies that mass density
falls like r-2.) The velocity dispersion also gives the
Einstein-ring size:
v2> /
c2. (Isothermality
implies that mass density
falls like r-2.) The velocity dispersion also gives the
Einstein-ring size:
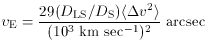
 (r) into
the integral that gives
(r) into
the integral that gives
 (r).
Generally the image
distortion or, in the case of split images, the separation between
images depends only on the mass distribution interior to
the impact parameter r.
(r).
Generally the image
distortion or, in the case of split images, the separation between
images depends only on the mass distribution interior to
the impact parameter r.
 and M/R around 3 x 1010
M
and M/R around 3 x 1010
M / kpc. This is in
accord with
typical virial theorem results for heavy galaxies.
10 Dark
matter appears to account for about 90% of M.
/ kpc. This is in
accord with
typical virial theorem results for heavy galaxies.
10 Dark
matter appears to account for about 90% of M.