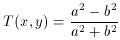It is instructive to simulate the gravitational distortions of background galaxies by tracing rays through different realistic models of foreground clusters. We then compare our real observations with what the simulations give for different cluster distributions of luminous and dark matter. For these simulations we synthesize background galaxy fields to have the same statistical distributions of shape and intensity we have seen in the deep surveys. We place these background galaxies at redshifts ranging from 0.5 to 2.0. We place the dark matter that dominates the simulated lensing cluster in various soft-core mass distributions with various velocity dispersions. After we have calculated the gravitational distortion of the background by a simulated cluster, we fold in atmospheric blurring, add Poisson noise and present the results in bins appropriate to the resolution of the CCD detectors.
Figure 4 shows the results of such a simulation
with various masses of
dark and luminous matter in the foreground cluster. The foreground
galaxies of the cluster are not shown. (In real observations they are
removed by subtracting images taken with different color filters.) In
figure 4a we see the simulated field of faint
blue background galaxies
distorted only by atmospheric blurring. The mass of the foreground
cluster has been set to zero. In figures 4b and
4c we've turned on the
foreground cluster mass. By the virial theorem, a cluster's total mass
is proportional to
<
v2> of its visible
component. So we can use the rms velocity dispersion to label mass. In
both 4b and 4c the
dark matter component of the foreground cluster is
given a core radius of 60 kpc. That's about ten times the radius of a
typical galaxy.
|
Figure 4. Computer simulations of a background field of faint blue galaxies seen through a gravitational lensing foreground cluster (not shown) whose mass, as measured by its velocity dispersion, is a variable parameter. In a the cluster mass is set at zero, so there is no gravitational lensing. In b the velocity dispersion of the cluster's galaxies is 1200 km/sec. In c a greater cluster mass produces more distortion. Here the velocity dispersion is 1800 km/sec. |
In Figure 4b the velocity dispersion of the foreground cluster is set at 1200 km/sec. The lensing mass is higher in Figure 4c, where the velocity dispersion has been raised to 1800 km/sec. The dark matter is not distributed with strict spherical symmetry; mass has been added to each individual cluster galaxy. Both these figures exhibit evident distortion of the background field. The gravitational lensing effect of the massive foreground cluster is to stretch the image of the background galaxy along a circular arc centered on the cluster. And indeed that's the kind of thing we see when we look at the field of faint blue background galaxies in parts of the sky near foreground clusters with high velocity dispersion. By comparing the Monte Carlo simulations with the CCD observations we are able to narrow down the parameter space that describes the elusive dark matter.
The systematic alignment of the ellipticities of the background images provides a strong gravitational signal. We characterize this image-stretching by a dimensionless combination of two measured length parameters in two orthogonal directions: the intensity-weighted second moments of the distorted image along the radius from the center of the lens and in the orthogonal direction on the sky. These moments are labeled b and a, respectively, in Figure 2. To detect the coherent stretching by the lens in the presence of noise and the intrinsic shape variations of galaxies, we average these scale lengths over all the background galaxies for a given putative lensing center. From the two mean scale lengths we form a dimensionless quantity, similar to an ellipticity, called the net tangential alignment or lens distortion and denoted by T. The lens distortion is related to the projected mass density clumping. It is defined 11 in terms of the moments a(x,y) and b(x,y) about any reference point (x,y) in the image plane by
An unlensed population of randomly placed and oriented galaxies will
give a net distortion T(x,y) of zero about every point
(x,y) in the image plane, while a population of lensed galaxies
will yield a positive value at the point corresponding to the actual
lens center. To construct an approximate map of the mass distribution
that did the gravitational lensing, we compute the distortion
parameter T(x,y) for a grid array of candidate lens centers. At
the effective center of a real lens, T(x,y) will exhibit a
maximum.
