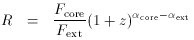
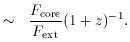
We do not correct for the fact that Fext diminishes faster with redshift than Fcore, as this depends on the source morphology. [In any case it is not a large effect. The corrections calculated by Perlman and Stocke 1993 for 14 BL Lac objects with redshifts from 0.2 to 0.5 are roughly proportional to (1 + z)1.2.]
We associate the core with the relativistically beamed jet and the extended power with the unbeamed emission. In terms of the beaming formalism,
where Lj is the observed jet luminosity [Eq. (B7)],
The largest angle between the jet and the line of sight for beamed objects is
a critical angle,
Conversely, the largest ratio, Rmax
If there is a range of Lorentz factors, Rmax is evaluated at
For large angles (
The relationship between
our parameter f and RT
For
Combining the maximum value of R for a set of beamed objects,
Rmax, b,
and the minimum value of R for the parent population,
Rmin, unb, gives
a lower limit to the value of 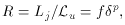
 u is the
unbeamed luminosity, f
u is the
unbeamed luminosity, f 
 j /
j /  u is the ratio of intrinsic jet to
unbeamed luminosity,
u is the ratio of intrinsic jet to
unbeamed luminosity,  is the
Doppler factor, and p is the
appropriate exponent (Appendix B). We
call sources ``beamed'' when R >
Rmin ~ 1.
is the
Doppler factor, and p is the
appropriate exponent (Appendix B). We
call sources ``beamed'' when R >
Rmin ~ 1.
 c, defined by the condition
Rmin
c, defined by the condition
Rmin
 f
f  pmin, where
pmin, where  min =
min =
 (
( c). That is,
c). That is,
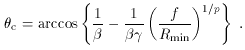
 f
f  pmax,
will occur at the smallest angle,
pmax,
will occur at the smallest angle,  min. If
min. If
 min =
0°, as is usually the case, then
min =
0°, as is usually the case, then
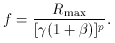
 max. If
max. If
 min
min  0°, as is the case for
SSRQ, R will be maximum for
0°, as is the case for
SSRQ, R will be maximum for  = 1 / sin
= 1 / sin  min.
min.

 arccos [0.5 /
arccos [0.5 /  ]),
emission from the
receding jet is no longer negligible and Eq. (C3) is replaced by
]),
emission from the
receding jet is no longer negligible and Eq. (C3) is replaced by
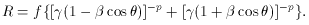
 R(90°) used
by other authors (e.g.,
Orr and Browne 1982)
is given by
R(90°) used
by other authors (e.g.,
Orr and Browne 1982)
is given by
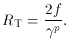
 min = 0°,
Rmax = f [
min = 0°,
Rmax = f [ (1-
(1- )]-p
)]-p  f (2
f (2 )p, so that
Rmax / RT
)p, so that
Rmax / RT  2p-1
2p-1
 2p.
This implies
2p.
This implies
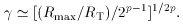
 (since Rmax /
RT
(since Rmax /
RT  Rmax, b / Rmin, unb). In the case of
a distribution of
Rmax, b / Rmin, unb). In the case of
a distribution of  s,
the Lorentz factor derived from this argument is the largest one,
since that will be responsible both for Rmax (
s,
the Lorentz factor derived from this argument is the largest one,
since that will be responsible both for Rmax (
 p) and
RT (
p) and
RT (
 -p).
-p).


