

During galaxy formation, a central condensation of mass emerged in the nuclei of most proto-galaxies, which in a majority of cases probably evolved into a supermassive black hole. A part of the remaining mass should then have had enough angular momentum to form an accretion disk in differential rotation around the black hole. Exactly how the gravitational energy is converted into radiation is unknown. The standard alternative is turbulent viscosity opposing the shear in the disk, producing heat radiation which is emitted from the disk surfaces. Another is dissipation in a hot, optically thin plasma exterior to the inner accretion disk. The resulting radiation should power several high-energy phenomena in active galactic nuclei (AGN), even though some energy may be extracted from the black hole rotation.
The combination of a disk and a supermassive black hole may thus be directly responsible for the observed continuum (Section 2), the ionization of clouds and line formation in the inner nucleus (Section 3) and possibly the formation of jets. As the matter supply to the nuclei decreased, AGN activity declined to the present-day low level.
The standard (circumstantial) arguments 1, 2 in favour of the above picture contain no conclusive evidence of either accretion disks or black holes in AGN. It could be that some of the recent developments discussed below will be able to change this situation.
In the following, some fiducial values of standard parameters will be needed. The radius of a Schwarzschild black hole is
where G is the gravitational constant, c the speed of
light and M8 the
central mass M in units of 108 M
Another fundamental parameter is the Eddington luminosity, given by
where mp is the proton mass and
where
Disks with
Figure 1. The relation between central mass
M and accretion rate 
 . The light-crossing time
corresponding to this radius is
. The light-crossing time
corresponding to this radius is

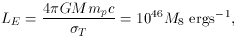
 T the Thomson cross section for
electron scattering. A spherical source with this luminosity has
enough radiation pressure to balance the inward directed gravitational
pull. One may subsequently define a critical accretion rate
T the Thomson cross section for
electron scattering. A spherical source with this luminosity has
enough radiation pressure to balance the inward directed gravitational
pull. One may subsequently define a critical accretion rate

 E is the
Eddington accretion rate and
E is the
Eddington accretion rate and  0.1 =
0.1 =  / 0.1 the scaled
accretion efficiency. This leads to the dimensionless accretion rate
/ 0.1 the scaled
accretion efficiency. This leads to the dimensionless accretion rate
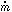

 /
/  c = L /
LE, which measures the total disk luminosity in terms of
the Eddington one.
c = L /
LE, which measures the total disk luminosity in terms of
the Eddington one.
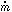 << 1, ~ 1 and >> 1
are referred to as thin, slim and
thick, respectively, which reflects the increase of vertical extent of
the disk, as
<< 1, ~ 1 and >> 1
are referred to as thin, slim and
thick, respectively, which reflects the increase of vertical extent of
the disk, as 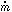 increases. The
thickening results from the
corresponding growth of internal pressure. Many AGN seem to accrete at
a rate
increases. The
thickening results from the
corresponding growth of internal pressure. Many AGN seem to accrete at
a rate 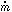 ~ 1
(Fig. 1), implying that the standard Shakura and
Sunyaev 3,
4 thin disk
model does not provide a relevant description of
the inner region, where most of the gravitational energy is
released. An increasing number of observational arguments has also
diminished the relevance of the thin disk model.
6 The
more appropriate
slim disk models have been described in detail elsewhere.
7 -
10 Such disks
are able to give a physically relevant description of the inner disk
region, including effects like transonic radial motion, pressure,
velocity and entropy gradients and non-Keplerian rotation. If
stability properties (for instance, local instabilities) of such disks
can be connected with observed variability patterns, it may be
possible to constrain several rather fundamental parameters, such as
the accretion rate and the central mass. Hence, the use especially of
X-ray variability may provide the key to an increased understanding of
the central engine, which in this context refers to radii between ~ 3
and 102 rg in the disk.
~ 1
(Fig. 1), implying that the standard Shakura and
Sunyaev 3,
4 thin disk
model does not provide a relevant description of
the inner region, where most of the gravitational energy is
released. An increasing number of observational arguments has also
diminished the relevance of the thin disk model.
6 The
more appropriate
slim disk models have been described in detail elsewhere.
7 -
10 Such disks
are able to give a physically relevant description of the inner disk
region, including effects like transonic radial motion, pressure,
velocity and entropy gradients and non-Keplerian rotation. If
stability properties (for instance, local instabilities) of such disks
can be connected with observed variability patterns, it may be
possible to constrain several rather fundamental parameters, such as
the accretion rate and the central mass. Hence, the use especially of
X-ray variability may provide the key to an increased understanding of
the central engine, which in this context refers to radii between ~ 3
and 102 rg in the disk.
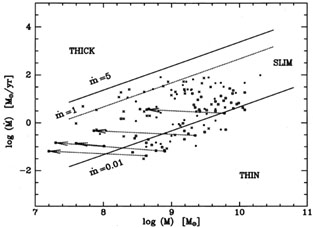
 in
typical AGN. Adapted from Ref.
5.
in
typical AGN. Adapted from Ref.
5.