


4.2 Methods of Inferring the Mass
As pointed out by Richstone, 116 one possibility to infer the presence of black holes is first to determine the central mass, and then to rule out alternatives to a black hole. This is similar to the stellar case within our Galaxy, where the central mass in some cases exceeds the maximal one allowed for a neutron star. 117 Methods of inferring the central mass in AGN include:
I. Stellar kinematics
The black hole hypothesis implies the existence of central black holes in nearly all galaxies. Interestingly, recent observations have indicated the presence of dark, massive concentrations of matter in nearby galactic nuclei. The basis of these investigations is the collisionless Boltzmann equation
where v is a typical rotation velocity, R the size scale,
F a function
of the deprojected star density
It should be stressed that even though this approach may have given
support to the first of Richstone's steps, the second one still
remains to be done. Indeed, the central mass can, for instance,
comprise a non-relativistic, compact cluster of low-mass stars,
instead of a black hole.
116
The observed stellar motion could also be
influenced by forces from outside the galactic nucleus, and the
inherent assumptions of the stellar kinematical models may be
irrelevant. Furthermore, the method seems limited to nearby, edge-on
and fast rotating spiral galaxies.
122
II. Bolometric luminosity
The basic accretion formula L =
where T is the lifetime of the AGN. If we assume (from, e.g., the
extension of extragalactic jets) T ~ 108 years, a
luminosity ~ 1046
ergs s-1 and
III. Properties of the broad-line region
The basic assumption is that the cloud motion is purely gravitational,
which, as discussed above, may be irrelevant. The first term in
Eq. (8) is used, where now v is the BLR cloud velocity and R the BLR
size. In addition, a multiplying factor
IV. Continuum properties
Accretion disk spectra have been rather successfully fitted to
UV-optical continua.
27, 36 The original models have been extended to
include general relativistic, geometrical and opacity effects. Since
the central engine is utilized, the reliability of the method may be
higher than for previous approaches.
A higher inclination angle implies a harder spectrum, whereas a
higher mass has the opposite effect (the maximum disk temperature is
inversely proportional to the mass). The result is a correlation
between the inclination angle and the mass, which reduces the number
of fitting parameters from three to two: [
The cases which show simultaneous variability in UV and optical
probably require that reprocessing must also be taken into account.
Malkan
126
adopted a simple model, in which reprocessing was assumed to
dominate outside a critical disk radius rc, whereas
the emission was due to ``normal'' viscous dissipation inside
rc. Moving the latter
inwards obviously increases the relative fraction of reprocessed
optical flux, amounting to ~ 27% for rc ~ 25
rg. Since the reprocessed
flux comes out in optical and UV, the ``original'' disk emission in
these ranges must be decreased, which is accomplished by a decrease in
the central mass. In the case of NGC 5548, consistency requires
M8 to
decrease from 2 to 0.55. This in turn implies a hotter disk, which
shifts much of the emission into the unobserved EUV region.
If problems concerning the adopted disk model (usually of the
inappropriate Shakura-Sunyaev type), the inclination angle, the
reprocessing and relative contributions from stars and the BLR can be
resolved, spectral fits using accretion disks may provide reliable
estimates of the central mass.
V. X-ray variability - NGC 6814
The short (~ 103 s) variability timescale in X-rays indicates an
origin also in the central engine (cf. Eq. (2)). The only AGN which so
far has shown clear evidence of quasi-periodic X-ray variability is
NGC 6814.
127, 128 The peaks
in the power spectrum lie in the range 10-4±1 Hz,
and the variability period (~ 104 s) has been shown to be rather
constant over timescales of years, indicating
129
|
There are essentially four classes
130 of
proposed explanations for
the variability of NGC 6814, of which the first three involve a single
spot orbiting on the accretion disk surface,
131, 132 collisions
between a star and the accretion disk
133-135 and an
orbiting screen in the outer disk.
136, 137 All of
these may suffer from being fine tuned, and the reason
why the screen should have an approximately stable structure seems
obscure. The spot and screen models may have encountered further
difficulties due to the change of folded light-curve structure between
the EXOSAT and Ginga observations. This change may be explained by
Lense-Thirring precession of the orbit of the star in the collisional
model,
133
but the indication of
The fourth alternative makes use of acoustic mode behaviour in the
innermost part of the accretion disk.
10 The
slim disk acoustic instability frequency increases generally with
Figure 6. The relation between acoustic
instability frequency 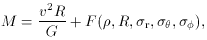
 and the three deprojected components
of the velocity dispersion
and the three deprojected components
of the velocity dispersion  r,
r, 
 and
and

 . Using various kinematic
stellar models to fit the data, the result is M8 ~ 0.1
for M31
118 and
~ 0.6 for M32,
116, 119 ~ 10 for
NGC 4594
120
and ~ 1-10 for NGC 3115.
121, 122 The
famous case of M87 seems unsettled at present.
123
. Using various kinematic
stellar models to fit the data, the result is M8 ~ 0.1
for M31
118 and
~ 0.6 for M32,
116, 119 ~ 10 for
NGC 4594
120
and ~ 1-10 for NGC 3115.
121, 122 The
famous case of M87 seems unsettled at present.
123

 c2 yields
c2 yields
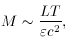
 ~
0.1, we obtain M8 ~ 0.1. In practice, only L is an
observable, so statistical arguments (involving radiation density
estimates from QSO counts) are invoked.
117, 117 The result
lies in the
range M8 ~ 0.1-10. The nature of individual central
objects may be difficult to determine using this method.
~
0.1, we obtain M8 ~ 0.1. In practice, only L is an
observable, so statistical arguments (involving radiation density
estimates from QSO counts) are invoked.
117, 117 The result
lies in the
range M8 ~ 0.1-10. The nature of individual central
objects may be difficult to determine using this method.
 ~ 1 is usually added, whose
value depends on whether the motion is bound or not. Gaskell
85 pointed
out that the direction of the motion is also needed, since a pure
outflow says very little about the central mass. Some results for
nearby Seyferts are: M8 ~ 0.1 for
NGC 5548,
105 ~ 0.5
for NGC 4151
85
and ~ 8 for F9.
104 In
order to establish the necessary infall of
matter, the method uses the cross-correlation technique between line
wing variations. The uncertain size and velocity field structure
discussed above limit the relevance of this method. Also, the nature
of the central object seems difficult to infer, since the BLR effects
occur outside the central engine.
~ 1 is usually added, whose
value depends on whether the motion is bound or not. Gaskell
85 pointed
out that the direction of the motion is also needed, since a pure
outflow says very little about the central mass. Some results for
nearby Seyferts are: M8 ~ 0.1 for
NGC 5548,
105 ~ 0.5
for NGC 4151
85
and ~ 8 for F9.
104 In
order to establish the necessary infall of
matter, the method uses the cross-correlation technique between line
wing variations. The uncertain size and velocity field structure
discussed above limit the relevance of this method. Also, the nature
of the central object seems difficult to infer, since the BLR effects
occur outside the central engine.
 , M(cos i)]. Although these
two parameters can be constrained rather tightly, the allowed range in
central mass becomes large, since the inclination angle is
undetermined. Typical results for a disk without reprocessing are
M8
~ 0.1-10 for Seyfert 1s and M8 ~ 1-100 for elliptical
galaxies. 36
, M(cos i)]. Although these
two parameters can be constrained rather tightly, the allowed range in
central mass becomes large, since the inclination angle is
undetermined. Typical results for a disk without reprocessing are
M8
~ 0.1-10 for Seyfert 1s and M8 ~ 1-100 for elliptical
galaxies. 36
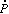 |
|
 10-6. The period
also seems virtually uncoupled to luminosity (and hence accretion
rate) variations.
10-6. The period
also seems virtually uncoupled to luminosity (and hence accretion
rate) variations.
 > 0 may have imposed major
difficulties for this scenario, since the opposite effect is
expected.
138
> 0 may have imposed major
difficulties for this scenario, since the opposite effect is
expected.
138
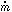 , which partially may
explain the horizontal branch oscillations (HBOs) observed in X-ray
binaries. 9
However, the instability frequency becomes essentially
constant (for a specific radius), when the accretion rate is low
(Fig. 6). Thus, the only model which at present
seems able to explain the
stability and the numerical value of the period, its long-term trend
(as indicated by
, which partially may
explain the horizontal branch oscillations (HBOs) observed in X-ray
binaries. 9
However, the instability frequency becomes essentially
constant (for a specific radius), when the accretion rate is low
(Fig. 6). Thus, the only model which at present
seems able to explain the
stability and the numerical value of the period, its long-term trend
(as indicated by 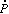 > 0) as well as
the change of topology of the folded light-curve may be the acoustic one.
139
Also, the presence of a
supermassive black hole in NGC 6814 seems strongly supported, since a
central mass M8 ~ 10-2 then would reside
within a volume only a few
Schwarzschild radii across. Independent global, numerical and
time-dependent calculations of acoustic mode behaviour
140, 141 are
consistent with this conclusion. Provided the acoustic model holds
true, the same behaviour should also apply to other sources, if the
inner accretion disk can be observed, and if the accretion rate is
low. A search for such sources should consequently concentrate on
nearby, low-luminosity and face-on AGN, or their stellar galactic
counterparts.
> 0) as well as
the change of topology of the folded light-curve may be the acoustic one.
139
Also, the presence of a
supermassive black hole in NGC 6814 seems strongly supported, since a
central mass M8 ~ 10-2 then would reside
within a volume only a few
Schwarzschild radii across. Independent global, numerical and
time-dependent calculations of acoustic mode behaviour
140, 141 are
consistent with this conclusion. Provided the acoustic model holds
true, the same behaviour should also apply to other sources, if the
inner accretion disk can be observed, and if the accretion rate is
low. A search for such sources should consequently concentrate on
nearby, low-luminosity and face-on AGN, or their stellar galactic
counterparts.
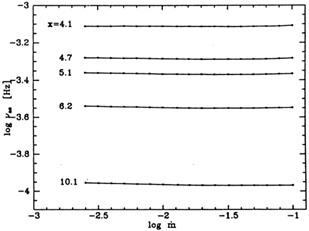
 ac and
accretion rate
ac and
accretion rate 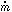 in the inner
region of a slim disk. The quantity x is
the radius in Schwarzschild units. From Ref.
139.
in the inner
region of a slim disk. The quantity x is
the radius in Schwarzschild units. From Ref.
139.