


The Cosmological Principle (CP) is the rudimentary foundation of most standard cosmological models. The CP can be summarized by two principles of spatial invariance. The first invariance is isomorphism under translation and is referred to as homogeneity. An example of homogeneity can be seen in a carton of homogeneous milk. The milk or liquid, looks the same no matter where one is located within it. In the realm of cosmology, this corresponds to galaxies being uniformly distributed throughout the universe. This uniformity would be independent of the location one chooses to make the observations. Thus, a translation from one galaxy to another would leave the galactic distribution invariant (invariance under translation).
The next element of the CP is perhaps more difficult to be realized physically. This invariance is isomorphism under rotation and is referred to as isotropy. A simple way of visualizing isotropy is to say that direction, such as North or South, can not be distinguished. For example, if one were constrained to live on the surface of a uniform sphere, there would be no geometrical method to distinguish a direction in space. Although, as soon as features are introduced on the sphere (such as land masses or cracks in the surface of the sphere), the symmetry is lost and direction can be established. This fact gives a clue that isotropy, as you might have guessed, is closely related to homogeneity.
The concepts of homogeneity and isotropy may appear contradictory to local observation. The Earth and the solar system are not homogeneous nor isotropic. Matter clumps together to form objects like galaxies, stars, and planets with voids of near-vacuum in between. However, when one views the universe on a large scale, galaxies appear `smeared out' and the CP holds.
Experimental proof of isotropy and homogeneity has been approached
using a number of methods. One of the most convincing
observations is referred to as the Cosmic Background Radiation
(CBR). In the standard Big Bang model, the universe began at a
singularity of infinite density and infinite temperature. As the
universe expanded it began to cool allowing nucleons to combine
and then atoms to form. About 300,000 years after the Big Bang,
radiation decoupled from matter, allowing it to `escape' at the
speed of light. This radiation continues to cool to the present
day and is observed as the CBR. Any observation of the CBR gives
a picture of the mass distribution at around 300,000 years. The
temperature of the CBR, first predicted theoretically in the
1960's by Alpher and Herman at 5K
[1], and Gamow at a
higher 50K [2],
was not taken seriously. A later prediction by Dicke, et. al.
[3] yielded
 3 K,
but as Dicke and colleagues set out to measure this remnant
radiation, they found someone had already made this measurement.
Dicke remarked, ``Well boys, we've been scooped''
[4].
3 K,
but as Dicke and colleagues set out to measure this remnant
radiation, they found someone had already made this measurement.
Dicke remarked, ``Well boys, we've been scooped''
[4].
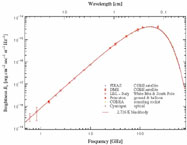
The first successful measurement of the CBR was made in 1964 by Penzias and Wilson, two scientists working on a satellite development project for Bell Labs [4]. Their measurements revealed that the CBR was characteristic of a black-body with a corresponding temperature of around 3K as illustrated in Figure (1) [4]. The measured wavelengths were on the order of 7.35 cm, corresponding to the microwave range of the electromagnetic spectrum. The CBR in this range is referred to as the Cosmic Microwave Background (CMB) (1)
|
Figure 1. The cosmic background spectrum is that of a near perfect blackbody as predicted by theory. The above graph represents the most recent observations by a number of collaborations. Graph courtesy of Wayne Hu [64]. |
Another important observation of Penzias and Wilson is the fact that the CMB is uniform (homogeneous) in all directions (isotropic). Thus, the CMB offers an experimental proof of the isotropy and homogeneity of the universe.
Because of its importance, further measurements of the CBR have been carried out. One such project named COBE, for Cosmic Background Explorer, in 1989, measured the CBR to have a temperature of 2.73 K and a distribution that is isotropic to one part in 105 [5]. COBE also has the distinction of being the first satellite dedicated solely to cosmology. Future measurements will be made by dedicated satellites like COBE, but these satellites will have much higher angular resolution. They are planned to be launched around the beginning of the century. One program directed by NASA is called MAP, for Microwave Anisotropy Probe (2) and another named the PLANCK Explorer is being launched by the European Space Agency (3) The accurate measurement of the CBR offers an observational test of cosmological models, as well as, the CP.
In addition to these benefits of CBR observations, the CBR can also be used to setup a Cosmic Rest Frame (CRF). This concept is reminiscent to the ideas of Ernst Mach. One chooses a reference frame to coincide with the Hubble expansion, i.e., with the motion of the average distribution of matter in the universe. It is convenient to define our coordinates in this frame to save confusion in measurements such as the expansion of spacetime and the Hubble Constant; however, these coordinates are in no way `absolute' coordinates. Using the CBR to define the CRF and taking galaxies as the test particles of the model serves to greatly simplify the dynamics in an expanding universe. The CRF is used to ease calculations and make the interpretation of the dynamics of an expanding universe more tractable.
The current and proposed measurements of the CBR offer a convincing test of the homogeneity of space. Measurements of the temperature of the CBR are uniform to one part in 105. This suggests the universe is homogeneous and isotropic to a high degree of accuracy. However, since this measurement is taken from our (the Earth's) vantage point, one can not assume the same conclusion from another vantage point. This can be remedied by considering how the CBR is related to the distribution of matter at the time the photons of the CBR decoupled. This offers a `snap shot' of the inhomogeneities in the density of the universe. If these regions contained more inhomogeneity, galaxies would not be visible today. This idea will be discussed in more detail later; as an alternative one can introduce the Copernican Principle (CP).
The CP states that no observers occupy a special place in the universe. This appears to be a favorable prediction, based on the evidence above, as well as lessons coming from the past. For example, the correct model of the solar system was not realized until humans realized they were not the center of the solar system. This may be a bit humbling to the human ego, but the Copernican Principle, along with homogeneity and isotropy, serve to greatly simplify the number of possible cosmological models for the universe. Later, it will be seen that homogeneity follows naturally from inflation. If the universe went through a brief period of rapid expansion, the fact that galaxies exist at all will be a necessary and sufficient condition for a homogeneous universe.
There is also the proposal for cosmic `no-hair' theorems. These theorems are similar to the `no-hair' proposal of black holes, which predict that any object that contains an event horizon will yield a Schwartzschild spherically symmetric solution at the singularity. The Big-Bang singularity is no exception, and the event horizon is the Hubble distance to be explored in sections to come. For now, experiment suggests that it is safe to assume the Copernican Principle is valid.
Below is a brief descriptive summary of observational methods for testing the CP:
The established concepts of the CP aid in simplification of cosmological models, but a further simplification can be made by invoking the Perfect Cosmological Principle. This principle differs from the previous one in that it assumes temporal homogeneity and isotropy. This would imply a static universe, for if the universe were expanding or contracting it would not look the same now, as it did in the past. However, one exception that will prove important later is the case of a (anti or quasi) DeSitter Space. By the observations of Edwin Hubble and the theoretical work by Lamaître (5) it was shown that the expansion of the universe is an accurate assumption. CP models further suggest that a static universe would be as stable as a pencil standing on its end. Thus, the Perfect Cosmological Principle does not appear to be an acceptable assumption within the standard model [7]. (6)
The last element to be discussed concerning the CP is the Weyl Postulate. This postulate formally states that, ``the world lines of galaxies designated as `test particles' form a 3-bundle of nonintersecting geodesics orthogonal to a series of spacelike hypersurfaces'' [8]. In other words, the geodesics on which galaxies travel do not intersect. This adds another symmetry to the picture of the expanding universe allowing simplification of the spacetime metric and the Einstein equations.
1 The significance in making this
distinction will
manifest itself later, but it is worth noting that other
backgrounds are measurable and offer further evidence of the CP.
Back.
2 For more info see:
http://map.gsfc.nasa.gov/. Back.
3 http://astro.estec.esa.nl/SA-general/Projects/Planck/
Back.
4 http://www.sdss.org Back.
5 Lamaître will not be
mentioned further but it is worth noting that his work and
persistence, backed by the experimental efforts of Hubble, were
instrumental in convincing Einstein that the universe was indeed
expanding. After this persuasion, Einstein was quoted as saying
this was the biggest mistake of his career
[6].
Back.
6 This
is not totally correct. In some space-times, such as anti-DeSitter
space, there exists temporal homogeneity. For a rigorous
treatment of such space-times consult
[7].
Back.