C. The Flatness Problem

The flatness problem is another example of a fine-tuning problem. The contribution to the critical density by the baryon density, based on calculations from nucleosynthesis and the observed abundance of light elements, are in good agreement with observations and give _B < 0.1. The radiation density is negligible and it is believed that non-baryonic dark matter, or quintessence/dark energy (non zero cosmological constant), will contribute the remainder of the critical density, yielding = 1. Although, an anywhere within the range of 1 causes a problem.

The Friedmann equation (28) can be used to take into account how changes with time. Noting that H = /a and = / _c, one can divide (28) by H² to obtain,

Using the relationships between the scale factor and time,

and using the definition of H yields,

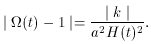
From these relations one can see that must be very fine-tuned at early times. For example, requiring to be one today, corresponds to a value of | (1) - 1 | ~ 10^-16 at the time of decoupling and a value of | (10^-43) - 1 | ~ 10^-60 at the Planck epoch. This value seems unnecessarily contrived and indicates that we live at a very special time in the universe. That is to say, when the universe happens to be flat. An alternative is that the universe has been, is, and always will be flat. However, this is a very special case and it would be nice to have a mechanism that explains why the universe is flat. The Big Bang offers no such explanation.