In several cosmological theories the observed big bang is just one
member of an
ensemble. The ensemble may consist of different expanding regions at different
times and locations in the same spacetime,
(7)
or of
different terms in the wave function of the universe.
(8)
If the vacuum energy density
V varies among
the different members of this ensemble, then the value observed by any species
of astronomers will be conditioned by the necessity that this value of
V
should be suitable for the evolution of intelligent life.
It would be a disappointment if this were the solution of the cosmological
constant problems, because we would like to be able to calculate all the
constants of nature from first principles, but it may be a disappointment that
we will have to live with. We have learned to live with similar
disappointments in the past. For instance, Kepler tried to derive the
relative distances of the
planets from the sun by a geometrical construction involving Platonic solids
nested within each other, and it was somewhat disappointing when
Newton's theory
of the solar system failed to constrain the radii of planetary orbits, but by
now we have gotten used to the fact that these radii are what they are because
of historical accidents. This is a pretty good analogy, because we do have an
anthropic explanation why the planet on which we live is in the narrow
range of distances from the sun at which the surface temperature allows
the existence of
liquid water: if the radius of our planet's orbit was not in this range, then
we would not be here. This would not be a satisfying explanation if the earth
were the only planet in the universe, for then the fact that it is just the
right distance from the sun to allow water to be liquid on its surface
would be
quite amazing. But with nine planets in our solar system and vast numbers of
planets in the rest of the universe, at different distances from their
respective stars, this sort of anthropic explanation is just common sense. In
the same way, an anthropic explanation of the value of
V makes sense if
and only if there is a very large number of big bangs, with different
values for
V.
The anthropic bound on a positive vacuum energy density is set by the
requirement that
V should
not be so large as to prevent the formation of galaxies.
(9)
Using the simple spherical infall model of Peebles
(10)
to follow the nonlinear growth of
inhomogeneities in the matter density, one finds an upper bound
where
However, we would not expect to live in a big bang in which galaxy
formation is
just barely possible. Much more reasonable is what Vilenkin calls a
principle of mediocrity,
(11)
which suggests
that we should expect to find ourselves in a big bang that is typical of those
in which intelligent life is possible. To be specific, if
Pa priori
(
We don't know how to calculate
N(
The one thing that offers some hope of actually calculating
dP
(
The fraction
N(
where
with
I should add that when anthropic considerations were first applied to the
cosmological constant, counts of galaxies as a function of
redshift
(16)
indicated that
Recently the assumptions underlying these calculations have been challenged by
Garriga and Vilenkin.
(17)
They adopt a plausible model for generating an ensemble of big bangs with
different values of
It is also assumed that in this range
V(
During the time that
so
Following this period,
The point made by Garriga and Vilenkin was that, because
V(
with V1 large, of order M4, A
and B much smaller, and M
a large
mass, but not larger than the Planck mass. This yields an a priori
probability distribution (16) that varies appreciably in the anthropically
allowed range of
It turns out (18)
that the issue of whether the a priori
probability (16) is flat in the anthropically allowed range of
where V1 is a large energy density, in the range
mW4 to
mPlanck4,
Galaxy formation is only possible for
|V(
The fractional variation in the a priori probability density (16)
as
justifying the assumptions made in the calculation of Eq. (10).
I should emphasize that no fine-tuning is needed in potentials of type
(16). It is only necessary that V1 be sufficiently
large,
where f(x) is a function of the sort we have been considering,
involving no
large or small parameters, M is a mass perhaps of order
(8
There is a problem with this sort of implementation of the anthropic
principle,
that may prevent its application to anything other than the cosmological
constant. When quantized, a scalar field with a very flat potential leads to
very light bosons, that might be expected to have been already observed. If we
want to explain the masses and charges of elementary particles
anthropically, by
supposing that these masses and charges arise from expectation values of a
scalar field in a flat potential with random initial values, then the scalar
field would have to couple to these elementary particles, and would
therefore be
created in their collisions and decays. This problem does not arise for a
scalar field that couples only to itself and gravitation (and perhaps
also to a
hidden sector of other fields that couple only to other fields in the hidden
sector and to gravitation). It is true that
such a scalar would couple to observed particles through multi-graviton
exchange, and with a cutoff at the Planck mass the Yukawa couplings of
dimensionality four that are generated in this way would in general not be
suppressed by factors of G. But in our case the
non-derivative interactions of the scalars with gravitation are suppressed by
a factor V'(
7 A. Vilenkin: Phys. Rev. D 27, 2848 (1983);
8 E. Baum: Phys.
Lett. B133, 185 (1984);
9 S. Weinberg:
Phys. Rev. Lett. 59, 2607 (1987).
Back.
10 P. J. E. Peebles:
Astrophys. J. 147, 859 (1967).
Back.
11 A. Vilenkin:
Phys. Rev. Lett. 74, 846 (1995);
12 S. Weinberg: in
Critical Dialogs
in Cosmology, ed. by N. Turok (World Scientific, Singapore, 1997).
Back.
13 H. Martel, P. Shapiro, and S. Weinberg:
Astrophys. J. 492, 29 (1998).
Back.
14 J. Gunn and J. Gott:
Astrophys. J. 176, 1 (1972).
Back.
15 G. Efstathiou:
Mon. Not. Roy. Astron. Soc. 274, L73
(1995);
16 E.
D. Loh: Phys. Rev. Lett. 57, 2865 (1986).
Back.
17 J. Garriga and A. Vilenkin:
astro-ph/9908115.
Back.
18 S. Weinberg: astro-ph/0002387.
Back.
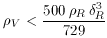
R is
the mass density and 
R
is a typical fractional
density perturbation, both taken at the time of recombination.
This is roughly the same as requiring that
V should
be no larger than the
cosmic mass density at the earliest time of galaxy formation, which for a
maximum galactic redshift of 5 would be about 200 times the present mass
density. This is a big improvement over missing by 120 orders of
magnitude, but not good enough.
V)
dV
is the a priori probability of a particular
big bang having vacuum energy density between
V and
V +
dV,
and
N(V) is
the average number of scientific civilizations in big bangs with energy density
V, then
the actual (unnormalized) probability of a scientific
civilization observing an energy density between
V and
V +
dV is
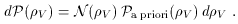
V), but it seems reasonable to
take it as proportional to the number of baryons that wind up in
galaxies, with an unknown proportionality factor that is independent of
V.
There is a complication, that the total number of baryons in a big bang may be
infinite, and may also depend on
V. In
practice, we take
N(V) as the fraction of baryons that wind up in
galaxies, which we
can hope to calculate, and include the total baryon number as a factor
in Pa priori(V).
V)
is that
N(V) is non-zero in only a narrow range of values
of V, values
that are much smaller than the energy densities typical of
elementary particle physics, so that Pa priori
(V) is
likely to be constant within this range.
(12)
The value of this constant is fixed by
the requirement that the total probability should be one, so
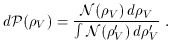
V)
of baryons in galaxies has been calculated by
Martel, Shapiro and myself,
(13)
using the well-known spherical infall model
of Gunn and Gott, (14)
in which one starts with a fractional density perturbation that is
positive within a sphere, and compensated by a negative fractional density
perturbation in a surrounding spherical shell. The results are quite
insensitive to the relative radii of the sphere and shell. Taking the shell
thickness to equal the sphere's radius, the integrated probability
distribution function for finding a vacuum energy less than or equal to
V is
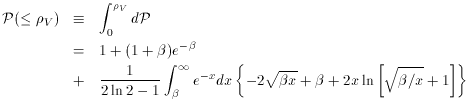
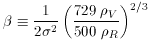
the rms fractional
density perturbation at recombination,
and R the
average mass density at recombination. The probability of
finding ourselves in a big bang with a vacuum energy density large enough to
give a present value of
V of 0.7 or less
turns out to be 5% to 12%, depending on the assumptions used to estimate
. In other words, the
vacuum energy in our big bang still seems a little low, but not implausibly so.
These anthropic considerations can therefore provide a solution to
both the
old and the new cosmological constant problems, provided of course
that the underlying assumptions are valid.
Related anthropic calculations have been carried out by several other
authors. (15)
is 0.1+0.2-0.4, and this was recognized to be too
small to be
explained anthropically. The subsequent discovery in studies of type Ia
supernova distances and redshifts that
is quite large
does not of course
prove that anthropic considerations are relevant, but it is encouraging.
V, by
supposing that there is a scalar field 
that initially can take values anywhere in a broad range in which the
potential
V() is very
flat. Specifically, in this range
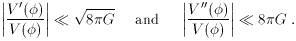
) is much less than the initial
value of the energy density
M of
matter and radiation.
For initial values of in this
range, the vacuum energy density
stays roughly constant while
M drops to
a value of order
.
To see this, note that during this period the expansion rate behaved as
H = 
/ t, with
= 2/3 or
= 1/2 during times
of matter or radiation dominance, respectively. If we tentatively assume that
is roughly
constant, then the field equation (1) gives
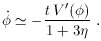
M >>
, the ratio of the kinetic to the
potential terms in Eq. (3) for
is
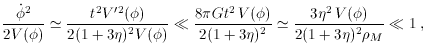
is dominated by the potential
term. The fractional change in
until the time tc when
M becomes
equal to
is then
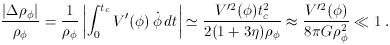
becomes dominant, and the
inequalities (12)
ensure that the expansion becomes essentially exponential, just as in theories
with the `tracker' solutions discussed in the previous section. Hence in this
class of models, V() plays
the role of a constant vacuum energy, whose
values are governed by the a priori
probability distribution for the initial values of
. In particular, if
one assumes that all initial values of
are equally probable, then the
a priori distribution of the vacuum energy is
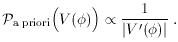
) is so
flat, the field
can vary appreciably even when
V
V() is restricted to
the very narrow anthropically allowed range of values in which galaxy
formation is possible. They concluded that it would also be possible for
the a priori
probability (16) to vary appreciably in this range, which if true would
require
modifications in the calculation of P
(
V)
described above. The potential they used as an example was
.
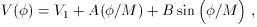
depends on
the way we impose the slow roll conditions (12). There is a large class of
potentials for which the probability is flat in this range. Suppose for
instance that, unlike the example chosen by Garriga and Vilenkin, the
potential is of the general form
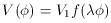
> 0 is a very small
constant, and f(x) is a function
involving no very small or very large parameters. Anthropically allowed values
of /
must be near a zero of
f(x), say a simple zero at x = a.
Then
V'()
V1 f'(a)
V1 and
V''()
^2 V1
f''(a)
2
V1, so both inequalities (12) are satisfied if
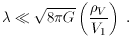
)| less than an upper bound
Vmax, of the order of the mass density of the universe at the
earliest time of galaxy formation, which is very much less than
V1, so the anthropically allowed range of values of
is
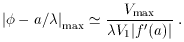
varies in the range (19) is then
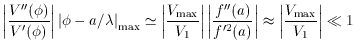
be sufficiently small, and f(x) have a simple zero somewhere, with
derivatives of order unity
at this zero. These properties are not upset if for instance we add a large
constant to the potential. But why should each appearance of the field
be accompanied with a tiny factor
? As we have been using it,
derivatives of the field appear in
the Lagrangian density in the form -
1/2 ðµ
ðµ, as shown
by the coefficient unity of the second derivative in
the field equation (1). In general, we might expect the Lagrangian density for
to take the form
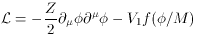
G)-1/2, and
V1 is a large constant, of order
M4. With an arbitrary
field-renormalization constant Z in the Lagrangian, the field
is not
canonically normalized, and does not obey Eq. (1). We may define a canonically
normalized field as '
Z
; writing the Lagrangian
in terms
of ', and dropping the prime, we
get a potential of the form (16), with
=
1/M Z. Thus we can
understand a very small
if we can
explain why the field renormalization constant Z is very
large. Perhaps this
has something to do with the running of Z as the length scale at
which it is measured grows to astronomical dimensions.
)
, which according to Eq. (18)
is much
less than sqrt[8 G], yielding
Yukawa couplings that are very much less than unity.
Thus it may be that anthropic considerations are relevant for the cosmological
constant, but for nothing else.
A. D. Linde: Phys. Lett. B175, 395 (1986).
Back.
S. W. Hawking: in Shelter Island II -
Proceedings of the 1983 Shelter Island Conference on Quantum Field Theory and
the Fundamental Problems of Physics,
ed. by R. Jackiw et al. (MIT Press, Cambridge, 1985);
Phys. Lett. B134, 403 (1984);
S. Coleman: Nucl. Phys. B 307, 867 (1988).
Back.
in Cosmological Constant and the Evolution
of the Universe,
ed. by K. Sato et al. (Universal Academy Press, Tokyo, 1996).
Back.
M. Tegmark and M. J. Rees:
Astrophys. J. 499, 526 (1998);
J. Garriga, M. Livio, and A. Vilenkin: astro-ph/9906210;
S. Bludman: astro-ph/0002204.
Back.