


c) The Angle Between the Ring and the Disk
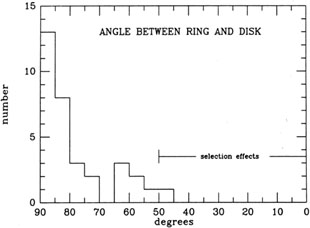
The distribution of angles between the ring and disk components may provide insight into the formation mechanism responsible for making polar-ring galaxies. For example, the statistical selection hypothesis (see Section I) would predict a relatively flat distribution, with a gradual tendency for the more oblique angles to be less prevalent since they would decay fastest due to differential precession. The observed distribution is shown in Figure 3. We find a strong tendency for the components to be nearly orthogonal (i.e., 0 degrees in Fig. 3). The distribution for the intermediate angle between 10 and 35 degrees is essentially flat. No conclusions can be drawn beyond 35 degrees since the selection effect of including only objects which are more nearly orthogonal than parallel begins to remove these objects from the sample.
|
Figure 3. The distribution of galaxies from category A and B of the PRC as a function of the angle between the ring and the perpendicular to the disk. |
These results appear to support the preferred orientation model (see Section I and Steiman-Cameron 1990) since it predicts that the systems should evolve toward the orthogonal orientation. It also suggests the possibility of two separate distributions, with the more nearly orthogonal systems being intrinsically different than the systems with intermediate orientations (e.g., perhaps they are older, and have therefore had more time to settle to the preferred plane). There is a weak correlation of the angle between the ring and disk with the asymmetry of the rings which supports this idea. The more nearly perpendicular rings are more symmetric than the oblique rings. The correlation coefficient is 0.33 with 27 galaxies in the sample. The probability of coming from a random distribution is 8%.
A possible psychological effect to consider would be that in cases that are difficult to measure because one component is relatively face on, the eye may tend to measure a more perpendicular angle. This does not appear to be a problem, however, since the distribution of angles for poor quality determinations (i.e., quality rating of 3 in Table 1) is the same as the total distribution.