


The theory of the weak interaction, which uses the intermediate W and Z bosons, is an example of the well-established new physics.
The intermediate-particle theory said that a seemingly one-step
process, such as, for example, the neutron decay n = p +
e- +  , in
fact occur via two pathways, each consisting of two steps:
, in
fact occur via two pathways, each consisting of two steps:
The intermediate states violate energy conservation in both of the
pathways; these intermediate states are called "virtual states" and are
energy barriers to the reactions. The low probability ("weakness") of
beta decay is due to the height of the barrier, i.e., the large mass of the
W-boson. The theory was triumphantly confirmed in 1983 when the W
and Z bosons were discovered - they turned out to have precisely the
masses predicted (approximately one hundred times heavier than the
proton or neutron). The Z0 boson is especially
interesting for
astronomers, because it is produced in the so-called neutral-current
reactions, which involve the scattering of neutrinos on nucleons or
electrons; for example,
where the primes are used to indicate a change in momentum and
energy (the second pathway has been omitted). These processes are
important in the dynamics of supernova explosions, since they
determine the energies of the neutrinos and the rate at which they escape
during the collapse of a stellar core. Quantum chromodynamics, which
says that all hadrons (protons, neutrons, etc.) consist of quarks and that
the interaction between quarks is produced by a gluonic field, is now at
the same level. In both cases (the W and Z particles and
the gluons), the fields are similar to the electromagnetic field.
Readers aware of the recent progress in particle physics may skip the
following elementary comments on what is meant by a vector field. Of
course, these fields have one basic property in common: they are vector
fields. This means that they may be obtained from the corresponding
vector potentials. In four-dimensional Minkowski space-time, a vector
(and, in particular, a vector potential) has four components: three
spatial components, which form a three-vector (A1,
A2, A3), and one
component directed along the time axis, which is a scalar
A4 =
The fields that act on charges are functions of the derivatives of the
potentials. For example, the electric field is
i.e., two equal charges repel one another via a vector field.
A wide variety of vector fields with different properties are used in
modern physics:
(1) The electromagnetic field is neutral and massless, which means
that free photons can have infinitely small energy and frequency.
Astronomers use this property of the electromagnetic field to explore
very distant objects, especially using long, low-frequency
electromagnetic (radio) waves. Any set of photons is neutral, which means
that it is not itself the source of a static electric field.
(2) The vector fields corresponding to the W and Z
particles are
massive. This means that the corresponding interaction has a short
range. One needs a very high energy to create the W and Z
particles.
By the same token, this means that they are unstable; they decay into
various particle pairs: W+ = p +
(3) The gluon vector is also peculiar. Gluons are massless, but have
charge. Every gluon is not only a result of the motion of charges
(quarks) and an agent acting on the quarks but also is itself a charge, i.e.,
a source for other gluon fields. The resulting (rather complicated)
situation leads to so-called quark confinement. The result is that free
gluons and quarks cannot exist. The only stable particles are
combinations of quarks and antiquarks and combinations of three quarks
(like the proton and neutron), or combinations of several gluons - but
always without free gluonic charge.
We see that the phenomena produced by the various thoroughly
studied vector fields are very different. But they all have one property
in common: a vector field defines a preferred direction at every point in
space. The preferred direction may be along a spatial axis if the spatial
component is much larger than the time-component and there exists a
reference frame in which the time-component is equal to zero. If this is
not the case, it is possible to find a coordinate system (an observer) in
which the three-vector is zero at a given point, and the four-vector is
oriented along the time axis.
2 An excellent discussion of modern
particle and field physics
is contained in Okun's book
(Okun, 1985).
Back.
3 There is a complication, especially for
the electromagnetic field. All that we said above
is true: (A, A1, A2,
A3) is a
vector, the so-called E and H fields together form a
second-rank tensor in the four-dimensional space-time complex. But the
special property
of the electromagnetic case is that one can add a gradient to A
without changing the
physical picture: the measurable E and H do not change
when this gradient is added. But
the value and even the direction of A is changed. A space-like
and a time-like A can
describe the same physical situation. This is a special property of the
electromagnetic field
due to the zero rest mass of the photon. This property is not shared by
the vector fields
describing the massive W+ and Z0
particles. Back.
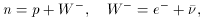
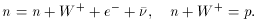
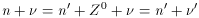
 as
long as one restricts oneself to rotations about the spatial axes. The
Lorentz transformation to a moving system is what relates the
three-scalar and the three-vector to one another. A well-known example of
a four-vector is the energy and momentum of a particle. Calling it a
four-vector means that we are prescribing its behavior in different
coordinate frames. The most important example of this is the famous
formula E = mc2 /
sqrt[1 -
as
long as one restricts oneself to rotations about the spatial axes. The
Lorentz transformation to a moving system is what relates the
three-scalar and the three-vector to one another. A well-known example of
a four-vector is the energy and momentum of a particle. Calling it a
four-vector means that we are prescribing its behavior in different
coordinate frames. The most important example of this is the famous
formula E = mc2 /
sqrt[1 -
 2], p =
mv / sqrt[1 -
2], p =
mv / sqrt[1 -
 2],
where
2],
where  = v/c. A
vector field is a space-time distribution of four-vectors: every point in
space and every instant of time has a particular vector associated with
it. (3) This means
that four functions of space and time are given:
= v/c. A
vector field is a space-time distribution of four-vectors: every point in
space and every instant of time has a particular vector associated with
it. (3) This means
that four functions of space and time are given:
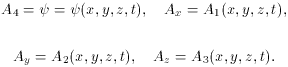
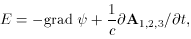
 , Z0 =
µ+ + µ- etc. Their
lifetime is on the order of 10-23 s (to be precise, only the
decay products
of the W and Z particles, not the tracks of the particles
themselves, are
experimentally observed).
, Z0 =
µ+ + µ- etc. Their
lifetime is on the order of 10-23 s (to be precise, only the
decay products
of the W and Z particles, not the tracks of the particles
themselves, are
experimentally observed).