3.5 Small-scale Velocity Field

Redshift surveys can provide statistical estimates of deviations of the Hubble flow on small scales, without requiring direct distance measurements of individual galaxies. As discussed by Davis & Peebles (1983) this can be done by examining the correlation function , as a function of the projected separation r_p and redshift separation of pairs. Deviations of (r_p, ) from concentric circles are due to redshift distortions, which provide information on the distribution function of relative peculiar velocities of galaxy pairs. On large scales, linear theory relates the first moment of this distribution to the density parameter and the linear bias parameter b. On small scales, the cosmic virial theorem connects the second moment to these parameters.

Analysis of redshift distortions observed the 1.2 Jy IRAS Survey lead to estimates of / b ~ 0.4, from the cosmic virial theorem, and = ^0.6 / b = 0.45 on scales ~ 10 h^-1 Mpc (Fisher et al. 1994). Assuming that the relative bias between optical and IRAS galaxies is b_o / b_I ~ 1.5 this result implies that ₈ ^0.6 ~ 0.3, where ₈ is the rms mass fluctuation within a sphere 8 h^-1 Mpc in radius. Unfortunately, both estimates suffer from either large systematic errors or large cosmic variance, due to the limited number of independent structures sampled by the nearby surveys. This has been vividly illustrated by the large sample-to-sample variations of the relative velocity dispersion between pairs derived from the combined CfA2-SSRS2 sample (Marzke et al. 1995). The finding that this quantity shows strong sample-to-sample variations indicates that it is poorly determined within the volume surveyed, being dominated by the shot-noise contribution of clusters. One is forced to conclude that at the present time the small-scale velocity field is not a powerful discriminant among competing cosmological models. Even though new statistics have recently been proposed to overcome the effects of a pair-weighted statistic (Davis et al. 1997, Strauss et al. 1998), it is clear that for robust measurements considerably larger volumes, sampling a fair number of clusters of different richness, are required. This will certainly be possible with the next generation of surveys. It is worth pointing out that the estimates of on small scales are consistent with the most recent estimates of this parameter from cosmic flows (e.g., da Costa et al. 1998).

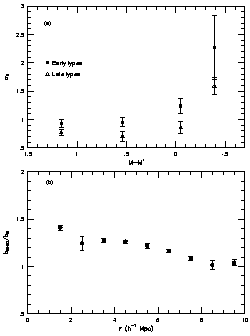
Figure 4. Linear biasing measures for early/late-type galaxies. Panel (a) shows the variance for different luminosity thresholds while panel (b) shows the relative bias between early and late types as a function of scale (for details see Willmer et al. 1998).