1.
where f = f(x, v, t) is the distribution function
normalized
so that f dx dv is the number of stars in the
phase-space volume dx dv centered on the
point (x, v). The potential,  , includes the self-consistent
field generated by the stars as well as the gravitational influence of
dark matter and gas. While the nature of the dark matter remains
enigmatic, observational constraints suggest that it too obeys
Equation 1.
, includes the self-consistent
field generated by the stars as well as the gravitational influence of
dark matter and gas. While the nature of the dark matter remains
enigmatic, observational constraints suggest that it too obeys
Equation 1.
N-Body Methods
In the purely stellar-dynamical limit, the interaction of galaxies is
a well-posed problem, in the sense that the evolution is determined
entirely by the Boltzmann equation. Unfortunately, we don't know how
to obtain relevant analytic solutions to this equation, except in the
limit of weak interactions (e.g.
Weinberg 1986,
1989) or for rather
special systems (e.g.
Sridhar & Nityananda 1990), so
numerical
methods must be used. Rather than solve the Boltzmann equation with a
finite-difference technique in six-dimensions, a Monte-Carlo
approach is employed. The initial f(x,v) is used as a
probability distribution function to pick phase-space coordinates
xi and vi for
particles i = 1, . . . , N; these particles
are then integrated along the characteristic curves of Equation 1:
dxi /
dt = vi , 2.
dvi /
dt = -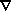
 i .
3.
i .
3.
Despite the enormous simplification entailed by Equations 2 and 3,
the evolution of interacting galaxies is quite costly to compute,
owing mainly to the difficulty of calculating the self-consistent
potential. In practice, the mass in real galaxies is much more finely
divided than in any computer model, so the model's self-consistent
potential is much noisier than that of actual galaxies. This gives
rise to an unwanted diffusion in phase-space which can alter the
structure of simulated galaxies on uncomfortably short time-scales.
Broadly speaking, the various known algorithms for computing the
potential of a system of N particles can be categorized as either
``action-at-a-distance'' or ``field'' methods. The former
explicitly treat interactions between individual particles while the
latter do so only indirectly through the contributions of particles to
the global gravitational field. The simplest action-at-a-distance
technique is direct summation. A common expression for the
gravitational potential at the location of particle i is
 (ri)
= - G
(ri)
= - G  j
j 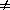 i (mj /
[ | ri - rj |2
+
i (mj /
[ | ri - rj |2
+  2]1/2) , 4.
2]1/2) , 4.
where  is the
``softening parameter.'' Direct summation is
flexible but has an asymptotic cpu cost per step scaling as ~
O (N2), limiting its practical use to small-N
systems. Nevertheless, some early investigations of the dynamics of mergers
were performed using this algorithm (e.g.
White 1978,
1979,
1980;
Gerhard 1981;
Quinn 1982) and much larger
simulations with N >
10,000 may ultimately be feasible on special-purpose machines (e.g.
Sugimoto et al. 1990).
is the
``softening parameter.'' Direct summation is
flexible but has an asymptotic cpu cost per step scaling as ~
O (N2), limiting its practical use to small-N
systems. Nevertheless, some early investigations of the dynamics of mergers
were performed using this algorithm (e.g.
White 1978,
1979,
1980;
Gerhard 1981;
Quinn 1982) and much larger
simulations with N >
10,000 may ultimately be feasible on special-purpose machines (e.g.
Sugimoto et al. 1990).
A variety of methods have been proposed to reduce the cost of
computing the self-consistent potential. For some problems, it is
expedient to neglect self-gravity altogether and evolve the system in
a potential which is known a priori, such as in test-particle
methods (e.g.
Schwarzschild 1979;
Quinn 1984), the
restricted three-body method (e.g.
Pfleiderer & Siedentopf 1961;
Toomre & Toomre 1972), or
semi-restricted N-body codes
(e.g. Lin & Tremaine 1983;
Quinn & Goodman 1986;
Hernquist & Weinberg
1989). Generally speaking, however, the dynamics of
interacting galaxies will not be represented faithfully without
including self-gravity (Barnes 1988).
The majority of the known self-consistent methods have historically
not been useful for studying systems with small filling factors in
three-dimensions such as interacting and merging galaxies. (We refer
the reader to the excellent monographs by
Sellwood [1987] and
Hockney & Eastwood [1988] for a
discussion of the limitations of grid
methods.) An exception is the technique known as the ``hierarchical
tree'' method (Appel 1985;
Jernigan 1985;
Barnes & Hut 1986) which
recently has had a significant impact on the study of colliding
galaxies. All variants of this technique are effectively gridless and
retain the essential ingredients of the action-at-a-distance
formulation. Particles are processed similarly to direct summation,
but the potential from distant groups of particles is approximated
using low-order multipole expansions. If the required manipulations
are performed using tree-structured data the cpu cost per step scales
as ~ O (N log N). In fact, it is possible to reduce the cost
even further to ~ O (N) by using tree-structured data in the
context of a field representation of the potential
(Greengard & Rokhlin 1987;
Greengard 1988). A distinct
approach, used in
``expansion codes,'' relies on the use of basis function expansions to
compute the potential from the known density field sampled by the
particles (Aarseth 1967;
Clutton-Brock 1972a,
b;
van Albada & van Gorkom 1977;
Villumsen 1982,
1983;
White 1983a;
McGlynn 1984;
Bontekoe & van Albada 1987).
As emphasized by Sellwood
(1987), the choice of method is largely
dictated by considerations of efficiency. Contrary to claims which
persist in the literature, action-at-a-distance and field methods
suffer from comparable degrees of relaxation for the same spatial
resolution and particle number
(Hernquist & Barnes 1990;
Hernquist & Ostriker 1992).
Therefore, there is no objection in principle to
using direct methods to evolve collisionless systems, provided that a
sufficiently large N can be used to suppress relaxation effects to
the extent required.
Gas-Dynamic Methods
While present-day galaxies typically contain less than 10% of
their luminous mass in this form, gas is critical to our understanding
of galactic phenomena such as starbursts and active galactic nuclei,
because it can dissipate and form stars. Galactic gas obeys the
ordinary conservation laws for a compressible fluid (e.g.
Landau & Lifshitz 1959).
However, given our present level of understanding
of the interstellar medium of even our own galaxy, the dynamics of
galactic gas is ill-posed. Because of cooling and feedback from
supernovae, interstellar gas is highly inhomogeneous and comprises
several distinct phases
(McKee & Ostriker 1977). We lack the
computational hardware and theoretical knowledge to model the different
phases simultaneously, and some compromises must necessarily be made.
One strategy, used to advantage by some workers, is to focus on global
issues where the detailed small-scale structure of the gas is
probably not crucial. In the limit where the gas can be represented
as a continuous medium, its equations of motion can be solved either
by finite-difference algorithms or by particle-based techniques. A
promising example of the latter is the method known as
smoothed-particle hydrodynamics (SPH; e.g.
Lucy 1977;
Gingold & Monaghan 1977;
Monaghan 1992). Since SPH is
Lagrangian, it does not
suffer from grid-based limitations on spatial resolution or global
geometry and is especially well-suited for studying interacting
systems. In addition, SPH can be generalized so that it is adaptive
in both space and time
(Hernquist & Katz 1989); these
refinements
offer significant advantages when dealing with large density contrasts
(Hernquist 1989a;
Barnes & Hernquist 1991).
A phenomenological treatment is sometimes useful in the opposite
extreme when the gas is modeled as a set of discrete clouds (e.g.
Negroponte & White 1983).
In the ``sticky-particle'' method,
particles representing the gas evolve similarly to collisionless
particles but undergo inelastic collisions amongst themselves, thereby
dissipating kinetic energy. Computationally, this approach is simpler
than those which solve the equations of motion for continuum gas, but
requires a number of ad hoc parameters whose
relationship to actual physical processes is problematic. Given our
ignorance of the true state of interstellar gas it is difficult to
argue for or against one of the two extremes embodied by, e.g. the SPH
or sticky-particle formalisms.



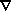
 ·
ðf / ðv = 0,
·
ðf / ðv = 0,
 , includes the self-consistent
field generated by the stars as well as the gravitational influence of
dark matter and gas. While the nature of the dark matter remains
enigmatic, observational constraints suggest that it too obeys
Equation 1.
, includes the self-consistent
field generated by the stars as well as the gravitational influence of
dark matter and gas. While the nature of the dark matter remains
enigmatic, observational constraints suggest that it too obeys
Equation 1.
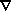
 i .
i .
 (ri)
= - G
(ri)
= - G  j
j 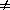 i (mj /
[ | ri - rj |2
+
i (mj /
[ | ri - rj |2
+  2]1/2) ,
2]1/2) ,  is the
``softening parameter.'' Direct summation is
flexible but has an asymptotic cpu cost per step scaling as ~
O (N2), limiting its practical use to small-N
systems. Nevertheless, some early investigations of the dynamics of mergers
were performed using this algorithm (e.g.
White 1978,
1979,
1980;
Gerhard 1981;
Quinn 1982) and much larger
simulations with N >
10,000 may ultimately be feasible on special-purpose machines (e.g.
Sugimoto et al. 1990).
is the
``softening parameter.'' Direct summation is
flexible but has an asymptotic cpu cost per step scaling as ~
O (N2), limiting its practical use to small-N
systems. Nevertheless, some early investigations of the dynamics of mergers
were performed using this algorithm (e.g.
White 1978,
1979,
1980;
Gerhard 1981;
Quinn 1982) and much larger
simulations with N >
10,000 may ultimately be feasible on special-purpose machines (e.g.
Sugimoto et al. 1990).