Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
51-74 Copyright © 1992 by Annual Reviews. All rights reserved |
In the simplest approximation HI clouds move as test particles in a
fixed, axisymmetric galactic potential  (R, z). Since they have random
velocities
(R, z). Since they have random
velocities  10 km
s-1
(van der Kruit &
Shostak 1982),
they may be assumed
to move on nearly circular orbits and their motion may be followed in the
epicycle approximation. If a cloud's orbit is inclined to its galaxy's
equatorial plane, its height z above this plane then oscillates
harmonically at angular frequency
10 km
s-1
(van der Kruit &
Shostak 1982),
they may be assumed
to move on nearly circular orbits and their motion may be followed in the
epicycle approximation. If a cloud's orbit is inclined to its galaxy's
equatorial plane, its height z above this plane then oscillates
harmonically at angular frequency  =
sqrt[ð2
=
sqrt[ð2 /
ðz2]. Meanwhile
its azimuthal coordinate
/
ðz2]. Meanwhile
its azimuthal coordinate  circulates with angular frequency
circulates with angular frequency  = R-1/2
(ð
= R-1/2
(ð / ðR)1/2. Since for an oblate potential
/ ðR)1/2. Since for an oblate potential
 >
>  , the angle at which the cloud crosses the equatorial plane
regresses with angular frequency
, the angle at which the cloud crosses the equatorial plane
regresses with angular frequency  r =
r =  -
-  .
.
Suppose a warp extends from R1 to R2 and initially has a straight line of nodes. Then the line of nodes will wrap into a leading spiral which wraps half way round the galaxy in a time
How big is
it is easy to show that
where
For a flat rotation curve,
Here sqrt[4
(a) The halo may be flattened to axis ratio q < 1. Then the
mass M (R) within cylindrical radius R required to
generate
while the circular speed vh of a spherical halo satisfies
Equating to zero the derivative w.r.t. R of
vc2 = vh2 +
vd2
and then making the approximation vd2 =
GMdisk / R yields
One frequently identifies vc with
vd's peak value
so that vd2 (R)
This gives, for example,
In real life
Typically R25
The assumption that the halo's ellipticity q
is radius independent.
Petrou (1980)
pointed out that
Neglect of non-gravitational forces. Perhaps gaseous
disks warp in response to pressures applied by an intergalactic medium. The
necessary pressure may be hydrodynamical in origin
(Kahn & Woltjer, 1959),
or due to a magnetic field
(Battaner et al., 1990,
1991).
With simple
hydrodynamical pressure it is difficult to generate an integral-sign warp;
the dominant response to the IGM's ram pressure of a disk moving through
the IGM will be axisymmetric, taking the form of a rim rather
than a warp. The anisotropy of magnetic pressure in relatively stationary,
magnetized IGM can in principle generate an integral-sign warp, but the
magnitude of the field required to distort a disk near R25 is
implausibly large: a simple calculation leads to the estimate
(Binney 1991)
where
The halo has been assumed to be axisymmetric, whereas it
is probably triaxial. Is the warp's line of nodes somehow aligned with the
halo's principal axes? This might arise because the orbits of clouds are
forced in a systematic way by the triaxiality of the halo's potential.
The disk's potential has been assumed to be fixed.
Actually the warp modifies the potential, and one must take this into
account by modelling the disk as a self-gravitating collisionless system.
This is most conveniently done by asking what running bending waves the disk
supports. Alternatively (but not equivalently) one can look for normal
modes of oscillation.
The halo potential has been assumed to be an inanimate,
unresponsive thing. The orbits of the halo's constituent particles must
respond to the variations in the disk's gravitational potential to which the
warp gives rise. This greatly complicates the already difficult mathematical
problem posed by study of bending waves and normal modes in self-gravitating
disks.
Galaxies have been assumed to be closed, isolated
things. In
reality they inhabit groups and clusters and sometimes experience close
encounters with companions. Moreover, unless we live in an open Universe,
cosmic infall onto galaxies must be an important process. Could warps arise
from the response of galaxies to changing external circumstances?
Suggestions (3)-(6) are closely connected and raise problems of formidable
difficulty which are far from being adequately understood. Many of them
require an understanding of the dynamical excitations of self-gravitating
disks.
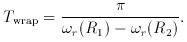
 r?
Writing Poisson's equation for an axisymmetric system in the form
r?
Writing Poisson's equation for an axisymmetric system in the form
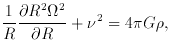
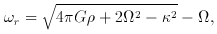
 2 =
R-3 (ðR4
2 =
R-3 (ðR4  2 / ðR) is
the square of the
radial
epicycle frequency. Equation 3 shows that
2 / ðR) is
the square of the
radial
epicycle frequency. Equation 3 shows that  r is intimately
connected with the density
r is intimately
connected with the density  far out where warps are observed; warps
are a potentially powerful probe of dark halos.
far out where warps are observed; warps
are a potentially powerful probe of dark halos.

 1 / R, we have
1 / R, we have  2 = 2
2 = 2  2 and thus that
2 and thus that
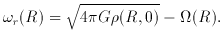
 G
G (R)]
is the value the circular frequency
(R)]
is the value the circular frequency  would
take if the galaxy were perfectly spherical and the density at general
spherical radius r were (R / r)2
would
take if the galaxy were perfectly spherical and the density at general
spherical radius r were (R / r)2 (R,
0). We expect this to differ from
the actual circular frequency
(R,
0). We expect this to differ from
the actual circular frequency  (R) for two reasons:
(R) for two reasons:
 (R)
is independent of q, while
(R)
is independent of q, while  (R, 0) is inversely proportional to q.
Thus we have
(R, 0) is inversely proportional to q.
Thus we have  r
(R) =
r
(R) =  (R)(1 /
(R)(1 /
 q - 1).
q - 1).
(b) At the radii of interest, an exponential disk contributes
significantly to  2
(R) but negligibly to
2
(R) but negligibly to  (R, 0). In fact, for
R > 4 Rd, where Rd is the
disk's scale length, the circular speed vd
of an exponential disk approximately satisfies [e.g., equation (2P-5) of
Binney & Tremaine
(1987)]
(R, 0). In fact, for
R > 4 Rd, where Rd is the
disk's scale length, the circular speed vd
of an exponential disk approximately satisfies [e.g., equation (2P-5) of
Binney & Tremaine
(1987)]
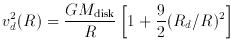
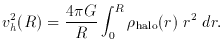
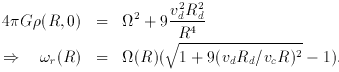
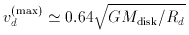
 (vc2 / 0.642)
(Rd / R). Making this identification one has
(vc2 / 0.642)
(Rd / R). Making this identification one has
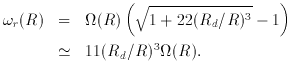
 r (4Rd)
r (4Rd)  0.16
0.16  and
and
 r
(6Rd) = 0.05
r
(6Rd) = 0.05  .
.
 r will
receive contributions from both halo
flattening and the presence of an embedded disk. Given the strong dependence
on R of the second contribution, halo flattening will dominate
at R
r will
receive contributions from both halo
flattening and the presence of an embedded disk. Given the strong dependence
on R of the second contribution, halo flattening will dominate
at R  4Rd unless the halo is remarkably spherical.
4Rd unless the halo is remarkably spherical.
 4Rd. So in the
region R25
4Rd. So in the
region R25  R
R  RH0
in which Briggs finds the line of nodes straight, we have
twrap
RH0
in which Briggs finds the line of nodes straight, we have
twrap 
 /
/
 r
(4Rd)
r
(4Rd)  6
6 /
/ 
 2Gyr even in a
spherical halo. How do lines of nodes avoid winding up on this or a shorter
time-scale? Evidently some simplifying assumption has invalidated the
calculation. Some possible culprits are:
2Gyr even in a
spherical halo. How do lines of nodes avoid winding up on this or a shorter
time-scale? Evidently some simplifying assumption has invalidated the
calculation. Some possible culprits are:
 r would not decline
outwards, and the warp would not wind up, if q were to decrease outwards
in the right way. Unfortunately, there seems to be no reason why in every
warped galaxy q should vary with radius in the approved fashion.
r would not decline
outwards, and the warp would not wind up, if q were to decrease outwards
in the right way. Unfortunately, there seems to be no reason why in every
warped galaxy q should vary with radius in the approved fashion.
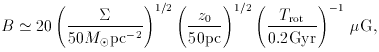
 is the warped disk's
surface density, z0 the vertical
scale of the warp, and Trot is the rotation period at
the radius of the warp. Given that a field of 2.8 µG has the
same energy density as the cosmic microwave background, it is clear that
magnetic forces will be unimportant except possibly at R
is the warped disk's
surface density, z0 the vertical
scale of the warp, and Trot is the rotation period at
the radius of the warp. Given that a field of 2.8 µG has the
same energy density as the cosmic microwave background, it is clear that
magnetic forces will be unimportant except possibly at R  40
kpc, where
40
kpc, where  is extremely
small.
is extremely
small.