Annu. Rev. Astron. Astrophys. 1992. 30: 51-74 Copyright © 1992 by Annual Reviews. All rights reserved

7. WARPS AND INFALL

The discussion so far has assumed that each galaxy is an island universe. Actually galaxies must be subject to a variety of disturbances, and warps, which usually lie outside the optically conspicuous parts of galaxies, may be connected with these disturbances.

In recent years it has become conventional to assume that the cosmic density parameter 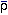/ _crit is unity, baryons contributing about 10% of the whole and non-baryonic dark matter the rest. Visible galaxies account for only ~ 1% of _crit, so conventional wisdom is that 99% of the mass of the Universe, including nine tenths of all baryons, is out there swilling around between the galaxies we know not how.

According to the standard luminosity function of galaxies, most luminosity is in galaxies with luminosities L L = 10¹⁰ h^-2 L (V) - that is, in galaxies similar to the Milky Way (L_V 1.4 h² L). There is no reason to suppose that the majority of L galaxies have finished growing. Indeed, most L galaxies are still falling towards their nearest comparable neighbours - in our case M31 - and should be foci of the cosmic flow pattern near them. Inside the optical radius of an L galaxy, the disposition of material is generally symmetrical and orderly because the dynamical time there is much shorter than the Hubble time. Further out the picture is more confused and time-dependent, for here the virialized portion of the galaxy is steadily growing as fresh shells detach themselves from the Hubble flow and fall back into the galaxy (e.g. Gunn 1977). It is useful to identify three characteristic radii:

1. r_max(t₀), the radius of the shell surrounding an L galaxy that has just ceased expanding and is on the point of falling back onto the galaxy;

2. r_max(t₀ / 3) = r_max(t₀) / 3^2/3, which is approximately the current radius of the shell which detached itself from the Hubble flow at 1/3 t₀, fell in and has now reexpanded to something approaching its maximum radius;

3. r_equi, which is the radius inside which the halo of an L galaxy can be considered to be in virial equilibrium.

The dynamics of the Local Group give a lower bound on r_max(t₀), namely r_max(t₀) 1 Mpc (e.g., Binney, 1991). An independent estimate from standard CDM theory is r_max(t₀) 2.2 Mpc (Binney, 1991), from which follows r_max(t₀ / 3) 1.1 Mpc. Thus either M31 is just past its second apocenter, or the overdensity associated with the Galaxy was initially somewhat less pronounced than average in standard CDM theory. It is probably safest to assume that M31 is close to its first rather than its second apocenter, and to divide all radii obtained from CDM theory by 2.

Clearly the galactic halo cannot be considered to be in any kind of dynamical equilibrium at radii comparable to r_max(t₀ / 3). Indeed the zone within which cosmic infall generates significant fluctuations in the gravitational potential will extend in to at least the radius r_1peri typical of the pericenters of material that has just reached its first pericenter, and more conservatively in to r_2peri, the typical pericentric distance of material now at its second pericenter.

The radii r_1peri and r_2peri depend on how much angular momentum with respect to the Galactic center infalling lumps pick up. Binney (1991) estimates the RMS angular momenta of shells from CDM theory and concludes that r_1peri 200 kpc, r_1peri 60 kpc. These results suggest that a reasonable estimate of the region within which freshly added material is settling down to dynamical equilibrium is 70 kpc < r < 300 kpc, while infall reigns from 300 kpc out to 1 Mpc or so. Perhaps r_equi 70 kpc is the best estimate of the outer boundary of the virialized portion of the Galaxy.

Ryden & Gunn (1987) and Ryden (1988) have shown in the context of CDM theory (a) that half any Galaxy's total angular momentum was contributed by material that fell in over the last third of a Hubble time, and (b) that the direction of the angular momentum vector of the currently infalling shell reorientates itself roughly with every doubling of the Hubble time. Quinn & Binney (1991) have refined this calculation and argue that the angular momenta of shells differing in unperturbed radius by more than a factor ~ 2 are anti-correlated. This anti-correlation implies that on the average galaxies reverse the directions of their net spin vectors with every doubling of the Hubble time.

This result and the conclusion of Quinn & Zurek (1988) that halos tend to spin about the same axis at all radii together imply that the outer halo of many galaxies must be torquing the inner, visible galaxy about a direction that lies in its plane - if the inner galaxy is not torqued in this way it will not remain aligned with the outer galaxy.

How is the torque applied? There are two possibilities: by advection and gravitationally. That is, angular momentum may be carried inwards by accreting material such as the gas and stars of the Magellanic Stream (which contains more angular momentum than the Galaxy's disk), or by the gravitational field of the outer halo. Toomre (1983) and Dekel & Shlosman (1983) have considered warps induced by gravitational torquing. As regards advection, two questions arise: (a) To what degree is the advecting material concentrated into discrete blobs such as dwarf galaxies? (b) Are visible galaxies more affected by the baryonic or the dark component of advected material?

In CDM cosmogony small objects form first, and larger ones later as the result of mergers. So advected material is expected to come in lumps. Tóth & Ostriker (1992) have emphasized the vulnerability of disks to destruction by accreting lumps, so the existence of thin disks strictly limits the number of lumps that can penetrate to r 15 kpc in a galaxy such as our own, to one or two per Hubble time.

This limit does not restrict the number of lumps which can have flown by the galaxy without suffering sufficient tidal friction to spiral in before now. In fact it is possible that thin disks end abruptly as they do a few exponential scale lengths from their centers precisely because beyond this radius the frequency of intruders is too great to allow a decent stellar disk to accumulate. Given that the pericenter of the Magellanic Clouds is estimated to be 50 kpc (Murai & Fujimoto 1980) this does not seem implausible - the nearest close passage by a dark lump in 10 Gyr is likely to be significantly closer than the last pericenter of the fourth ranking member of the Local Group. Moreover, the outer disk of M31 is currently being disturbed by M32.

If the edge of the disk marks the radius at which intruders make the gravitational field too noisy for a thin disk to be possible, is it also the radius at which the inner galaxy begins to twist around towards the orientation of the outer halo?

This is a hard question to answer. On the one hand one would expect any twist in the galaxy/halo system that arises from the need to slew the current spin axis into line with the direction of freshly accreted angular momentum, to be concentrated towards the system's periphery, where the dynamical time is longest and therefore any given rate of slewing largest from a dynamical point of view. We have seen that the periphery must be reckoned to lie way out beyond 100 kpc. If the twisting were concentrated out there, it is hard to see how it could be noticeable as far in as 12-15 kpc.

On the other hand, infall puts material onto deeply plunging radial orbits, which is probably why Quinn & Zurek found angular momentum redistribution within halos so effective. Perhaps these plunging orbits successfully communicate the latest trends in infall right to the edge of the visible galaxy, which precisely fills the volume within which plunging orbits do not normally penetrate. Moreover, the disk behaves a bit like a gyroscope: it packs a lot of angular momentum into a small volume, so that its ratio of angular momentum per unit gravitational quadrupole is larger than that of the enveloping halo. ⁽³⁾ Hence the disk is harder to slew than the halo, and much of the twist between r = 0 and r = r_equi may be concentrated in the disk.

A thin, massive disk can transmit the torque required to reorient the spin of its inner rings without warping significantly; the disk will warp noticeably only where its surface density is unusually low (Ostriker & Binney 1989). In practice this means at its outer edge. The warp's line of nodes coincides with the axis of the torque. Deviations of the line of nodes from a straight line are associated with changes in the direction of angular momentum vector of currently accreting material.

One expects a certain amount of gas to be accreted alongside dark matter - probably a few percent of the whole. Exchanges of angular momentum between one parcel of gas and another of the same shell will be important as parcels sweep by each other in the region beyond r_equi. These exchanges will drive the angular momenta of individual parcels down towards the mean for the whole shell; this is essentially the process of settlement to a ring (Tohline et al. 1982; Quinn, 1991). Binney (1991) has estimated the typical radius r_circ of such a ring from CDM theory under the assumption that it settles within an isothermal halo with circular speed v_c = 250 km s^-1. The radii in question turn out to be large; r_circ 150 kpc. Gaseous disks are generally considered very much smaller than this. Why? One possibility is that 21-cm studies miss the outer parts of disks because they are too thin to be self-shielding against the cosmic UV flux. Indeed studies of L absorption, which can detect HI down to surface densities ~ 10¹⁴ cm^-2 compared with the threshold ~ 10¹⁸ cm^-2 characteristic of 21-cm studies, do routinely detect hydrogen more than 100 kpc from galaxies (Petitjean & Bergeron 1990).

Another consideration is that gas is prone to lose angular momentum to a triaxial halo and rapidly spiral inwards in a way that stars do not (Katz & Gunn 1991). So one cannot exclude the possibility that the edge of the gaseous disk is defined by the radius at which gas that recently fell in is settling to circular orbits. The outer disk would then not be perfectly aligned with the inner disk since its angular momentum would be more in line with the current fashion for the galaxy as a whole than that of the older disk.

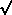
³ Specifically, _disk / _halo (32 / 9) r_h / R_d, where R_d is the scale length of the exponential disk, and the r^-2 halo, rotationally flattened to ellipticity , is assumed to be truncated by a factor e^{-r / r_h}. In reality the halo is probably not rotationally flattened, and _disk / _halo is probably still larger. Mathur (1984) has suggested that spiral structure arises from the large value of _disk / _halo.