B. Models for the Radio-to-X-Ray Spectrum and the Particle Lifetime Problem

It is virtually certain that the radio and optical emission are both produced by the synchrotron process. This is due to the high degree of polarization, and the similar polarization properties at these two bands (c.f. Sec. 2.B.). The cause of the X-ray emission is much less clear, and we now discuss several possibilities.

In principle, the X-ray emission could be thermal emission from small regions surrounding the knots. If we assume the largest emission region consistent with the knots appearing unresolved in the Einstein HRI images (~ 2"), and a temperature of 1 KeV, the observed X-ray luminosity of knot A requires a pressure of 1.4 x 10^-8 dyne cm^-2. This is much larger than the external pressure (Sec. 3.A.) so a thermal X-ray emitting region cannot be confined. Inverse Compton X-ray emission is also a possibility, but it is difficult to get enough X-ray luminosity from the observed radio-to-optical synchrotron spectrum; a large excess of infrared photons or low energy electrons ( < 100) must be invoked (BSH91).

X-ray synchrotron emission seems like the best possibility, though it is not completely without problems. The strongest evidence for X-ray synchrotron emission, is that the X-ray flux lies close to the extrapolated optical-ultraviolet spectrum for several of the knots (Fig. 14; BSH91; Sparks, Biretta, and Macchetto 1993). There is no evidence for it comprising a separate spectral component. Furthermore, the radio-to-X-ray spectra of the different knots have similar shapes, suggesting the X-rays are somehow related to the shorter wavelengths. The problems arise when attempting to model the shapes of the radio-to-X-ray spectra. All the knots show a spectral break near, or just below, optical frequencies. If we simply compare _ro to _ox we find the breaks range from ~ 0.5 for knot D, to ~ 0.8 for knots A, B, and C. These latter values are larger than produced by continuous particle injection models with synchrotron losses ( = 0.5, Kardashev 1962). And models with a sudden cessation of particle injection produce high frequency spectra which are too steep - ~ 1.67 (Pacholczyk 1970) or an exponential cutoff (Jaffe and Perola 1974).

A problem related to the high frequency spectra, is the short lifetime of the electrons producing the optical (and X-ray) synchrotron emission. The lifetime of these electron is short, and yet optical and X-ray emission is seen at large distances from the nucleus. The lifetime for a synchrotron emitting electron to lose its energy is proportional to

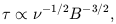
where is the observation frequency, and B is the magnetic field strength. Assuming equipartition fields, the lifetime of the radio emitting electrons is 10⁵ years, and the nucleus can supply radio emitting electrons to the entire source. However, at optical frequencies the lifetime is only ~ 100 years (and only ~ 10 years for the X-rays if they are synchrotron emission), and yet optical and X-ray emission is seen more than 3000 l.y. from the nucleus. Furthermore, the optical spectra of knots D, E, F, I, and A are all rather similar (Figure 9); there is no evidence for a systematic steeping with distance from the nucleus until after knot A. Several solutions have been proposed, though none seems without problems. First-order Fermi acceleration at shocks could re-accelerate the electrons (e.g., Rees 1978), however few of the knot look like shocks. For example, knots D, E, F, I, and A have similar spectra, but only A looks like a shock. A modification of this idea might be to have particle acceleration everywhere (from turbulent to shock regions), but acceleration models tend to give spectra which are strongly dependent on the compression ratio (Ellison, Jones, and Reynolds 1990). A different solution is to propose the energetic electrons are transported along the jet without radiative losses. In one version, OHC89 propose a low magnetic field "pipe" at the jet center which supplies the knots. A similar idea, is that the energetic electrons are propagated in a relativistic flow ( ~ 10) where time dilation prevents losses (Begelman 1992; c.f. Felten 1968, Meisenheimer 1991).