


The Sunyaev-Zel'dovich effect not only causes changes in the integrated
spectrum of
the CMBR, but also induces fluctuations in its brightness which appear
superimposed on the fluctuations arising from the formation of
structure in the early Universe
(Sec. 1.3). The angular
scale of these new structures in the CMBR will depend on their origin,
and on the large-scale structure of the Universe. Constraints on
both the manner in which clusters evolve and  0 have been
obtained by the limits to the fluctuation power from arcminute-scale
experiments.
0 have been
obtained by the limits to the fluctuation power from arcminute-scale
experiments.
The present review concentrates on the fluctuations induced
in the CMBR by clusters and superclusters of galaxies, but a diffuse
ionized intergalactic medium with density and velocity irregularities,
such as those created as large-scale structure develops, will
also produce significant CMBR fluctuations. The best-known of these
is the Vishniac effect
(Vishniac 1987),
which is due
to the kinematic Sunyaev-Zel'dovich effect of a perturbation in the
electron density
in the (re-ionized) diffuse intergalactic medium. Discussions of this,
and other, structures that are superimposed on the primordial spectrum
by inhomogeneities in the re-ionized intergalactic medium are given by
Dodelson & Jubas (1995)
for  0 = 1, by
Persi (1995)
for open Universes, and in the review of
White et al.
(1994).
0 = 1, by
Persi (1995)
for open Universes, and in the review of
White et al.
(1994).
Cluster Sunyaev-Zel'dovich effects can have a strong influence on the
CMBR because,
unlike ``normal'' astrophysical sources, the surface brightness of the
Sunyaev-Zel'dovich effect from a cluster is independent of redshift, and
does not suffer (1 + z)-4 fading. This is because the
effect is a fractional change in
the brightness of the CMBR, and the CMBR's energy density itself
increases with redshift as (1 + z)4, cancelling out
the dimming
effect of cosmology. The integrated flux density of a cluster at
observed frequency  ,
,
in the Kompaneets approximation, where j (x) is the Kompaneets
spectral function (defined by
which for a constant electron temperature over the cluster can be
written simply in terms of the total number of electrons in the
cluster, Ne, and the angular diameter and
luminosity distances, DA and DL, as
This indicates that the cluster's apparent luminosity increases as
(1 + z)4 - or, alternatively, that its flux
density is a function of intrinsic properties and angular diameter
distance only.
As a result, a population of clusters with the same Ne
and Te, observed at different redshifts, will exhibit
a minimum flux density at the redshift of maximum angular diameter
distance in that cosmology
(Korolyov et al. 1986).
Although this might provide a
cosmological test for
More detailed treatments of the effects of foreground clusters on the
CMBR express their results in the formalism of
Sec. 1.3
that is used to describe primordial fluctuations. A number of
different assumptions about the cosmology and evolution of large scale
structure have been used to calculate the
amplitude and angular pattern of the foreground fluctuations
(Rephaeli 1981;
Cavaliere et
al. 1986;
Cole & Kaiser 1988;
Schaeffer & Silk 1988;
Thomas & Carlberg 1989;
Markevitch et
al. 1992;
Makino & Suto 1993;
Bartlett & Silk 1994a,
1994b;
Ceballos & Barcons 1994;
Colafrancesco et
al. 1994;
see also the review by
Rephaeli 1995b).
A uniform result of the calculations
is that the distribution of sky brightness fluctuations that result
is strongly non-Gaussian and asymmetrical since it is composed of
negative or positive sources (depending on the frequency of
observation, and the sign of j (x)) with varying numbers of sources
on any line of sight or contained in a particular telescope beam
(e.g.,
Markevitch et
al. 1992).
However, the
amplitude and angular scale of the cluster-generated fluctuations
depend strongly on the pattern of cluster evolution and the cosmology
assumed. If the negative evolution of cluster atmospheres is strong
(negative n in the self-similar model used by Markevitch et al.;
eq. 128), then the distribution will be dominated by
low-redshift clusters and the value of
The angular pattern of fluctuations that results generally shows
significant power in the two-point correlation function
(eq. 8) at the level 10-6
If the evolution of clusters is to be studied in this way, then
observations of the cluster-induced Sunyaev-Zel'dovich fluctuation
pattern would
need to be made over a wide range of angular scales in order to
validate or falsify any one of the models unambiguously. This range of
angular scales overlaps that occupied by the stronger ``Doppler
peaks'' in the primordial spectrum of fluctuations, so that the
cluster signal may be hard to detect (see, e.g., the review of
Bond 1995).
The cluster signal is also an important
contaminant of the Doppler peaks, which are expected to be a useful
cosmological indicator and whose characterization is an important aim
of the coming generation of CMBR satellites (MAP and Planck).
Fortunately, measurements of the anisotropy pattern at several
frequencies can be used to separate Sunyaev-Zel'dovich effects imposed
by clusters and the primordial fluctuation background
(Rephaeli 1981):
the sensitivity required to achieve clean separations is
formidable, but achievable with the current baseline design of the
satellites' detectors.
An illustration of these results is given in
Fig. 27,
which shows the relative strengths of the power spectra of primordial
fluctuations, the thermal and kinematic Sunyaev-Zel'dovich effects, and the
moving-cluster Rees-Sciama effect in a
The sensitivity of the Sunyaev-Zel'dovich effect power spectrum to cosmology is
illustrated in Fig. 28
(Molnar 1998).
Variations of a factor > 10 in the power of fluctuations
induced by the thermal Sunyaev-Zel'dovich effect are evident at l >
300: although
this might be used as a cosmological test, the locations and strengths
of the Doppler peaks in the primordial anisotropy power spectrum are
more powerful. However, the amplitude of the Sunyaev-Zel'dovich effect power
spectrum depends on how clusters evolve, and measurements of this
power spectrum over a wide range of l should provide an important
test of models of the formation of structure in the Universe.
Superclusters of galaxies, and the gas pancakes from
which superclusters may have formed, are expected to make only a
minor contributions to the fluctuation spectrum
(Rephaeli 1993;
SubbaRao et al.
1994).
Once again, the angular scales on which the supercluster
signals appear are similar to those of the Doppler peaks, and both
good frequency and angular coverage will be needed to distinguish the
primordial and foreground signals.
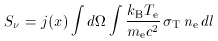
 n = y j (x) in equation 59),
x = h
n = y j (x) in equation 59),
x = h /
kB Trad is the usual dimensionless
frequency,
and the first integral is over the
solid angle of the cluster. Equation (129)
can be written as an integral over the cluster volume
/
kB Trad is the usual dimensionless
frequency,
and the first integral is over the
solid angle of the cluster. Equation (129)
can be written as an integral over the cluster volume
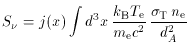
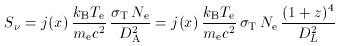
 0, in practice clusters exhibit a wide
range of properties and change significantly with redshift so it might
be difficult to distinguish the effects of cosmology, cluster
populations, and cluster evolution. The realizable cluster source
counts (the histogram of sky brightnesses observed by a particular
telescope of given properties) will then depend on a complicated mix of
observational characteristics of the telescope used, the cosmological
parameters, and the evolution of the cluster
atmospheres. Nevertheless,
Markevitch et
al. (1994)
suggest that a study of source counts at the µJy level (at
cm-wavelengths) or at the mJy level (at mm-wavelengths) can
constrain the spectrum of cluster masses (which determines the value of
y), the cosmological parameter
0, in practice clusters exhibit a wide
range of properties and change significantly with redshift so it might
be difficult to distinguish the effects of cosmology, cluster
populations, and cluster evolution. The realizable cluster source
counts (the histogram of sky brightnesses observed by a particular
telescope of given properties) will then depend on a complicated mix of
observational characteristics of the telescope used, the cosmological
parameters, and the evolution of the cluster
atmospheres. Nevertheless,
Markevitch et
al. (1994)
suggest that a study of source counts at the µJy level (at
cm-wavelengths) or at the mJy level (at mm-wavelengths) can
constrain the spectrum of cluster masses (which determines the value of
y), the cosmological parameter  0, and the redshift of cluster
formation. Using the results of arcminute-scale measurements of the
anisotropy in the CMBR (the OVRO RING experiment;
Myers 1990,
Myers et al.
1993),
Markevitch et al. were able to rule out
slowly-evolving (n = 1 in eq. 128) models in an open
Universe with
0, and the redshift of cluster
formation. Using the results of arcminute-scale measurements of the
anisotropy in the CMBR (the OVRO RING experiment;
Myers 1990,
Myers et al.
1993),
Markevitch et al. were able to rule out
slowly-evolving (n = 1 in eq. 128) models in an open
Universe with  0 < 0.3.
0 < 0.3.
 0 will not be
important. For slow evolution or no evolution, the value of
0 will not be
important. For slow evolution or no evolution, the value of  0
becomes important, since the variation of DA with redshift
dictates the appearance of the microwave background sky.
0
becomes important, since the variation of DA with redshift
dictates the appearance of the microwave background sky.
 <
<  T / T
>
T / T
>  10-5 on
sub-degree scales (e.g.,
Colafrancesco et
al. 1994),
but some models for the evolution
of clusters (and cluster atmospheres) can be ruled out from the
absence of large anisotropies in the OVRO data of
Readhead et al.
(1989),
Myers et al.
(1993),
or other experiments, and some
cosmological parameters can be excluded under particular models for
the evolution of cluster atmospheres. Since different models can make quite
different predictions for the angular pattern and the amplitude of
fluctuations, there is a potential for studying the processes that
lead to the accumulation of cluster atmospheres through a study of the
microwave background radiation on the range of angular
scales (arcminute to degree) on which the cluster signal should
be significant.
10-5 on
sub-degree scales (e.g.,
Colafrancesco et
al. 1994),
but some models for the evolution
of clusters (and cluster atmospheres) can be ruled out from the
absence of large anisotropies in the OVRO data of
Readhead et al.
(1989),
Myers et al.
(1993),
or other experiments, and some
cosmological parameters can be excluded under particular models for
the evolution of cluster atmospheres. Since different models can make quite
different predictions for the angular pattern and the amplitude of
fluctuations, there is a potential for studying the processes that
lead to the accumulation of cluster atmospheres through a study of the
microwave background radiation on the range of angular
scales (arcminute to degree) on which the cluster signal should
be significant.
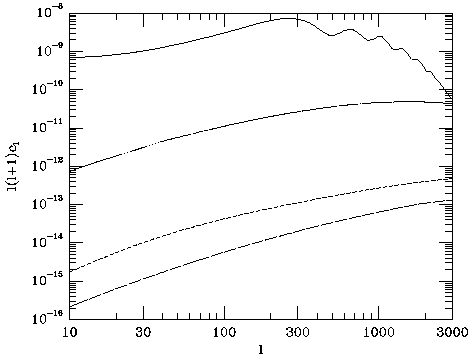
Figure 27. The zero-frequency power spectrum of primordial
microwave background
anisotropies (solid line; calculated using the CMBFAST code of
Zaldarriaga et
al. 1998),
the thermal Sunyaev-Zel'dovich effect
(dotted line), the kinematic Sunyaev-Zel'dovich effect (short dashed
line), and the Rees-Sciama effect from moving clusters (long dashed
line) predicted in the  -CDM
cosmology discussed by
Bahcall & Fan
(1998). Figure from
Molnar (1998).
-CDM
cosmology discussed by
Bahcall & Fan
(1998). Figure from
Molnar (1998).
 -CDM cosmology
(involving a significant cosmological constant and cold dark matter)
with an evolving cluster population
(Molnar 1998).
Although the details of the power spectra depend on the choice of cosmology
and the physics of cluster evolution (compare, e.g.,
Aghanim et al.
1998),
the general features are similar
in all cases. For l
-CDM cosmology
(involving a significant cosmological constant and cold dark matter)
with an evolving cluster population
(Molnar 1998).
Although the details of the power spectra depend on the choice of cosmology
and the physics of cluster evolution (compare, e.g.,
Aghanim et al.
1998),
the general features are similar
in all cases. For l  3000, the power spectrum is dominated
by the signal from primordial structures. The kinematic Sunyaev-Zel'dovich and
Rees-Sciama effects from the cluster population are a factor
3000, the power spectrum is dominated
by the signal from primordial structures. The kinematic Sunyaev-Zel'dovich and
Rees-Sciama effects from the cluster population are a factor
 102 less
important than the thermal Sunyaev-Zel'dovich effect. Thus the
evident detectability of the thermal Sunyaev-Zel'dovich effect
(Sec. 9)
is principally due to its strongly non-gaussian nature and its
association with clusters known from optical or X-ray observations,
and not to its intrinsic power. Future work, for example the all-sky
surveys that MAP and Planck will perform, will have the spectral
discrimination to detect the thermal Sunyaev-Zel'dovich effect on a statistical
basis, and should measure the power spectra of the thermal
Sunyaev-Zel'dovich effect
on small angular scales (l
102 less
important than the thermal Sunyaev-Zel'dovich effect. Thus the
evident detectability of the thermal Sunyaev-Zel'dovich effect
(Sec. 9)
is principally due to its strongly non-gaussian nature and its
association with clusters known from optical or X-ray observations,
and not to its intrinsic power. Future work, for example the all-sky
surveys that MAP and Planck will perform, will have the spectral
discrimination to detect the thermal Sunyaev-Zel'dovich effect on a statistical
basis, and should measure the power spectra of the thermal
Sunyaev-Zel'dovich effect
on small angular scales (l  300;
Aghanim et al.
1997;
Molnar 1998).
300;
Aghanim et al.
1997;
Molnar 1998).
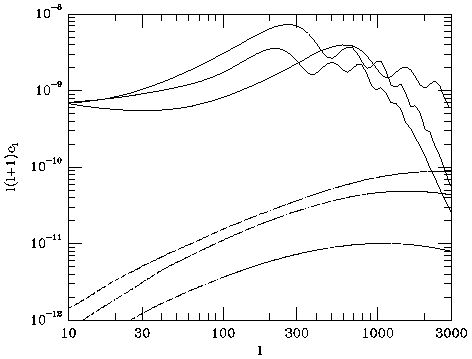
Figure 28. The zero-frequency power spectrum of primordial
microwave background
anisotropies (solid lines; calculated using the CMBFAST code of
Zaldarriaga et
al. 1998),
and the Sunyaev-Zel'dovich
effects of an evolving population of clusters (dotted lines) predicted
in three cosmological models consistent with the COBE anisotropies:
the open CDM,  -CDM, and
``standard'' CDM models discussed by
Bahcall & Fan (1998).
Figure from
Molnar (1998).
-CDM, and
``standard'' CDM models discussed by
Bahcall & Fan (1998).
Figure from
Molnar (1998).