5. The non-thermal Sunyaev-Zel'dovich effect

As was noted in Sec. 3.3, a non-thermal population of electrons must also scatter microwave background photons, and it might be expected that a sufficiently dense relativistic electron cloud would also produce a Sunyaev-Zel'dovich effect. Fig. 11, which shows a radio map of Abell 2163 superimposed on a soft X-ray image, indicates that in some clusters there are populations of highly relativistic electrons (in cluster radio halo sources) that have similar angular distributions to the populations of thermal electrons which are more conventionally thought of as producing Sunyaev-Zel'dovich effects. Indeed, in many of the clusters in which Sunyaev-Zel'dovich effects have been detected there is also evidence for radio halo sources, so it is of interest to assess whether the detected effects are in fact from the thermal or the non-thermal electron populations.

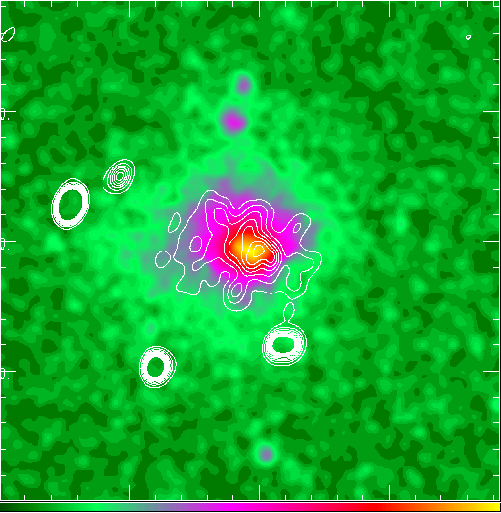
Figure 11. 1400-MHz radio contours superimposed on a soft X-ray image of Abell 2163 (Herbig & Birkinshaw 1995). Note the close resemblance of the radio and X-ray structures, and the diffuseness of the radio source. This is a particularly luminous example of a cluster radio halo source, with a radio luminosity Lradio 1035 h100-2 W.

so that the effect depends on the line-of-sight integral of the electron pressure alone. If a radio halo source, such as is seen in Fig. 11, and the cluster gas which (presumably) confines it are in approximate pressure balance, then this argument would suggest that the thermal and non-thermal contributions to the overall Sunyaev-Zel'dovich effect should be of similar amplitude if the angular sizes of the radio source and the cluster gas are similar. Since the spectra of the thermal and non-thermal effects are distinctly different (compare Fig. 7 and 8), the spectrum of the overall Sunyaev-Zel'dovich effect measures the energy densities in the thermal gas and in the radio halo source separately. This would remove the need to use the minimum energy argument (Burbidge 1956) to deduce the energetics of the source.

Matters are significantly more complicated if the full relativistic formalism of Sec. 3 is used. But this is necessary, since the electrons which emit radio radiation by the synchrotron process are certainly highly relativistic and the use of the Kompaneets approximation is invalid. Thus we must distinguish between the effects of the electron spectrum and those of the electron scattering optical depth, but the results of Sec. 3.3 can be used to predict the expected Sunyaev-Zel'dovich effect intensity and spectrum from any particular radio source.

Consider, for example the Abell 2163 radio halo, for which we assume a spectral index = -1.5 (there is no information on the spectral index, since the halo has been detected only at 1400 MHz: = -1.5 is typical of radio halo sources). The diameter of the halo is about 1.2 h₁₀₀^-1 Mpc, and the radio luminosity (in an assumed frequency range from 10 MHz to 10 GHz) is 10³⁵ h₁₀₀^-2 W. Using the minimum energy argument in its traditional form (see the review by Leahy 1990), the equipartition magnetic field is about 0.06 h₁₀₀^2/7 nT and the energy density in relativistic electrons is about 10^-15 h^1004/7 W m^-3. This estimate assumes that all the particle energy resides in the electrons, and that the source is completely filled by the emitting plasma. The equivalent electron density in the source is n_e = 2 x 10^-3 h₁₀₀^6/7 m^-3, which is a factor ~ 10⁶ less than the electron density in the embedding thermal medium and corresponds to a scattering optical depth of only 6 x 10^-9 h₁₀₀^-1/7, which is certainly much less than the optical depth of the thermal atmosphere in which the radio source resides. Although the power-law electron distribution is more effective at scattering the microwave background radiation than the intracluster gas, at low frequencies it is found that the predicted Sunyaev-Zel'dovich effect from the halo radio source electron distribution is T_RJ = -5 nK. This is about 10⁵ times smaller than the Sunyaev-Zel'dovich effect from the thermal gas.

The dominance of the thermal over the non-thermal effect from the cluster arises principally from the lower density of relativistic than non-relativistic electrons. Only a low relativistic electron density is inferred because of the high efficiency of the synchrotron process if only a small range of electron energies is present. If the frequency range of the synchrotron radiation is extended beyond the 10 MHz to 10 GHz range previously assumed, then the optical depth to inverse-Compton scattering depends on the lower frequency limit as _e 10^-12 h^-1/7 (_min / GHz)^-13/7 (which would be >> 1 if the electron spectrum extends down to thermal energies). A reduction in the lower cutoff frequency of the spectrum by a factor ~ 10³ then increases the estimated relativistic electron density to the point that the non-thermal Sunyaev-Zel'dovich effect makes a significant contribution. Indeed, this strong dependence of _e on _min or, equivalently, on the minimum electron energy, suggests that the non-thermal Sunyaev-Zel'dovich effect is a potential test for the low-end cutoff energy of the relativistic electron spectrum.

Thus although the original purpose of searching for the non-thermal Sunyaev-Zel'dovich effect (as was done by McKinnon et al. 1991) was to check on the applicability of the minimum energy formula, it is more appropriate to think of it as a measurement of the minimum energy of the electrons that produce the radio radiation. Although limits on this minimum energy can be deduced from the polarization properties of radio sources, these limits are model-dependent (e.g., Leahy 1990), and an independent check from the non-thermal Sunyaev-Zel'dovich effect would be useful.

The problem of detecting the Sunyaev-Zel'dovich effect from non-thermal electron populations is likely to be severe because of the associated synchrotron radio emission. At low radio frequencies, that synchrotron emission will easily dominate over the small negative signal of the Sunyaev-Zel'dovich effect. At high radio frequencies, or in the mm-wave bands, there is more chance that the Sunyaev-Zel'dovich effect could be detectable, but even here there are likely to be difficulties separating the Sunyaev-Zel'dovich effects from the flattest-spectrum component of the synchrotron emission.

Several inadvertent limits to the non-thermal Sunyaev-Zel'dovich effect are available in the literature, from observations of clusters of galaxies which contain powerful radio halo sources (such as Abell 2163) or radio galaxies (such as Abell 426), but few detailed analyses of the results in terms of the non-thermal effect have been possible, and a treatment of the interpretation of the Abell 2163 data is deferred until later (Sec. 9.2).

Only a single intentional search for the Sunyaev-Zel'dovich effect from a relativistic electron population has been attempted to date (McKinnon et al. 1991), and that searched for the Sunyaev-Zel'dovich effect in the lobes of several bright radio sources. No signals were seen, but a detailed spectral fit of the data to separate residual synchrotron and Sunyaev-Zel'dovich effect signals was not done, and the limits on the Sunyaev-Zel'dovich effects (of y 2 x 10^-3 for the best two sources) do not constrain the electron populations in the radio lobes strongly: the lobes could be far from equipartition without violating the Sunyaev-Zel'dovich effect constraint.

One difficulty with the analysis given above, and the discussion of the testing of minimum electron energy or the minimum energy formalism, is that radio sources are expected to be strongly inhomogeneous, so single-dish Sunyaev-Zel'dovich effect observations are averaging over a wide variety of different radio source structures (such as lobes and hot spots). This would mean, for example, that the spectral curvature that might be predicted by a superposition of the source spectrum and the Sunyaev-Zel'dovich effect might be also be produced by small variations in the electron energy distribution function from place to place within the radio source. If strong tests of the electron energy distribution are to be made, the observations must be made with angular resolution comparable with the scale of structures within the radio sources. For all but the largest radio sources (such as the lobes of Cen A), this means that interferometers (or bolometer arrays on large mm-wave telescopes) must be used. No work of such a type has yet been attempted, and the sensitivity requirements for a successful detection are formidable.