Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
311-358 Copyright © 1992 by Annual Reviews. All rights reserved |
where H0 = 100h km s-1
Mpc-1 is the Hubble constant. For
a source at redshift zs and a single deflector at redshift
zd,
we follow convention and set Dd = D(0,
zd), Ds = D (0,
zs), and Dds =
D (zd, zs). Elementary geometry
gives the lens equation (e.g.
Refsdal 1964a),
which connects the
source position
where the reduced deflection angle
which is a symmetric 2 x 2 matrix. This is not directly measurable,
but the relative magnification between two images, described by
the transformation matrix [µ(ij)] =
[µ(i)] [µ(j)]-1
can be estimated when the images are resolved. This is in general
nonsymmetric and provides four independent observables. The flux
magnification associated with the ith image is the absolute
value of the determinant of the magnification tensor,
i.e. µ(i) = | [µ(i)] |. For
unresolved images, only the relative flux
magnifications, µij =
| [µ(ij)] |, are measurable.
3. GRAVITATIONAL LENS OPTICS
3.1 Ray Deflections and the Lens
Equation
 0 in
which angular diameter distances
D (zi, zj) relate proper lengths
0 in
which angular diameter distances
D (zi, zj) relate proper lengths  j
located at redshift zj
to angles
j
located at redshift zj
to angles  i
subtended by these lengths when observed from
redshift zi < zj:
i
subtended by these lengths when observed from
redshift zi < zj:
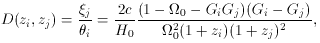
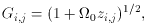
 and the image position
and the image position  (Figure 5),
(Figure 5),
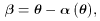
 (
( ) and
the true deflection angle
) and
the true deflection angle  hat (
hat ( )
are related by
)
are related by
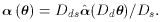
 hat =
hat = 
 / c2,
where
/ c2,
where  (
( ) is twice the
2D Newtonian potential obtained by solving the 2D Poisson
equation,
) is twice the
2D Newtonian potential obtained by solving the 2D Poisson
equation,  2
2  (
( ) =
) =  G
G (
( )
) (
( ). [A weak gravitational lens is, in its essentials,
equivalent to a flat space
deflector with refractive index 1 - 2
). [A weak gravitational lens is, in its essentials,
equivalent to a flat space
deflector with refractive index 1 - 2 / c2, where
/ c2, where  is
the 3D Newtonian potential with respect to infinity
(Eddington 1919).]
is
the 3D Newtonian potential with respect to infinity
(Eddington 1919).]
 for each image
position
for each image
position
 . However, the converse
is not true. For a nontrivial
deflection law
. However, the converse
is not true. For a nontrivial
deflection law  (
( ), it is possible to find more
than one solution
), it is possible to find more
than one solution  satisfying Equation 2 for a given
satisfying Equation 2 for a given
 , thus giving
rise to multiple imaging. (In
general, gravitational lenses are not like simple optical lenses which
have
, thus giving
rise to multiple imaging. (In
general, gravitational lenses are not like simple optical lenses which
have  hat (
hat ( ) varying linearly with
) varying linearly with
 .)
.)