


4.1. Special Relativity
Special relativistic gas dynamics (and MHD) is, in many respects, similar to its subrelativistic counterpart and many hydrodynamical effects like shocks, nozzle flow etc, carry over. In particular, it has recently been possible to demonstrate special relativistic, self-similar solutions of disk-driven, collimated outflow (Li, Chiueh & Begelman 1992, cf. Camenzind 1989, Lovelace et al. 1986). These solutions, typically, exhibit the property of equipartition between magnetic and mechanical energy asymptotically and arbitrarily large speed.
However, the surprisingly large effects of relativistic beaming imply that our observations of the powerful VLBI jets may be quite misleading although it is these that promise the finest probe of the jet collimation region. As we have already discussed, radiative drag becomes increasingly important in a particle-dominated flow with increasing bulk Lorentz factor. However, much larger bulk Lorentz factors are possible if most of the momentum flux, in the region where the radiation energy density is high, is in an electromagnetic form. Provided that the energy can be transported at high speed to the radio-emitting region there is no difficulty of principle in acquiring electrons from the surrounding gas and accelerating them to energies ~ 100 - 1000 MeV perhaps through shock waves. (Radio source models relying on this principle can have a beaming angle much larger than ~ c/vob and this may alleviate problems in accounting for the unbeamed sources.) Arguably, the most attractive way to produce an electromagnetically-dominated outflow is to extract spin energy from a Kerr black hole.
4.2. Black Hole MHD
As has been reviewed elsewhere (e.g.,
Thorne, Price &
MacDonald 1986),
it is also possible to extract the rotational kinetic energy of a
spinning black hole as well as that of
an accretion disk. A spinning black hole, described by the Kerr metric
can be described by two parameters (e.g.,
Misner, Thorne &
Wheeler 1973),
that can be chosen to be the
irreducible mass mi and the angular velocity
 . The irreducible mass is analogous
to the rest mass in ordinary relativistic dynamics and the minimum mass
to which a black hole can be reduced through classical processes. The actual
gravitational mass of
the hole m is related to the irreducible mass through the
familiar-looking formula
. The irreducible mass is analogous
to the rest mass in ordinary relativistic dynamics and the minimum mass
to which a black hole can be reduced through classical processes. The actual
gravitational mass of
the hole m is related to the irreducible mass through the
familiar-looking formula

where  =
2mi
=
2mi  < 2-1/2 in gravitational units. The mass difference, m -
mi, can be
extracted in principle. In practice, no more than half of this
difference is likely to be extracted, the balance going into the
irreducible mass.
< 2-1/2 in gravitational units. The mass difference, m -
mi, can be
extracted in principle. In practice, no more than half of this
difference is likely to be extracted, the balance going into the
irreducible mass.
Magnetic fields that thread the hole's event horizon and are supported
by external
currents will induce an electric potential difference between the poles
and the equator of
the hole. This will cause currents to flow. Fiducial numbers for ~
108 M black holes
in AGN are magnetic fields of strength ~ 104 G, potential
differences V ~ 1020 V and
currents I ~ 1018 A. At these large potentials, there
is ample electric field strength to
break down the vacuum and to create electron-positron pairs within a
black hole
magnetosphere. This allows current to flow continuously from the horizon
to infinity, while
particles move inward across the horizon, but outward at large radius in
a relativistic
MHD wind. Remember that only a negligible kinetic energy flux
need be associated
with those particles that are carrying the electrical current; the
overwhelming majority
would then be transported in the form of electromagnetic Pointing
flux. However, if
there is significant dissipation in the flow (and this is not an
unreasonable supposition),
then the mechanical energy flux may eventually dominate the outflowing wind.
black holes
in AGN are magnetic fields of strength ~ 104 G, potential
differences V ~ 1020 V and
currents I ~ 1018 A. At these large potentials, there
is ample electric field strength to
break down the vacuum and to create electron-positron pairs within a
black hole
magnetosphere. This allows current to flow continuously from the horizon
to infinity, while
particles move inward across the horizon, but outward at large radius in
a relativistic
MHD wind. Remember that only a negligible kinetic energy flux
need be associated
with those particles that are carrying the electrical current; the
overwhelming majority
would then be transported in the form of electromagnetic Pointing
flux. However, if
there is significant dissipation in the flow (and this is not an
unreasonable supposition),
then the mechanical energy flux may eventually dominate the outflowing wind.
This picture of electromagnetic energy extraction is reminiscent of (and
derived
from) theories of pulsar electrodynamics. However, there are some
crucial differences.
Firstly, there is the need for charged particle creation in the
magnetosphere and the
attendant dissipation. Provided that ions are extractable from neutron
star surfaces,
there is no necessity for this to occur, at least in simple
models. However, it is observed
that rapidly spinning, strong field pulsars, notably the Crab pulsar,
are quite dissipative
with at least several percent of the energy flux appearing as
 -rays. It is
reasonable to
guess that an even higher percentage of the extracted power might be
dissipated in this
manner in the case of black holes. (It is unlikely that the
-rays. It is
reasonable to
guess that an even higher percentage of the extracted power might be
dissipated in this
manner in the case of black holes. (It is unlikely that the
 3 GeV
3 GeV
 -rays detected by
the EGRET instrument on the Compton Gamma Ray Observatory originate directly
from a black hole magnetosphere as the opacity to pair production on ~
keV X-rays is much greater than unity. It is far more likely that these
-rays detected by
the EGRET instrument on the Compton Gamma Ray Observatory originate directly
from a black hole magnetosphere as the opacity to pair production on ~
keV X-rays is much greater than unity. It is far more likely that these
 -rays are formed
at greater distances from the hole, in an outflowing relativistic jet.)
-rays are formed
at greater distances from the hole, in an outflowing relativistic jet.)
A second important difference is that, unlike a neutron star, which is
an excellent
conductor, a black hole acts as if it possesses an electrical resistance
~ 100  . Indeed,
it is possible to develop a simple circuit analogy for a stationary,
axisymmetric magnetosphere (e.g.,
Thorne et al. 1986).
Consider two magnetic surfaces threading the
horizon and suppose that a current I flows out along one surface
and returns along the
other. The current will complete within the hole across an internal
resistance
. Indeed,
it is possible to develop a simple circuit analogy for a stationary,
axisymmetric magnetosphere (e.g.,
Thorne et al. 1986).
Consider two magnetic surfaces threading the
horizon and suppose that a current I flows out along one surface
and returns along the
other. The current will complete within the hole across an internal
resistance  RH and
at large distance from the hole by crossing a load impedance
RH and
at large distance from the hole by crossing a load impedance
 RL. Let the magnetic
flux enclosed by the two surfaces be
RL. Let the magnetic
flux enclosed by the two surfaces be

 .
There will be more magnetic field outside
these two surfaces along which current will also flow. It is possible to
ascribe an angular
velocity
.
There will be more magnetic field outside
these two surfaces along which current will also flow. It is possible to
ascribe an angular
velocity  to the magnetic field
lines (essentially the angular velocity of a local observer
who measures no electric field). This will be a weighted average of the
hole (
to the magnetic field
lines (essentially the angular velocity of a local observer
who measures no electric field). This will be a weighted average of the
hole ( H) and
load (
H) and
load ( L) angular
velocities.
L) angular
velocities.
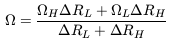
We might expect that  L = 0, but if the magnetic surface intersects the
accretion disk
then it will be non-zero. It can then be shown that the torque that is
transmitted from the hole to the load by the magnetosphere is
L = 0, but if the magnetic surface intersects the
accretion disk
then it will be non-zero. It can then be shown that the torque that is
transmitted from the hole to the load by the magnetosphere is

Rearranging this equation, we obtain an energy conservation equation.
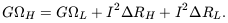
In other words, the work that it is done by the hole on the magnetosphere equals the work done by the magnetosphere on the load plus the ohmic dissipation in both the hole and load. The ohmic dissipation in the load can be large enough to satisfy the non-thermal and dynamical appetites of relativistic jets and double radio sources.
Therefore, in this model, the power derives hydromagnetically, apparently from
within the horizon. This has led
Punsley & Coroniti
(1990)
to suspect that causality
is violated and that it is not possible for a black hole to evolve from
generic initial
conditions to this steady state. (In the case of a pulsar, there is no
such problem because
the neutron star is definitely causally connected to its magnetosphere.)
However, an alternative view (e.g.,
Blandford 1990)
is that the causal connection between the hole
and its magnetosphere is provided gravitationally by the frame-dragging
effect of the
g0 components of the metric tensor. It has not yet been possible to resolve
this dispute
satisfactorily by solving a suitable characteristic initial value
problem completely.
components of the metric tensor. It has not yet been possible to resolve
this dispute
satisfactorily by solving a suitable characteristic initial value
problem completely.
4.3. Boundary Layers
At first sight, the differences between black holes and protostars seem so great that it is surprising that they could play a common role in jet formation. However, I want to argue that there is an analogy that can be exploited. Specifically, if a protostar is orbited by an accretion disk which extends down to its surface (and this requires that the stellar magnetic field not be too great), then a boundary layer should form (e.g., Torbett 1984, Pringle 1989). As long as the star is not rotating with close to the break up angular velocity, (and observations of T Tauri stars suggest that this may be the case, though see Shu et al. 1988 for an alternative view), then half of the total gravitational binding energy released by infall onto the star will come from the boundary layer.
The structure of a boundary layer is still a matter for vigorous debate (e.g., Tylenda 1981). However, provided that much of the power is released as heat (or as radiation which can be absorbed by the surrounding gas), then it will function rather like a spinning black hole in an AGN. Specifically, I propose that most of the power carried by jets is concentrated in the central core and is associated with the central object. In the absence of a confining disk wind, this energy release would probably escape quasispherically. Similar boundary layers can form in CV and XRB, and these may also influence outflows in these objects.
4.4. Powers of Ten
There may be one further key ingredient for the production of a highly
collimated
jet. It may be necessary that the magnetic flux thread the disk over
several decades of
radius. As can be seen from Table 1 (cf.
Ray, Marscher, these proceedings), there is no
example of a jet that has to be finely collimated within a distance
 103 the putative
size of the central object. Indeed, if a jet originates from a disk
extending over several
decades of radius, its velocity structure is probably far more complex
than popularly
assumed and its degree of collimation at fixed altitude will decrease
with increasing cylindrical radius.
103 the putative
size of the central object. Indeed, if a jet originates from a disk
extending over several
decades of radius, its velocity structure is probably far more complex
than popularly
assumed and its degree of collimation at fixed altitude will decrease
with increasing cylindrical radius.
| AGN | YSO | XRB | CV | |
| Vj/c | 1 | 10-3 | 0.3 | 10-2 |
| Lj | 1044 | 1035 | 1040 | 1033 |
| M | 108 | 1 | 10 | 1 |
| R | 1014 | 1011 | 106 | 109 |
| Vesc/c | 1 | 10-3 | 0.3 | 10-2 |
| Rcoll | 1017 | 1016 | 1011 | 1011 |
| B | 104 | 103 | 109 | 106 |
In the case of an AGN, the outermost sheath may move comparatively slowly with speed ~ a few hundred km s-1 and be quite poorly collimated. In addition, it may eventually be braked by interaction with the surrounding interstellar medium. Interior to this sheath may be approximately axisymmetric magnetic surface twisting and expelling matter with increasing speed roughly some multiple of the Keplerian speed of the disk at the magnetic footpoints. Material expelled from the inner disk will travel at mildly relativistic speed. Finally, there may be ultrarelativistic energy release from the black hole itself. This should be responsible for the superluminal motion. Likewise in a YSO, the optical jets, on this interpretation derive most of their power from the boundary layer and perhaps the innermost parts of the accretion disk; the molecular and fast neutral components, being associated with the outer disk.
It is important to compare the powers, thrusts and torques that may be
associated
with different decades of radius. For an AGN accretion disk extending
over at least five
decades of radius, the angular momentum that must be released at the
largest radii is
at least 300 times that from the inner disk. (It may be considerably
larger if most of the
angular momentum is transported through the disk or the gravitating mass
increases
with radius.) By contrast, most of the binding energy is released at
small radius. For
the thrust, the answer is less clear cut, though. If the magnetic field
and gas density
follow the self-similar scaling B
 r-5/4,
r-5/4,

 r-3/2,
then the thrust per decade will
decrease
r-3/2,
then the thrust per decade will
decrease  r-1/2. If this law is followed, then we expect that
the innermost parts of
the jet are able to accelerate the surrounding outer jet to relativistic
speed. Conversely
if there is a deficit of momentum release from the inner disk, then the
asymptotic jet
speed will be characteristic of the escape speed from the outer
disk. Perhaps this offers
an explanation for the apparently bimodal behavior of extragalactic
radio jets. The low
power, slow Type 1 jets derive mostly from the outer disk; the fast,
powerful Type 2
jets from the inner disk. Perhaps it is necessary for there to be a
rapidly spinning black
hole for a Type 2 jet to form and we might expect that a declining AGN
would evolve
from Type 2 to Type 1. An analogous evolution might be anticipated in
the case of YSO.
r-1/2. If this law is followed, then we expect that
the innermost parts of
the jet are able to accelerate the surrounding outer jet to relativistic
speed. Conversely
if there is a deficit of momentum release from the inner disk, then the
asymptotic jet
speed will be characteristic of the escape speed from the outer
disk. Perhaps this offers
an explanation for the apparently bimodal behavior of extragalactic
radio jets. The low
power, slow Type 1 jets derive mostly from the outer disk; the fast,
powerful Type 2
jets from the inner disk. Perhaps it is necessary for there to be a
rapidly spinning black
hole for a Type 2 jet to form and we might expect that a declining AGN
would evolve
from Type 2 to Type 1. An analogous evolution might be anticipated in
the case of YSO.
4.5. Precession
Another important clue comes from precessing jets. The most prominent example is SS433 (Vermeulen, these proceedings, Peter & Eichler 1992, preprint) although there is some doubt in this case that the physical environment is typical of jets. Less clear-cut examples of inversion symmetric sources can be found in the extragalactic radio astronomers' œuvre, although it is not clear whether or not this morphology is attributable to precession, alignment or chance in most cases. If either precessional or aligning torques are at work, then this provides additional evidence that jet collimation occurs over many decades of radius.
The simplest explanation for jet precession, e.g., in SS433, invokes the "hotplate" model and posits that the companion star has a driven precession with a 164d period and that the accretion disk is slaved to this, perhaps in antiphase. A modulation at half of the orbital synodic period (~ 6.3 d) supports this interpretation. One objection that has been raised, though, is that the inflow timescale from the outer disk is not short compared with the precession period and so we might expect that the inner disk has a substantial phase lag with respect to the outer disk. There may, however, be a resolution of this difficulty if, as outlined above, it is poloidal magnetic field, attached to the outer disk, that is responsible for the collimation, while most of the power and thrust (and consequently the jet speed) is controlled by the inner disk.