1.1.4. Towards the Physical Universe

Newton's fundamental insight into nature allowed the discovery of the R^-2 force law of Universal Gravitation. From this, Kepler's laws follow trivially. We can readily derive Kepler's third law from Newton's equations as follows:

Assume that M₁ is a small mass in a circular orbit about a much larger mass M₂. We can write down the Force law on M₁ using Newton's formulations:

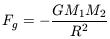
	(1)
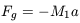
	(2)

Combining terms yields:

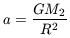
(3)

In an orbit governed by a central force, the centripetal acceleration is given by

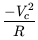
(4)

For a circular orbit, the circular velocity, V_c is just the 2 R / P , where P is the orbital period. Equating 3 and 4 and writing V_c in terms of R and P then yields

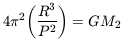
(5)

in which the harmonic law of Kepler is now apparent as the R³ / P² term. Measurements of R and P for any lesser body (M₁) in orbit about a larger body (M₂) now gives directly a physical quantity, mass.

The above derivation, however, assumed some physical insight in the form of equation 4. The genius of Newton was his ability to use calculus and coordinate transformations to reveal the underlying physics. For example, equation 4 is really derived using the following coordinate transformation appropriate for an object in a circular orbit.

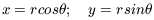
(6)

Newton defines the first time derivative of a spatial coordinate as a velocity and the second time derivative as an acceleration. An object in circular orbit has a constant acceleration in the r and directions. Differentiation of equation 6 yields

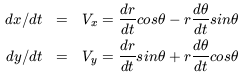
(7a)

A second differentiation with respect to time now yields

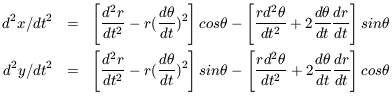
(7b)

and the accelerations in the r and directions now are just

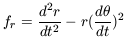
	(8a)
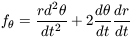
	(8b)

For a circular orbit d²r / dt² is zero so that

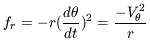
(9)

and equation 4 is recovered.

Newton's ability to predict Kepler's laws signifies the arrival of the first physical cosmology. Such a cosmology is defined by the ability of (unbiased) observation to provide information and insight into the physical properties of objects that inhabit the Universe. For Newton, these physical properties were mass, position, velocity, acceleration, energy and momentum. Objects with those properties would interact to define the Universe and the interaction mechanism was gravity.