2.3.2. The Second Rung: Distances to stellar clusters

Stellar clusters are important empirical astrophysical laboratories since they represent a group of stars at a common distance which were born at a common time. Differences in stellar evolutionary rates then allow the HR diagram to be filled out after a few million years of stellar evolution. Let's suppose that intermediate age stellar clusters, which contain a few thousands of stars, contain a certain type of star that can serve as a standard candle but that this certain type of star is not contained in the currently available trigonometric parallax samples. Let's further suppose that this star is intrinsically bright and hence can be seen to large distances. If we can then determine the distance to the cluster containing that star we can then calibrate its absolute brightness. We can then use that star to probe larger distances.

There are basically three types of stars found in stellar clusters that are useful to determine distances in our own galaxy as well as in external galaxies. These stars are:

RR Lyrae variable stars. These variable stars typically have pulsational periods of a few days and there is no correlation between pulsational period and luminosity. These stars are evolved stars and are found in the oldest clusters, like globular clusters. Although there is still some disagreement over their absolute magnitude (more fully discussed below), these stars have M_v +0.5 and hence can be used as a distance indicator out to a distance of 1 Mpc at which point they have an apparent magnitude > 25.0 mag, the limit of ground-based telescopes.

Cepheid Variable stars. These variable stars show a strong relationship between intrinsic luminosity and pulsational period. In practice, this relationship is empirically defined by Cepheids in the Large Magellanic Cloud (LMC) and hence an accurate distance to the LMC would calibrate the relationship. However, there is some concern that the Cepheid Period-Luminosity relationship has a dependence on metallicity and hence the LMC relationship may not be universal. Cepheids are also found in young, open clusters in our Galaxy but, as we shall see, calibrating their intrinsic luminosity in those clusters is quite difficult. For the longer period Cepheids (periods of a month or so) the intrinsic luminosity is quite large, M_v -7. Hence, ground based measurements can detect this population out to a distance of 4 Mpc. However, the improved angular resolution available with HST has allowed individual Cepheid Variables to be detected out to distances of 15 Mpc.

In January 1997 a conference was held in which some of the first Hipparchos results were made public and discussed. The most relevant of these new results comes from Feast and Catchpole who discuss a parallax sample of 26 Cepheids. These stars are at the very limit of the useful range of accurate parallax measurement of Hipparcos and therefore the measurements are potentially subject to systematic error. Notwithstanding this, Feast and Catchpole derive a zero point for the Cepheid PL relation which is approximately 0.2 mag brighter than previous measurements indicate. This has significant consequences for the Cepheid distance scale that we describe later in this chapter. However, there is still much uncertainty in this new zeropoint estimate as 1) there may be systematic errors in the parallax measurements themselves for these large distances, 2) Feast and Catchpole derive reddening estimates to the Cepheids based only on Blue and Visual photometry, 3) they assume a metallicity correction of -0.04 mag where the correction comes from the Laney And Stoble (1992) metallicity calibration and the metallilcity of the individual Cepheids is inferred from the B-V color. Unfortunately, the reddening and metallicity corrections are degenerate when only B-V is used. Hence, this apparent change in the zeropoint of the Cepheid PL relation requires additional confirmation.

The brightest Red Supergiants. These are young massive stars which are in a short-lived evolutionary phase at the tip of the Red Giant branch. There luminosities can approach M_v = -9 and hence ground based measurements can detect them in Virgo cluster galaxies and beyond.

To take advantage of these stellar distance indicators one has to accurately calibrate their absolute magnitudes by measuring good distances to nearby clusters which contain these objects. In the case of RR Lyraes, this means globular clusters and there essentially are no nearby globulars. For Cepheids and M-supergiants, young, open clusters contain a handful of these objects. These clusters are generally located in the plane of the Galaxy and hence are reddened by interstellar dust.

Main Sequence Fitting

This method relies on using the intrinsic luminosity of the main sequence (in practice the lower main sequence). Since stars in a cluster are at a common distance then differences in apparent magnitude reflect differences in intrinsic luminosity. If enough of the main-sequence can be detected, then its possible to fit that sequence in apparent magnitude space with the calibrating sequence obtained from trigonometric parallax. This is schematically shown in Figure 2-2. In principle this method should be very good as there are a large number of stars used in the fit and hence the zeropoint errors are formally small. A hidden assumption in this fitting procedure is that the shape of the main sequence is the same as that of the calibrating sample of stars. To first order, this is a safe assumption. To second order, differences in metal abundance and age slightly affect the shape and placement of the main sequence depending upon what filter system is used to measure effective temperature.

Figure 2-2: Schematic Representation of main-sequence fitting. Here the calibrated main-sequence is plotted in absolute magnitude space, where the absolute manitudes of the lower main sequence stars, shown as a solid line, have been calibrated from trigonometric parallax samples. The rest of the main sequence is represented by a dashed line indicated that very few of these stars are in the available parallax samples. The hypothetical lower main sequence of a nearby cluster is shown. The offset with respect to the calibrating relationship is 7 mags which is a distance of 250 parsecs. Note in this representation, the lower main sequence is fairly vertical meaning that small errors in determining the spectral type of a star translates into significant error in distance.

As schematically shown in Figure 2-2, in the traditional B-V vs V CM-diagram, the lower main sequence is quite vertical and it is the horizontal offset that determines the distance. This means that the spectral type or surface temperature of the stars that comprise the lower main sequence in the stellar cluster must be quite well known otherwise large random errors can be introduced. For instance, a change of just one sub-spectral class type (e.g., G8 vs G9) introduces an error of 12% in the distance. It is therefore much better to use a color system in which the main-sequence is relatively flat so that errors in spectral classification are not so severe. This can be done if a long baseline color index, such as V-K is used. Until recently, this was not practical but now with relatively large format IR arrays coming on line, these important measurements can be done.

There are two important limitations to deriving distances to nearby stellar clusters via main-sequence fitting.

1) The calibration of main sequence luminosities, from the parallax samples, is most reliable for stars with masses less than that of the sun. These so-called red dwarfs have absolute magnitudes in the range M_v +6-+10. Hence, even at a distance of 1 kpc, the bottom end corresponds to an apparent magnitude of +20. At this faint of flux level it is difficult to accurately measure an apparent magnitude.

2) Star formation in our galaxy generally occurs within the confines of dusty molecular clouds. Newly formed clusters are often surrounded by a cocoon of dust. After a million years or so, the young cluster has migrated out of this dusty cocoon but is still located in the plane of our galaxy. Nearby clusters have relatively large angular sizes on the sky (e.g., the radius of the Pleiades cluster is 4 degrees) Over this angular extent, the amount of foreground reddening will vary across the face of the cluster and hence systematic errors will result if a single reddening determination is made. In addition, again because of the large angular size, the only feasible manner of doing stellar photometry is via photographic plates as wide field CCD imaging systems are a rather recent development. Thus, the available photometry is mostly photographically based with reddenings to individual stars that are not well determined.

Convergent Point Method

Distances to some nearby clusters can also be determined using a second method which takes advantage of the fact that open clusters are only weakly gravitationally bound so that the individual stars are gradually escaping and the cluster is essentially expanding. If one can determine the true space motion of the individual stars, by measuring the radial velocity and proper motion components, the individual vectors will point back towards a region of small radius. This point is known as the convergent point and a distance estimate to the cluster can be done as follows:

For sufficiently nearby stars, the transverse component of their velocity can be measured over periods of decades. This motion is usually measured in seconds of arc per year. If we denote the proper motion by µ and the true transverse velocity by T and the parallax of the star (measured in seconds of arc) by _p then the quantity µ / _p is equal to T in units of astronomical units per year. One astronomical unit per year is equivalent to 4.74 km/sec. Therefore

(1)

and the true space velocity of any star is

(2)

We can then apply the convergent point method (also known as the moving cluster method) to the Hyades cluster. Referring to Figure 2-3, V_h is the true space velocity of the Hyades cluster which is deconvolved into T and V components. Each individual star has some angle between the sun and the extrapolated convergent point. This geometry then permits the following:

(3)

Solving for _p yields the distance

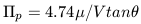
(4)

Figure 2-3: Schematic representation of the Convergent Point Method. The individual stars (small black circles) are moving on the plane of the sky in a roughly parallel trajector which points towards a common point, the convergent point denoted by the filled square. If the angle between the convergent point and an individual star can be measured, since determining the radial and tangential components to the velocity will yield a distance, as derived in the text.

Figure 2-3a: Color photograph of the Pleideas Cluster. From Jason Ware. The scattered blue light is from dust associated with the cluster. Correcting the stellar luminosities for the presence of dust is one of the outstanding problems in using clusters for main-sequence fitting and subsequent distance derivations.

The Pleiades is approximately twice as far away as the Hyades and is a more metal-normal cluster. This provides a better calibration of main sequence luminosities. Distances to the Pleiades can be determined by main-sequence fitting to the few A and F stars that are in the trigonometric parallax sample. Unfortunately, the resulting distance modulus depends upon which parallax sample is used and whether or not Lutz-Kelker corrections should be applied. Lutz-Kelker (Lutz and Kelker 1975) corrections are rather important and occur for the following reason. If there is a uniform distribution of stars (a reasonable assumption for nearby stars) then the number of stars varies as distance cubed. Each determination of trigonometric parallax has an associated error. Thus, if you define a distance limited sample (say all stars with measured trig. parallax 0.05 arcseconds or greater) then some stars with larger distances will scatter into your sample (because of measuring errors) and some stars with smaller distances will scatter out. Because there are more stars at larger distance, the net effect is that your sample to be contaminated by more distant stars and your estimation of intrinsic luminosity will be systematically low. For extragalactic samples, the same problem is present and is commonly known as the Malmquist effect. This effect is shown in Figure 2-3.

The Lutz-Kelker method offers a statistical correction for this effect and should always be applied. It is rather unclear why some authors do not apply it. Due to these effects, determinations of the distance modulus (m - M = 5 log (r / 10) where r is measured in parsecs) of the Pleiades varies from 5.57 ± 0.08 to 5.68 ± 0.04. Proper motion studies of the Pleiades members are more difficult but yield distance moduli that are consistent with these estimates. Nonetheless, this is a 10% range in the distance to the Pleiades which ultimately becomes part of the error in determining H₀.

Using the distance to the Hyades or Pleiades, combined with the ground-based trigonometric parallax sample, in principle, now gives us the entire range of main-sequence luminosities which we can use to derive distances to clusters that actually contain Cepheid variable stars. The typical distance to a cluster like this is a few kiloparsecs. If we consider a young cluster at a distance of 3 kpc (m - M = 12.4) then the sun would have an apparent V-magnitude of 17.2. Using a CCD device, 1% photometry at this brightness level is easy, but with photographic photometry it is not. This is why it is essential to involve A and F stars in the main-sequence fitting, as such stars would be in the magnitude range 12-15 where precision photographic magnitudes have already been obtained. In general, accurate photometry of lower main sequence stars, where the calibration is most secure, does not exist in distant, young Galactic clusters that contain Cepheids.