3.2.2. Clusters of Galaxies

These are prominent structures which are easily identified on large scale photographic plates. The best studied nearby rich cluster is the Coma cluster of Galaxies shown in Figure 3-3. Clusters of galaxies are subjectively classified according to a "richness" criteria. This criteria is basically the number of "bright" galaxies that appear within a fixed angular radius on the Palomar or ESO Sky Survey plates. A typical cluster detected in this manner has 100-1000 "bright" galaxies. Based on this somewhat loose criterion, George Abell and collaborators have cataloged approximately 4500 clusters of galaxies (see Abell et al. 1989). While some of these cataloged clusters are not real but instead accidental projections of groups along the line of sight, most are gravitationally bound units. These clusters of galaxies generally have three components, although only two of them are accounted for in the typical fit of the cluster density profile:

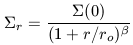
(6)

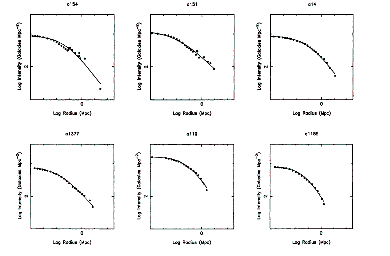
where (0) is the central surface density of galaxies, r₀ is the core radius and is the slope of the power law that characterizes the radial fall off in surface density, _r. Figure 3-4 shows a selection of surface density profiles for clusters. The three structural components of clusters are:

Figure 3-3: CCD image of the center of the Coma Cluster, the richest nearby cluster. The center is dominated by many elliptical and SO galaxies.

Figure 3-4: A sample of cluster density profiles showing the variations in the outer fall off. Data come from West and Bothun (1990).

1. A core (r₀) - this is a region where the projected surface density of galaxies is relatively flat. Not all clusters exhibit this feature. For those that do, the central densities can be quite high. These densities can be estimated by measuring (0), r₀ and the central velocity dispersion. For an isothermal sphere, the relation between r₀ and ₀ is:

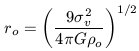
In the case of Coma the core radius is 300 kpc and the central density is 0.008 M pc^-3. This central density is 10⁵ - 10⁶ times higher than the average density of the Universe. In this high density region, spiral galaxies are almost never found.

2. The region - this is where the surface density profile begins to fall off. In practice, one can define the "cluster" as the radius which encloses a density contrast of 100. This radius depends upon the slope in equation 6. Clusters of galaxies show large variations in this slope. Some have very extended regions that contain many galaxies while others have sufficiently step profiles that most of the galaxies are contained in the r₀ region. If the cluster contains any spiral galaxies they will most likely be found outside of this region.

3. The infalling region - while not normally viewed as a structural component to clusters, we discuss it here because delayed infall from this region will augment both the r₀ and regions over a Hubble time. Most of the infalling galaxies will be spirals. This infall causes slow evolution of the density profile as cluster relaxation times are long (see below). Without accurate distances, however, it is impossible to determine which galaxies are in the region and which are still infalling.

Evidence that Clusters of Galaxies are Gravitationally Bound

Evidence that clusters of galaxies are gravitationally bound comes in a variety of forms:

1. The galaxy density is quite high and leads to values of over density in the range 100-1000. This range of overdensity is sufficient for the velocities of member galaxies to become virialized. The typical 3D velocity dispersion is 1500 km s^-1 whereas the expansion velocity over the scale of the cluster is 100-200 km s^-1.

2. Most clusters are sources of intense X-ray emission with typical temperatures of 2-10 Kev. Such high temperatures are best obtained as a result of gas in hydrostatic equilibrium with respect to a deep gravitational potential. This X-ray emission is also well bounded and usually has a density profile that falls off in a manner similar to, or slightly shallower than, the galaxy surface density profile (although we note that cluster X-ray profiles are somewhat hard to measure due to low S/N in the X-ray data).

3. Deep CCD surveys of the sky have shown the existence of clusters of galaxies at z 1 that look very much like the present-day core of the Coma cluster (see Castander et al. 1994; Postman et al. 1996). This indicates that a) some rich cluster cores did form early-on and b) in these rich clusters there has been little evolution of the core population over the last few billion years. This is not to say that augmentation of cluster cores by delayed infall is not occurring, but rather that, out to z = 1 you can find examples of cluster cores which are as dense as that seen in Coma.

Cluster Timescales

There are several relevant timescales associated with clusters of galaxies and they include the following

Dynamical Time Scale: This can be thought of as the time it takes for the cluster to communicate with itself through its own potential. There are many different ways to estimate this time scale but they all scale has _clust^-1/2, which is essentially the gravitational free-fall time. The most convenient way to define the dynamical timescale is in terms of the crossing-time. This crossing time is

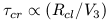
(7)

where R_cl is the characteristic cluster radius and V₃ is the three dimensional velocity dispersion. For any system of mass particles influenced by small larger scale potential, application of the Virial Theorem can be done after 1 dynamical timescale has elapsed. This allows the systems mass to be estimated from R_cl and V₃ as

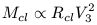
(8)

For a spherical system

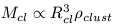
(9)

Substituting this into equation 8 yields

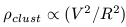
(10)

meaning that R / V _clust^-1/2. This result can also be arrived by considering the time it would take for a sound wave to cross the cluster or the timescale of gravitational free fall collapse. Equation 11 below is a convenient parameterization of the dynamical timescale in terms of observables:

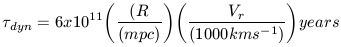
(11)

where V_r is the radial component of the three-dimensional velocity dispersion. A typical cluster has R = 1 and V_r = 1000 km s^-1 which leads to _dyn ~ 10⁹ years or roughly 10% of the expansion age.

Relaxation Timescale: The relaxation timescale is the characteristic timescale over which equipartition of energy among all the particles in the potential occurs. In such a situation mass segregation occurs with the lighter galaxies having larger v than the heavier galaxies as all galaxies have the same value of 1 / 2mv². As the mass range for "bright" cluster galaxies is 100, the corresponding range in v would be 10. Thus mass segregation should be relatively easy to verify as a cluster of galaxies would exhibit their brightest galaxies in the cluster core and the fainter galaxies preferentially on the outside. Relaxation can also dynamically heat the very lightest galaxies to escape velocity. To date there has been no convincing evidence that mass segregation in any cluster has occurred. While some clusters (see below) are dominated by a central massive galaxy which continues to grow as a result of the assimilation (cannibalism) of other cluster members, this is not a relaxation effect. The lack of observed mass segregation helps constrain the overall ages of clusters of galaxies.

Relaxation is motivated by two kinds of interactions: short range two-body encounters between the individual cluster members and long-range forces due to the smooth cluster potential. In a gravitating system of N-bodies there are two reasonable physical limits that can be described: 1) For small N, a body clearly moves through a field in which the mass is concentrated in the other N-1 bodies or 2) For large N the potential is smooth as it is a mean potential generated by all the other particles. For clusters of galaxies, it is unclear if they are in the limit of large or small N.

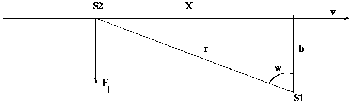
In the case of large N, we can derive an expression for the relaxation timescale by considering a system of equal mass particles moving through a smooth potential. In this case, we now show that the relaxation timescale increases with increasing N. Figure 3-5 specifies the encounter geometry of two equal mass objects (assumed to be point masses) that gravitationally scatter off one another. For the sake of this derivation, consider the objects as stars and the potential as a collection of equal mass stars (e.g., a galaxy). The physical question we wish to address is what happens to a star as it orbits around a galaxy at some radius and gravitational scatters off of other nearby stars and hence has its velocity perturbed.

Figure 3-5: Encounter geometry for two stars which gravitationally scatter of off one another.

For this approximation we consider all encounters to be small, that is v / v << 1. In this case we can consider the perturbing star, S1, to remain stationary and that the perturbed star, S2, remains on a straight line trajectory. From the geometry of Figure 3-5 we can then specify the force law as

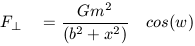
(12)

or since cos(w) = b/r then

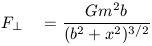
(13)

We now set the distance X to be vt so that

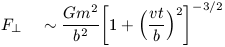
(14)

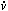
Remembering that Newton says F = m and setting s = vt/b (ds / dt = v / b) and integrating over all time then yields

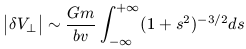
(15)

which can be evaluated to yield

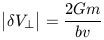
(16)

where we see that the perturbation in velocity depends on the initial mass and velocity of the perturbed star and its minimum distance from the perturbing star, which one might have guessed a priori.

Now consider a galaxy of radius R. The surface density of stars in that galaxy is N / R². Upon one orbit of the galaxy the star has a number of encounters, n, with impact parameters in the range b to b + db specified by the following

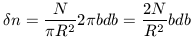
(17)

The total number of encounters would be obtained by integrating over db so note that if the range of db was from 0 to R one would recover n = N. Since the perturbations are randomly oriented then < v > = 0 We are interested in the amplitude of v so that

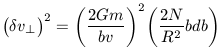
(18)

This expression is only valid in the limit where v / v 1 which is satisfied when b = 2Gm / v v b_min where b_min Gm / v². Now integrating equation 7 over all possible impact parameters, b_min to R yields

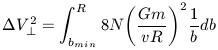
(19)

Defining R / b_min (the ratio of maximum to minimum impact parameters) then yields

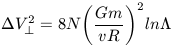
(20)

For a galaxy of equal mass stars we can define the orbital velocity of a star, at some radius R in the galaxy to be v² = GNm / R. Eliminating R from equation 20 then yields

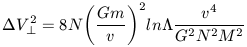
(21)

We are thus lead to the basic result

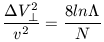
(22)

We operationally define a relaxation time as the amount of time it takes for v to be equal to v. That is, after enough encounters, the perturbations will be of the same amplitude as the initial velocity. According to equation 22, this will occur after a number of encounters given by N / (8 ln ), which we define as n_relax. The relaxation timescale is then just given by n_relax x t_cross where t_cross is the time it takes for the star to cross (orbit) the galaxy and is equivalent to a dynamical time scale (e.g., (G)^-1/2). Using the definition of = R / b_min and b_min Gm / V² then yields

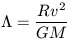
(23)

which is just N. So the relaxation time scale is

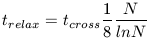
(24)

where t_cross is essentially R/V. Hence, although counter-intuitive, long range relaxation times slowly increase with increasing N.

If t_relax for some stellar system is larger than the age of the Universe then the system is said to be collisionless which means that stars move under the influence of the mean potential generated by all the other particles. For instance, a galaxy has N 10¹¹ and R/V 3 x 10⁸. This yields t_relax 10¹⁸ years which is 8 orders of magnitude older than the universe. A cluster of galaxies has N 10³ and R/V 10⁹. This yields t_relax 10¹¹ years and hence mass segregation should not be observed in clusters of galaxies.

A full derivation of the two-body relaxation time can be found in Binney and Tremaine (1987). Following that we can express the two-body relaxation timescale via the following parameterized equation:

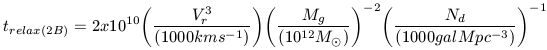
(25)

For a very massive galaxy, M_g ~ 10¹² M in a dense galaxy cluster (N_d ~ 1000 galaxies Mpc^-3) the two-body relaxation time scale is 20 billion years. These conditions describe a cluster like Coma. In dense clusters like Coma there is evidence that the most massive/brightest galaxies have settled to the bottom of the cluster potential (e.g., Beers and Geller 1983; Oegerle and Hill 1994). Alternatively, they could have merely formed in place at that location. Whether or not long range forces (equation 24) or two-body relaxation (equation 25) dominates probably depends upon the mass function of the galaxies in the cluster. A cluster with a few massive galaxies in it may have the shorter two-body relaxation timescale in which case those few massive galaxies will migrate to the center of the cluster potential and remain there. The essential point, however, is that relaxation times for clusters generally exceed the expansion age of the Universe

Collision Timescale: The collision timescale can be easily derived by treating a cluster of galaxies as being a thermodynamic state in a closed volume. In this volume there is number density of galaxies (N_d), a characteristic cross section ( R_gal²), and a characteristic velocity dispersion (V₃). The product, ((N_d) ( R_gal²) (V₃))^-1 defines a timescale which is the mean time between direct collisions of the particles. Dense systems with large galaxies and high velocity dispersions have shorter collision times. A convenient parameterization is:

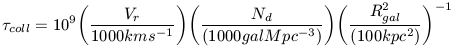
(26)

For a galaxy with R_gal ~ 10 kpc, the collision time scale in the dense core of the Coma cluster is, interestingly, comparable to the dynamical timescale! This suggests that galaxy evolution can be severely altered in such a dense environment.

Cooling Timescale: When cold gas from a galaxy in a cluster is liberated from the galaxy potential by some process, that gas heats up as it comes into virial equilibrium with the cluster potential. In the case where this gas is an ideal gas, the temperature of that gas is set up by the virial condition

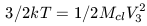
(27)

The observed values of M_cl and V₃ predict temperatures in the kev range and we expect most clusters to be filled with an X-ray emitting plasma. The cooling of that plasma is dominated by collisional processes with the hot electrons and the ions. This cooling is primarily done through metallic lines and therefore the heavy element abundance of the plasma is important. The cooling timescale depends upon the electron density n_e, the initial temperature, and the cooling coefficient appropriate for a particular gas composition. There is an order of magnitude difference in cooling coefficient for 0.1 solar metallicity gas and primordial (zero metallicity) gas (Silk and Wyse 1993). X-ray spectra of clusters, however, indicate that the ICM has a mean metallicity which is approximately solar. For this case, a convenient expression for the cooling timescale (see also Raymond et al. 1976) is

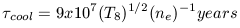
(28)

where T₈ is measured the temperature in units of 10⁸ K and n_e is measured in particles per cm^-3. Most clusters have n_e 10^-3 and hence when heated to a few T₈ K will remain so over a Hubble time.

Dynamical Friction Timescale: Dynamical friction is an odd astrophysical process and can only occur in specialized environments. It is caused when a smaller mass object passes nearby a larger mass object which itself is surrounded by a gravitationally bound halo of uniformly light particles. The typical situation is a large galaxy surrounded by a halo of 1 M stars. If the lower mass galaxy passes through this halo, that passage will create a gravitational wake which causes the low mass stars to line up behind the passing galaxy. This in turn exerts a small gravitational force on the smaller body causing it to lose some energy. Dynamical friction represents a kind of frictional drag which causes the lesser bodies motion to damp out. If the lesser body is on an orbit that makes repeated passages through that halo, its orbit will decay over time and it will spiral in and be acreted by the larger object, thus causing that larger object to grow in mass and size. During this process, tidal forces can act to strip more stars out of the lesser body building up the size of the halo.

Dynamical friction acts as a damping mechanism to remove orbital energy from cluster galaxies. Binney and Tremaine (1987) demonstrate that a galaxy of mass M_g which moves with velocity v experiences a deceleration due to dynamical friction given by

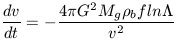
(29)

From this, we can make a straightforward derivation of the dynamical friction timescale to see if its a relevant process for clusters of galaxies. The characteristic timescale over which energy is lost via dynamical friction is defined as

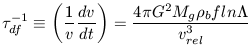
(30)

where f is a numerical value related to the distribution of the orbits in the potential, _b is the background density of light particles (e.g., 1 M stars), v_rel is the relative velocity of the companion galaxy, (not to be confused with the cosmological constant) is related to the impact parameter b_min as

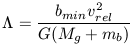
(31)

where m_b is the mass of the background particles.

For simplicity we assume circular orbits in which case f = 0.4 (see Binney and Tremaine 1987) and a flat rotation curve which satisfies the equation

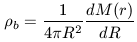
(32)

where M(r) follows from the virial theorem as

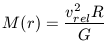
(33)

Substituting this into equation 30 yields

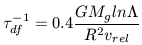
(34)

Recalling that _cross = R / V and parameterizing M_g by (M / L) L_g and making use of equation 33 leads to the general expression for the dynamical friction timescale

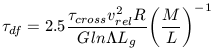
(35)

which expresses the friction timescale as some multiple of the dynamical timescale. In astrophysical units, equation 34 can be written as

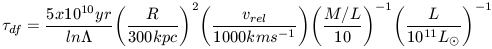
(36)

Cluster environments in which smaller galaxies have v_rel 300 km s^-1 and distances 200 kpc have values of _df t are less than H₀^-1. Hence, there are situations where dynamical friction could substantially alter the orbits of cluster galaxies and change the overall population of the cluster. But how prevalent is this?

In a study of central cluster environments, Bothun and Schombert (1990) suggest that 25% of all rich clusters are experiencing an augmentation to the luminosity/mass of the central dominant galaxy as dynamical friction causes the orbits of these central cluster galaxies to decay. Further support for this process comes from the observation that many galaxies in the central regions of clusters appear to have truncated surface brightness profiles. This is most likely due to the tidal liberation of stellar material during the close passage to the central dominant cluster galaxy. In order to prevent the entire depletion of this population over a Hubble time, it is necessary that the galaxies currently in the centers of these clusters are on relatively elongated orbits. For most galaxy clusters, dynamical friction is avoided if the orbits of the individual members are highly radial. Studies of other galaxy clusters by Gebhardt and Beers (1991) and Merrifield and Kent (1991) have reached similar conclusions.