


3.6. The Peculiar Velocity Field
Although redshift surveys have provided a wealth of data that has helped to discover and described LSS, this data is really one step removed from the more fundamental cosmological issue, namely, the distribution of mass. Redshift surveys probe the positions of galaxies in redshift space. This is not necessarily the same as physical space, as mass concentrations serve to distort the appearance of structure when its plotted in redshift space (see Kaiser 1986). A trivial example of this is provided by the fingers-of-god signature of virialized structures in redshift space. Recall that earlier in this chapter we briefly introduced evidence for significant amounts of non-luminous matter in clusters of galaxies. While the nature of the dark matter and its possible distribution is the subject of extensive discussion in Chapter 4, we have introduced here because it definitely effects the relation between redshift space and physical space. In fact, since we don't actually know what the mass distribution is, its total effect on the appearance of structure in redshift space is very difficult to ascertain.
In the previous discussion in which various correlation length scales were presented, it was implicitly assumed that the distribution of light is a fair and unbiased tracer of the distribution of mass. Under this assumption, voids (i.e., lightless areas) are also massless areas. The highly clustered nature of the light distribution would then be reflective of a highly clustered mass distribution. On the other hand, if the distribution of mass were smoother than the distribution of light (its hard to imagine under any circumstances that the mass distribution would actually be clumpier) then bias will be introduced if you assume that light traces mass. The simplest form of biasing assumes a linear relation between the galaxy density and the dark matter density:
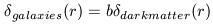
|
where b is the linear biasing factor. Expressed in this sense, b represents a large scale mean biasing value. Larger or smaller values on smaller scales can certainly exist (and probably do).
In chapter 5 we will discuss the physical basis for biasing. Here we treat it phenomenologically. Qualitatively, the issue of biasing stems from our lack of knowledge about the nature of dark matter and the structure formation process itself. Given this, it is clearly bold but dangerous to assume that most of this mass is actually trapped into some gravitational potential which also hosts a luminous galaxy. If this indeed were the case, then structure formation is very efficient as all of the mass would be contained in discrete potentials and there is little possibility for a smoother distribution of mass between these potentials. It seems unlikely that the structure formation process was this efficient and hence there is some expectation that the mass distribution should be smoother than the light distribution. In the extreme case where the mass distribution is smooth on the same scale as the galaxy distribution is clumpy, then there is a clear bias between the mass and light distributions.
Unfortunately, redshift surveys alone provide inadequate constraints on the relative distributions of dark and light matter. This is because any peculiar velocity introduced by the presence of a mass concentration will cause a distortion in redshift space along the line of sight. The effect is similar to the previously discussed case of a virialized structure in the case where the internal velocity dispersion is larger than the expansion velocity over the scale of the structure. In this case, the apparent separation pairs of galaxies will appear much larger in redshift space than it is in physical space. In the situation where there is a mean infall of some group of galaxies towards a larger mass concentration (such as the infall of the Local Group to Virgo), then some compression in redshift space relative to physical space will occur as the Hubble expansion velocity has been retarded by this gravitationally generated infall. Thus distortions in redshift space can provide clues to locations which have significant peculiar velocities but any further progress relies on measuring the relative distances of galaxies in order to derive the amplitude of the peculiar velocity.
We define a peculiar velocity as difference (positive or negative) between the predicted expansion velocity of a galaxy and its observed velocity. Thus, we can only measure peculiar velocities in the radial direction. The determination of peculiar velocities involves only relative distances and hence is independent of the actual value of H0. Peculiar velocities are determined via the following steps:
1. Choose a reference frame, which is at rest with respect to the CMB (which is assumed to be an inertial frame). This reference frame could either be the observed velocity transformed to the CMB frame, or a relative velocity with respect to some structure that is at rest with respect to this frame. The Coma cluster is generally chosen for this latter purpose.
2. Using some distance measuring technique, determine the relative distance of a galaxy from the Coma cluster.
3. Use the relative distance to predict the observed velocity. For example, the CMB frame velocity of Coma is about 7200 km/s. If we measure some galaxy to have a relative distance modulus to Coma of (m - M) = +0.75 (e.g., a factor of 2 in distance) then its predicted observed velocity would be 7200 x 2 = 14,400 km s-1.
4. Compare the predicted velocity with the observed velocity. A non-zero difference (outside of the measurement errors) represents a peculiar velocity. In the example just cited, if the observed velocity (again in the CMB frame) is 16,000 km/s, then
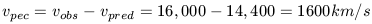
|
The physical meaning of this peculiar velocity is that this galaxy has a +1600 km/s departure from its expansion motion with respect to us. Such a departure could be generated by the infall of this galaxy to a more distant virialized structure. The 600 km/sec motion of the Milky Way galaxy, as measured by the observed CBR Dipole Anisotropy is an example of such an induced motion (see more below).
An understanding of error propagation in this methodology is vital
to assessing the quality and credibility of derived peculiar velocities.
This is treated in great detail by Strauss and Willick (1995).
The main problem is that relative galaxy distances must
be determined to fairly high accuracy. Since this is difficult to
achieve with any galaxy sample, the subsequent determination
of the peculiar velocity field is rather imprecise because
the data are inherently noisy. Errors in the peculiar velocity
are directly proportional to fractional errors in the distance
determination. If you are able to measure the relative distance
of a galaxy to an accuracy of 10% (which is good), then that
translates into a 1 error of
500 km/s at a mean redshift
of 5,000 km/s. At a minimum, a secure measurement requires S/N of
at last 3
error of
500 km/s at a mean redshift
of 5,000 km/s. At a minimum, a secure measurement requires S/N of
at last 3 which translates into
1500 km/s, or a 30%
deviation from Hubble expansion velocity. Although the size of this
error bar can be reduced by N1/2 if one uses a sample
of galaxies
all in one cluster, our overall ability to measure small (i.e.,
which translates into
1500 km/s, or a 30%
deviation from Hubble expansion velocity. Although the size of this
error bar can be reduced by N1/2 if one uses a sample
of galaxies
all in one cluster, our overall ability to measure small (i.e.,
 10%) deviations from Hubble flow is limited.
This difficulty can give
the illusion (see Tammann and Sandage 1995) that the local
Hubble expansion is quite smooth. For instance, at 20,000 km/s
some galaxy might have a 1,000 km/s perturbation due to its proximity
to a mass concentration but when viewed from earth, that galaxy
will be close to the Hubble line. This is schematically shown in
Figure 3-15.
10%) deviations from Hubble flow is limited.
This difficulty can give
the illusion (see Tammann and Sandage 1995) that the local
Hubble expansion is quite smooth. For instance, at 20,000 km/s
some galaxy might have a 1,000 km/s perturbation due to its proximity
to a mass concentration but when viewed from earth, that galaxy
will be close to the Hubble line. This is schematically shown in
Figure 3-15.