4.1.1. The Virial Theorem

Because the virial theorem is of central importance in dynamical mass estimates it is worthwhile to derive it in a rigorous manner using the moment of Inertia of a system of N-particles. For this system, we define the moment of inertia I as

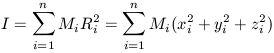
(1)

After one dynamical timescale, the time derivative of I is constant so the second derivative is zero. Hence we can write

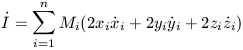
	(2)
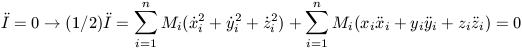
	(3)

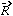
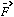The first term on the right hand side is _i=1ⁿ M_iV_i² which is twice the kinetic energy of the system or 2T. The second term consists of a spatial coordinate times its second derivative which is displacement times force which is an energy. We identify the second term as _i=1ⁿ where 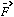is the total Force. This term is the potential energy of the system or W. We thus have

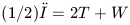
	(4)
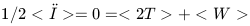
	(5)

which is the well known virial theorem in which the total energy of a system is zero.

For a self-gravitating N-body system

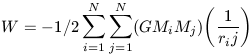
(6a)

If we assume that each particle as the same mass then M_i = M_j + M_t / N where M_t = total system mass. This yields

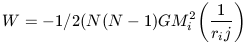
(6b)

For large N, this reduces to

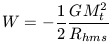
(6c)

where R_hms is the harmonic mean separation between the system of N particles. The kinetic energy of this system is

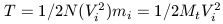
(6d)

The time average of V_i is defined to be the r.m.s velocity dispersion of the system, _v. By the virial theorem we then have

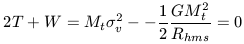
(6e)

or

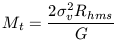
(6f)

which indicates that under the virial theorem, masses can be derived by measuring characteristic velocities over some characteristic scale size. In general, the virial theorem can be applied to any gravitating system after one dynamical timescale has elapsed.