4.3.3. Stellar Population Effects

The data discussed above has resulted in a large range of estimated M / L values for individual galaxies. Before discussing that, it is worthwhile to understand the range of M / L values that can arise solely from differences in stellar populations. The mass distribution of stars that arises from star formation is reasonably well-fit by a power law over the mass range M_u and M_l where the u and l refer to upper and lower mass limits. A parameterization of this power law is

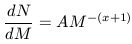
(18)

where A is a normalization function, The sense of this relation is that larger values of x produce preferentially more low mass stars. The M / L value for a stellar population depends upon both x and M_l. In fact, the dependence on M_l is most critical. The sense of any power law distribution is to make a few big things and a lot of little things. The minimum mass required for sufficient core temperature to initiate nuclear reactions is 0.07 M. If equation 18 holds down to M_l = 0.01 M, then a great deal of sub stellar mass objects can be produced in a star formation event and a significant fraction of the total mass which is formed will be stored in an essentially unobservable form. These sub stellar mass objects are known as "brown dwarfs". Hence, knowledge of the faint end slope of the stellar luminosity function is directly relevant to the problem of dark matter in galaxies.

Detailed studies of faint star counts by Neil Reid and colleagues give credible evidence that a single value of x is not an appropriate description of the mass function once the mass gets below 0.3 M. The data indicate that the mass function tends to flatten out and moreover, despite intensive observational searches, there is no evidence that objects of 0.01 M exist in significant numbers, In fact, there have only been 2 good brown dwarf candidates discovered to date (see Kulkarini et al. 1995). Interestingly, the recent discovery of planets around nearby stars by Geoff Marcy and his collaborators (see Marcy and Butler 1997) have indicated that 0.001 M objects are common. Hence, their appears to be a real astrophysical gap between 0.001 M and 0.07 M.

A description of how x is determined would fill more pages than our entire cosmology book. Suffice it to say that values of 1-1.5 are consistent with the data. But there may be a circular argument involved in this determination. A value of x in the range 1-1.5 will populate the mass range 1-2 M. These stars have lifetimes of 10⁹ - 10¹⁰ years and will dominate the light of a galaxy when they are either A main sequence stars or Red Giants. Since the lifetime of Red Giants and A main sequence stars is only about 10% of the total stellar age of the galaxy, then at any epoch these galaxies will have their light dominated by only a small percentage of the total stars. Moreover, as the aggregate brightness of thousands of Red Giants is large, the galaxy itself will be fairly luminous and easily detectable. Determinations of x repeatedly are based on samples of easily detectable galaxies thus recovering the range of 1-1.5. Since we don't understand the physics that produces x and M_l it is worthwhile to consider two alternative star formation scenarios that would produce "dark" galaxies:

The low mass star dominated galaxy: The percentage of mass that forms in stars with masses lower than 1 M is strongly dependent on x. For x in the range 1-1.5 this percentage varies between 40 and 70%. In the case where x is as steep as 2.5, the percentage climbs to 95%. In this case, most all of the stellar mass is in a form where the main sequence lifetime exceeds H₀^-1 and such a galaxy will have few, if any, Red Giant stars. In this case, at fixed mass, when observed at the current epoch, the galaxy would have 10³ - 10⁴ times less luminosity, depending upon what M_l is and if the power law can really be extended all the way down to that mass. Such a galaxy would therefore be very red, very diffuse have a very high M / L and be almost impossible to detect (see Chapter 6). Since this galaxy never had any massive stars, it would also be quite deficient in heavy elements.

The remnant dominated galaxy: The opposite case is one where x 0 and/or M_l is 1 M. In this case, star formation places most of the mass in stars with masses greater than 2 M. These are very bright initially, but don't live very long. Furthermore, the energy feed back from the massive stars and their subsequent supernova phases of evolution may well be sufficient to drive the remaining gas completely out of the galaxy. This would be a case of terminal star formation in that the star formation event was so vigorous that the remaining cold gas has been heated (perhaps to escape velocity) thus preventing further star formation. The lack of a substantial reservoir of low mass stars in this scenario means that the galaxy has a luminous phase which only lasts about 10% of a Hubble time. After that phase has ended, the galaxy is destined to fade rapidly and end up as an extremely diffuse, perhaps somewhat blue, with very high M / L as it would be dominated by stellar remnants (e.g., white dwarfs, neutron stars and black holes). As discussed in Chapter 6, there is evidence from deep galaxy counts and redshift surveys for a population of blue galaxies at intermediate redshift they may have faded to become a "dark" galaxy at z = 0.