5.1.1. The Continuity Equation

We define a small volume element, v which is fixed in space in an assumed non-relativistic fluid. Motion within the fluid will cause material to flow in and out of this fixed volume element which will cause its density to fluctuate with time. For simplicity we assume the fluid flow to be in the direction x. These density fluctuations are directly correlated with the rate of fluid flow through the volume element. The mass flow is v. Since the total mass within the fluid is assumed to be a constant then the divergence of the outward mass flow across the boundaries of the fixed volume element must be equal to the rate of decrease of the density within the volume element. This specifies the condition for the equation of continuity:

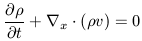
(1)