


5.1.4. Gravitational Instability in an Expanding Universe
The expanding medium means that for any small density perturbation, there will be competition between its self-gravity which is attempting to increase the density, and the general expansion of the universe which decreases the density. Initially, the expansion rate of the Universe was very high which makes it difficult for any perturbation to grow by continually increasing its density. Nevertheless, if we restrict ourselves to a specific physical regime, we can apply the previous formalism to problem of perturbation growth in an expanding medium. To do this, we make three assumptions:
 we only consider
perturbations on scales smaller than the
horizon size (recall that the COBE measured anisotropy is for many
horizons)
we only consider
perturbations on scales smaller than the
horizon size (recall that the COBE measured anisotropy is for many
horizons)
 we assume non-relativistic
perturbations only
we assume non-relativistic
perturbations only
 we assume that pressure is
negligible; on the scale of the
horizon, this assumption is justified after inflation ends.
we assume that pressure is
negligible; on the scale of the
horizon, this assumption is justified after inflation ends.
In the previous treatment in a static medium, we were allowed to set v0 = 0. But since the medium is now expanding, its initial velocity clearly can't be zero. However, we can still retain the simplifying assumptions of homogeneity and isotropy in the fluid. That is,
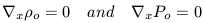
|
We then proceed as before but retain all terms which have v0 and we start with
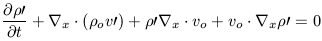
| (22a) |
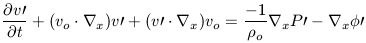
| (22b) |
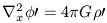
| (22c) |
with only Poisson's equation being, of course, unchanged.
Recall that the Eulerian approach examined the behavior of a fixed point in space. In an expanding universe, the density at this fixed point will change with time both due to the expansion of the Universe and the real growth of perturbations due to gravitational instability. If we transform the fluid dynamic equations to a reference frame that follows the general expansion, these two effects can be separated. Transforming to this frame means converting from the Eulerian approach to the Lagrangian description. The relationship between the Lagrangian and Eulerian derivatives can be expressed as
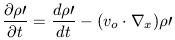
|
Substituting this into the equation of continuity and using the
vector identity  x
.
x
.
 v =
v =

 x . v +
v .
x . v +
v .  x
x
 yields
yields
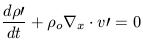
| (23) |
or
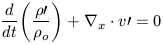
| (24) |
We now define the density contrast
 to be the dimensionless quantity
to be the dimensionless quantity
 ' /
' /
 which leads to
which leads to
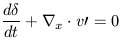
| (25) |
This is the Lagrangian form for the equation of continuity. Implicit in this form is the use of an absolute coordinate system. We now make use of a coordinate transformation that will define a system of coordinates that are comoving with the universal expansion. The advantage of describing the behavior of the fluid in comoving coordinates is that for a fluid element moving with the overall expansion, its comoving position, r, remains constant. Its physical coordinate (x, of course, would be constantly changing. The comoving position, r, can be expressed as
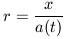
|
where a(t) is the time evolution of the universal scale factor, a, first presented in Chapter 1 as R(t). Thus
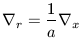
| (26) |
where  r refers to
derivatives that are done with respect to
comoving coordinates. In addition to a spatial coordinate transformation,
we also want to transform the absolute velocity of a fluid element which
is located at fixed spatial position, x. The motion of this fluid will
have two components, one driven by the general expansion of the Universe,
and the other is a peculiar velocity that can arise as a result of some
external perturbation.
We transform the proper velocity v(r, t) via the following
r refers to
derivatives that are done with respect to
comoving coordinates. In addition to a spatial coordinate transformation,
we also want to transform the absolute velocity of a fluid element which
is located at fixed spatial position, x. The motion of this fluid will
have two components, one driven by the general expansion of the Universe,
and the other is a peculiar velocity that can arise as a result of some
external perturbation.
We transform the proper velocity v(r, t) via the following
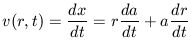
|
where the first term represents the normal expansion of the fluid due to the expansion of the universe (this term is equivalent to v0 in the previous treatment) and the second term is the peculiar velocity. In the context of linear perturbation theory, this peculiar velocity, if small, can be associated with what we have been calling v'. It is convenient to further express the comoving perturbed velocity dr / dt as u such that it satisfies
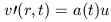
|
We can now specify the comoving form of the 3 basic fluid equations. In Lagrangian form they are
Equation of continuity:
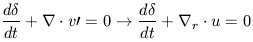
| (26a) |
Perturbed Euler Equation:
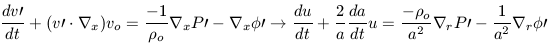
| (26b) |
Perturbed Poisson Equation:
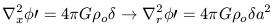
| (26c) |
Recall that our main objective is to determine the rate of growth of
density perturbations,  , in
this expanding medium. We proceed
as before by first taking the time derivative of the equation of
continuity, now expressed in comoving form.
, in
this expanding medium. We proceed
as before by first taking the time derivative of the equation of
continuity, now expressed in comoving form.
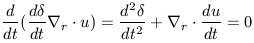
| (27) |
Next we take the divergence of Euler's equation
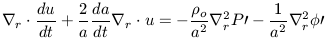
| (28) |
Using the previous expressions we can now eliminate terms involving
u as they have been rewritten to terms involving
 , the
physical quantity of interest. Finally, by making use of Poisson's
equation we can derive
, the
physical quantity of interest. Finally, by making use of Poisson's
equation we can derive
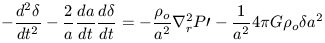
| (29) |
and using the relation cs2 = dp /
d =
P' /
=
P' /
 ' we can derive
' we can derive
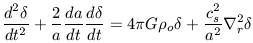
| (30) |
We have now arrived at our full specification of the time evolution of
density perturbations in an expanding universe. We can compare this
"wave" equation with equation 17, the case for the static medium to
discern the presence of the additional term involving da / dt
(or  ). This term, which must be
positive in an expanding
Universe, clearly shows that universal expansion acts to retard the
growth rate of density fluctuations. Furthermore, as in the static
medium case, we still have the same competition between pressure and
gravity. Hence the Jeans length criteria remains valid and in
this formulation can be thought of as a competition between two timescales,
the characteristic timescale for gravitational growth,
(G
). This term, which must be
positive in an expanding
Universe, clearly shows that universal expansion acts to retard the
growth rate of density fluctuations. Furthermore, as in the static
medium case, we still have the same competition between pressure and
gravity. Hence the Jeans length criteria remains valid and in
this formulation can be thought of as a competition between two timescales,
the characteristic timescale for gravitational growth,
(G
 0)-1/2
and the crossing time,
0)-1/2
and the crossing time,
 j /
cs for a pressure wave to move
across the Jeans length scale. For wavelengths much longer than the
Jeans length, this crossing time will be very much longer than the
gravitational free fall time and the solutions to equation 30 are
pressureless. In this case we solve
j /
cs for a pressure wave to move
across the Jeans length scale. For wavelengths much longer than the
Jeans length, this crossing time will be very much longer than the
gravitational free fall time and the solutions to equation 30 are
pressureless. In this case we solve
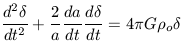
| (31) |
in two important limiting cases,
 = 1 and
= 1 and
 << 1.
<< 1.