5.1.6. The << 1 case

Here the simplest thing to do is to assume = = 0. For this case,

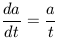
and our wave equation reduces easily to

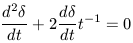
Using our power law t trial solution we can write

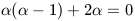
which has the two solutions = -1 (similar to before) and = 0. Thus in an empty universe, or more realistically, in a very open universe, there is no time dependence on the growth of fluctuations. Instead, they maintain themselves at a constant comoving density. This is because there is simply very little matter to generate any self-gravity. structure. The matter density is a function of the redshift at which it is measured. Specifically, for Friedmann models

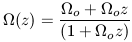
where ₀ is the present value. From the observations previously discussed, ₀ appears to be in the range 0.1-0.3. In this case, at z = 10, was at least 0.55 and at z = 100 it would be nearly 1. In fact, (z) is only independent of redshift in the special cases of = 0 or 1. In the former case, the Universe has always been massless and none of us are here, whereas the latter case is predicted from inflation. The important point is that, even in a low density Universe, the major time of perturbation growth from z = 1100 to z = 10 would have occurred in the domain of 1 in which case the growth rate goes as t^2/3. Note that in an open universe, there will be some redshift at which does begin to significantly deviate from 1 leading to a much slower growth rate. Hence, structure formation in an open Universe effectively is over when (z) approaches 0. This condition is satisfied by z (1 / ₀) - 1. Thus if ₀ is 0.1 then structure formation by this process should be over at redshift z = 9.