5.2. Statistical Characterization of Structure

Structure as a function of physical scale size (wave number) is usually described in terms of a power spectrum:

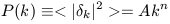
(32)

where _k is the Fourier transform of the primeval density fluctuations which are amplified by gravity to produce the observed structure. These density fluctuations give rise to the observed CMB anisotropy and thus _k has some observational constraint. The spectral index, n determines the relative distribution of power on various scales. Values of n which are less than 0 produce a spectrum with power on very large scales. The amplitude, A, is dependent upon which structure formation scenario is being considered. In principle, A is also subject to observational constraint. P(k) itself is most correctly considered as the functional representation of the power per unit volume in k-space (see Bertschinger 1992). Observations reveal the power (or correlation function) per unit volume in physical space. It is then necessary to define a framework that allows these observations to be mapped back on to P(k). This greatly restricts the choices of structure formation scenarios which can be observationally constrained (see Strauss and Willick 1995). As discussed in more detail below, this mapping can only be done under the hypothesis that the phases of _k are random. Fortunately, the random-phase hypothesis is directly predicted from inflation and in fact, would hold in any Universe which is isotropic (i.e., there is no preferred direction).

The determination of P(k) only provides a statistical description of the observed distribution of density fluctuations. By itself, it provides little physical information for the actual formation of structure but instead statistically characterizes the range and frequency of scales over which structure does form. For instance, it is possible (and in some cases easy) to construct a physical scenario that predicts a form for P(k) that roughly agrees with observations, but which contains no real physics to produce structure itself. Hence one needs to be wary and carefully differentiate between statistical structure formation models and physical ones (one of course wants a model which can do both).

This need to differentiate is quite clear when one considers structure formation via gravitational instability. The amplification of initial density fluctuations on some scale _r, naturally produces a statistical density field. In turn, this statistical density field produces a statistical distribution of structure collapse and formation times. As structures on different scales collapse at different times, there well may be energy feedback to the entire system which interferes with the collapse of lower density structures. This feedback is not accounted for by any statistical theory. A possible example is provided by QSOs. Suppose QSOs are the collapse of sub-galaxy scale very dense perturbations. A massive star cluster forms out of the gas initially (perhaps being the first generation of stars to produce metals). The subsequent evolution of the massive star remnants into black holes and neutron stars gravitationally coalescence to form a super massive black hole. As baryonic gas continues to infall on this dense seed, it becomes the power source for the QSO and suddenly the Universe contains a large number of sources of ionizing radiation. If this occurs while other collections of neutral hydrogen gas inside dark matter potentials are quiescently collapsing, then it will be a significant source of reheating and will further delay the formation of these systems. One could even conceive of situations where the energy feedback from material falling on these dense structures might evacuate regions around them leading to the formation of a void.

Thus, in fairness, it is really is quite unclear if the apparent cellular pattern in the galaxy distribution which is manifest in the distribution of voids, walls and clusters can actually be physically produced from gravitational instability alone. Indeed, the overall local topology strongly implies that structure formation has a hydrodynamic component associated with it and it is quite difficult to fold this into efforts to recover both P(k) and real galaxy formation. Structures like the Great Wall are extremely difficult to understand from gravitational instability considerations alone as its likely the Universe is not old enough to have built such a large structure in this manner. Thus the profound theoretical challenge which is posed by the complexity of the observed galaxy distribution lies in achieving a physical understanding of the processes than can produce a void filled universe, with small scale structure apparently forming at the intersections between these voids.

Adding to this complex mix is our unfortunate situation regarding the unknown makeup and amount of dark matter in the Universe. Structure formation scenarios are almost totally driven by the assumed form of dark matter as well as its overall contribution to the mass density of the Universe. Each form of dark matter carries with it different predictions of the form of P(k). In the simplest terms, CDM scenarios involve non-relativistic particles that dissipate and clump at very early times to form small scale structure. HDM involves relativistic particles that can not clump early on but instead can generate only large scale perturbations and thus power on large scales.