6.3. Surface Brightness Selection Effects

Within the idealized framework of azimuthally symmetric galaxy profiles, the luminosity profile of a disk galaxies is given by

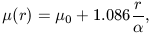
(10)

where µ₀ is the central surface brightness of the disk and is its angular scale length which corresponds to the physical scale length _l at distance d. These two parameters characterize the light distribution of the idealized disk galaxy, and together determine the integrated luminosity,

(11)

Here ₀ is the central surface brightness in linear units, and

gives the fraction of the light contained within a finite number of scale lengths x,

(12)

relative to that contained in an exponential profile extrapolated to infinity (Disney & Phillipps 1983, hereafter DP). These simple formulas provide adequate fits to most spiral galaxies (de Vaucoulers 1959), and in particular to low surface brightness (LSB) galaxies (McGaugh and Bothun 1994; de Blok, van der Hulst, & Bothun 1995).

Freeman (1970) found that all spiral disks have essentially the same central surface brightness, µ₀ = (21.65 ± 0.3) B mag arcsec^-2 This has become known as ``Freeman's Law.'' If correct, the number of parameters relevant to galaxy selection reduces to one as only variations in size modulate those in luminosity. Since µ₀ is a measure of the characteristic surface mass density of a disk, Freeman's Law requires that all the physical processes of galaxy formation and evolution conspire to result in this very specific value for all galaxies. Either the surface mass density must be the same for all galaxies (in itself a peculiar result) with little variation in the mass to light ratio, or variations in the star formation history, collapse epoch and initial angular momentum content must all conspire to balance at this arbitrary value. It is thus important to rigorously test the reality of Freeman's Law as the distribution of µ₀ may be directly related to the conditions of galaxy formation (Freeman 1970; McGaugh 1992; Mo, McGaugh, & Bothun 1994).

The Freeman value is about 1 magnitude brighter than the surface brightness of the darkest night sky. That the number of galaxies with faint central surface brightnesses appears to decline rapidly as µ₀ -> µ_sky is suspicious and if true of the real galaxy population implies that our observational viewpoint is privileged in that we are capable of detecting most of the galaxies that exist, at least when the moon is down. This again is the essence of the argument voiced by Disney (1976) in characterizing the Freeman Law as a selection effect. To assess the validity of these arguments, it is necessary to construct a "visibility" function which basically determines the volume sampled by galaxy surveys as a function of central surface brightness. Existing galaxy catalogs are the result of this visibility function convolved with the intrinsic bivariate galaxy distribution (M, µ₀). Here, we the derive visibility as a function of the two disk parameters µ₀ and _l by considering galaxy selection based on either isophotal diameter limits of magnitude limits.