6.3.2. Flux-limited Catalogs

For flux limited samples where isophotal magnitudes are employed, the selection parameters are the magnitude limit m_l and the isophotal limit µ_l above which the flux is measured. Samples limited by total flux do not exist, since survey material always has an effective isophotal limit below which very diffuse galaxies can not be identified, regardless of their total flux. Such galaxies do exist (e.g., Malin 1 and its cousins; Bothun et al. 1987; Impey & Bothun 1989); Malin 2 (Bothun et al. 1990) has an apparent magnitude of B = 14.2 but is contained in neither the NGC, which contains many fainter galaxies, nor the UGC (Nilson 1973), which in addition to the limit _l = 1' is also supposedly complete to the usually less demanding limit B_l = 14.5.

For magnitude limited samples, DP (again, see their equation 31) find

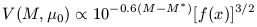
(17)

(f(x) is equivalent to their L_ap / L_T), which is plotted in Fig 6-7. V L^3/2, can be decomposed into ₀ and _l using equation (11):

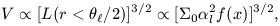
(17a)

so

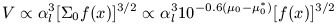
(18)

The latter form is shown in Fig 6-8.

The essential feature to note is that flux selected samples will have apparent distributions of µ₀ even more strongly peaked around the brightest extant value µ₀* than diameter limited samples, because the factor 10^{-0.6(µ₀-µ₀*)} varies more rapidly than does (µ₀ - µ₀*)³. At any given (plausible) value of µ_l, magnitude limited samples will detect more galaxies in total than diameter limited ones. However, they will be strongly dominated by _l*, µ₀* (and hence L*) galaxies. Diameter selection yields samples which are less strongly biased and hence more representative of the general field population. This is clearly seen in that there are a significant number of LSB galaxies contained in the UGC (McGaugh & Bothun 1994; de Blok et al. 1995) and virtually none in the pseudo-flux selected Zwicky catalog (see Bothun and Cornell 1990).

In either case, the volume over which LSB galaxies can be detected is very small. It goes to zero if the central surface brightness happens to be fainter than the selection isophote, even if the galaxy in question is intrinsically luminous. Examples of luminous galaxies with such faint central surface brightnesses are now known to exist. Proper selection of galaxies requires a two dimensional description of the completeness limit of a survey, not just a magnitude limit. At the end of this discussion we will use these volume corrections, in conjunction with surveys for LSB galaxies, to show that the Freeman Law is an abysmal representation of the surface brightness distribution of disk galaxies and that at least 1/2 of the general galaxy population has been missed to date. Twenty years after Disney's conjecture, this is the major quantitative result that confirms this early widsom.