


6.4.1. The Space Density of Galaxies as a Function of µ0
With the results of these new surveys in hand, we can use our surface
brightness selection formulism to make a preliminary estimate of the
space density of galaxies as a function of surface brightness.
To determine this, a correction for volume sampling effects
must therefore be applied to the survey data (see McGaugh et al. 1995 for
more details). Ideally, we should determine the bivariate galaxy distribution
 (
( l, µ0)
from complete catalogs for which the selection parameters
µl
and
l, µ0)
from complete catalogs for which the selection parameters
µl
and  l or
ml are carefully specified and rigorously applied.
Large catalogs which obey these strict criteria do not yet exist.
Another requirement for the measurement of the bivariate distribution
is that surface photometry be performed on all objects (i.e.,
µ0 and
l or
ml are carefully specified and rigorously applied.
Large catalogs which obey these strict criteria do not yet exist.
Another requirement for the measurement of the bivariate distribution
is that surface photometry be performed on all objects (i.e.,
µ0 and
 l
must actually be measured). This has not often been done, and
satisfying these criteria is really the best reason for performing a
uniform digital sky survey for galaxy selection. It is therefore
anticipated that the Sloan Digital Sky Survey (see
chapter 7)
will confirm much of what we present below.
l
must actually be measured). This has not often been done, and
satisfying these criteria is really the best reason for performing a
uniform digital sky survey for galaxy selection. It is therefore
anticipated that the Sloan Digital Sky Survey (see
chapter 7)
will confirm much of what we present below.
A final requirement for measuring
 (
( l, µ0) is that redshifts be
measured in order to extract absolute information (i.e.,
l, µ0) is that redshifts be
measured in order to extract absolute information (i.e.,
 l instead of
l instead of
 ).
No samples exist which meet all these requirements, though some come
close (de Jong & van der Kruit 1994). Phillipps et al. (1987) and
Davies (1990) do present data which meet the requirements for rigorous
selection and measurement of µ0, lacking only
redshifts. These data sets consist of complete samples of several hundred
galaxies selected by isophotal
magnitude (in the case of Phillipps et al. 1987) and both isophotal
magnitude and
diameter in the case of Davies (1990). The survey of Phillipps et al. (1987)
is in the field of Fornax, but all higher surface brightness galaxies
(those with µ0 < 23) are
expected to be in the background field (Ferguson 1989; Irwin et al. 1990).
Davies (1990) surveyed both Fornax and the adjacent field; we are concerned
only with the field data. The isophotal level of selection of Phillipps
et al. (1987) is µl = 25.5 mag
arcsec-2 and that of the Davies (1990) field
data is µl = 25.3, both in the
BJ band.
The relevant input data here are the number of galaxies
detected at each central surface brightness,
N(µ0) (i.e., the apparent distribution).
).
No samples exist which meet all these requirements, though some come
close (de Jong & van der Kruit 1994). Phillipps et al. (1987) and
Davies (1990) do present data which meet the requirements for rigorous
selection and measurement of µ0, lacking only
redshifts. These data sets consist of complete samples of several hundred
galaxies selected by isophotal
magnitude (in the case of Phillipps et al. 1987) and both isophotal
magnitude and
diameter in the case of Davies (1990). The survey of Phillipps et al. (1987)
is in the field of Fornax, but all higher surface brightness galaxies
(those with µ0 < 23) are
expected to be in the background field (Ferguson 1989; Irwin et al. 1990).
Davies (1990) surveyed both Fornax and the adjacent field; we are concerned
only with the field data. The isophotal level of selection of Phillipps
et al. (1987) is µl = 25.5 mag
arcsec-2 and that of the Davies (1990) field
data is µl = 25.3, both in the
BJ band.
The relevant input data here are the number of galaxies
detected at each central surface brightness,
N(µ0) (i.e., the apparent distribution).
The most crucial data set in this investigation
is provided by Schombert et al. (1992).
This catalog does not measure µ0 for all galaxies
in complete samples
in the sense described here, but it does contain a large number of
(~ 200) of LSB galaxies with

 1' measured at
µl
1' measured at
µl
 26 B mag
arcsec-2. This catalog is
characterized by disk galaxies of typical
(
26 B mag
arcsec-2. This catalog is
characterized by disk galaxies of typical
( l*) size but low
surface brightness, having a distribution very sharply peaked at
µ0 = 23.4 (McGaugh & Bothun 1994; de Blok et al. 1995).
Since surface brightness is distance independent, we do not need redshifts
to derive the surface brightness projection of the bivariate distribution.
The relative number density of disk galaxies as a function of central
surface brightness,
l*) size but low
surface brightness, having a distribution very sharply peaked at
µ0 = 23.4 (McGaugh & Bothun 1994; de Blok et al. 1995).
Since surface brightness is distance independent, we do not need redshifts
to derive the surface brightness projection of the bivariate distribution.
The relative number density of disk galaxies as a function of central
surface brightness,
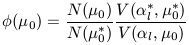
| (19) |
follows from the apparent distribution corrected for volume sampling.
The surface brightness distribution follows directly from the observations
(N(µ0) an µl)
and equation 19 given one assumption. The volume correction factor
depends on distance dependent (scale length in physical units -
 l)
as well as independent quantities
(µ0), so it is necessary to make an assumption
about
l)
as well as independent quantities
(µ0), so it is necessary to make an assumption
about
 l. As before
we assume
l. As before
we assume  l is
independent of µ0.
Thus, at any µ0, the effects of volume sampling
due to variations
in
l is
independent of µ0.
Thus, at any µ0, the effects of volume sampling
due to variations
in  l on average
cancel out, and only those due directly to µ0
matter. Hence we make the approximation
l on average
cancel out, and only those due directly to µ0
matter. Hence we make the approximation
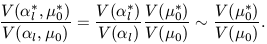
|
Our assumption that scale length is uncorrelated
with µ0 is borne out by a wealth of observational data
(Romanishin, Strom & Strom 1983; Davies et al. 1988;
Irwin et al. 1990; McGaugh & Bothun 1994; de Blok et al.
1995; McGaugh, Schombert, & Bothun 1995). Even
if this assumption were incorrect, it does not alter the basic conclusion
that there must be a relatively large space density of LSB galaxies,
simply because V-1 ->
 as µ0
-> µl.
The detection of any galaxy with a central surface brightness within
a few magnitudes of the selection isophote immediately implies a large
density of such objects.
as µ0
-> µl.
The detection of any galaxy with a central surface brightness within
a few magnitudes of the selection isophote immediately implies a large
density of such objects.
The surface brightness distribution determined from our assumption that
 l and
µ0 are uncorrelated
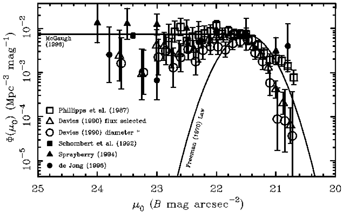
is shown in Figure 6-12. The data have a
long, approximately flat tail towards
lower surface brightness. That is, approximately equal numbers of disk
galaxies exist at each central surface brightness (as suspected by
Disney 1976). This is only true faintwards of the Freeman value,
which we have chosen as the fiducial
µ0*. Brighter than this, there
is an exponential cutoff. Though the extant data are not in perfect
agreement as to how steep this cutoff is, there is a clear turndown.
The major revelation of Figure 6-12 is clear
and far reaching:
diffuse galaxies do exist and they exist in substantial numbers;
they are just harder to see.
l and
µ0 are uncorrelated
is shown in Figure 6-12. The data have a
long, approximately flat tail towards
lower surface brightness. That is, approximately equal numbers of disk
galaxies exist at each central surface brightness (as suspected by
Disney 1976). This is only true faintwards of the Freeman value,
which we have chosen as the fiducial
µ0*. Brighter than this, there
is an exponential cutoff. Though the extant data are not in perfect
agreement as to how steep this cutoff is, there is a clear turndown.
The major revelation of Figure 6-12 is clear
and far reaching:
diffuse galaxies do exist and they exist in substantial numbers;
they are just harder to see.
|
Figure 6-12: Space density as a function of central surface brightness resulting from the volumetric corrections discussed in this chapter. |
The Gaussian surface brightness distribution advocated by Freeman (1970) fails seriously to describe the true intrinsic distribution. It underestimates the number of galaxies with µ0* > 23 mag arcsec-2 by over five orders of magnitude. No adjustment to the assumption about the scale length distribution made here can reconcile the data with a Freeman Law. The monumental difference between what Freeman's Law predicts and what is actually observed is a strong testimony to the fact that a proper survey for galaxies has yet to be done and that much of the baryonic material tied up in disks is contained in a fairly diffuse, hard to detect population. This constancy of disk galaxy number density as a function of µ0 is the most significant result obtained to date on LSB galaxies and strongly alters the conventional view of the galaxy population, which suggests that they are at most a few percent of galaxies by number.
The basic point of Figure 6-12 is twofold: 1)
Clearly the large departure
of real data from Freemans law indicates that we do not yet have a
representative sample of galaxies at z = 0. Because of that, it is
very dangerous to use deep galaxy counts to proclaim there is some
excess in the space density of galaxies relative to that in the
nearby Universe; 2) Clearly a substantial population of galaxies
with low µ0 exist and they contain a significant
amount of baryonic material. A conservative estimate, based on
Figure 6-12, suggests
that at least 1/2 of the mass in disk galaxies is contained in
systems with µ0
 22.0 mag arcsec-2.
22.0 mag arcsec-2.