Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
499-542 Copyright © 1992 by Annual Reviews. All rights reserved |
3.1 Expansion Dynamics
If a  1/(1 + z)
1/(1 + z)
 R/R0 is the
expansion factor relative to the
present (z being the redshift), and if
R/R0 is the
expansion factor relative to the
present (z being the redshift), and if

 H0t
is a dimensionless time
variable (time in units of the measured Hubble time
1/H0), then
Equation 1 can be rewritten in terms of measurable quantities as
H0t
is a dimensionless time
variable (time in units of the measured Hubble time
1/H0), then
Equation 1 can be rewritten in terms of measurable quantities as
Note that
We will often use the parametrization
Figure 1. Qualitative behavior of
cosmological models in the
(
Qualitatively, the effect of a non-zero
Otherwise the universe recollapses. In particular, negative
For large, positive values of
where ``coss'' is defined as being cosh when
(see, e.g.
Börner &
Ehlers 1988).
Inequality 13 can be solved for zc, giving
where ``coss'' is as defined above. In general, such ``bounce''
cosmologies are ruled out by the mere existence of high redshift
quasars and (even more strongly) by the cosmic microwave background
(see Section 4.1).
First noted by
Lemaitre (1931),
so-called ``hesitating'' or ``loitering'' universes occur when
(cf Equations 12 and 14).
In view of the above arguments, and the observations described in
Section 4.1, it should be no surprise that
universes with large,
positive values for
Figure 2 shows the past and future expansion
history of the models
of Table 1, found by integrating
Equation 9. Model A shows the
familiar t2/3 expansion law. Nearly empty
(non-
Figure 2. Expansion history of the five
models A-E shown in Table 1 and
Figure 1.

 M and
M and

 here serve as constants
that parametrize the past
(or future) evolution in terms of quantities at the present epoch.
Equivalently, it was formerly common to parametrize the evolution by
here serve as constants
that parametrize the past
(or future) evolution in terms of quantities at the present epoch.
Equivalently, it was formerly common to parametrize the evolution by
 M (or
M (or
 0
0

 M/2) and the
deceleration parameter q0 = -
(R
M/2) and the
deceleration parameter q0 = -
(R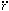 /
/
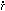 2)0.
Equation 9 then readily yields the relation
2)0.
Equation 9 then readily yields the relation

 M and
M and
 tot
tot

 M +
M +

 = 1 -
= 1 -
 k,
since it is
k,
since it is  tot < 1
(> 1) that makes the universe spatially open
(closed) - a fundamental issue in cosmology. For different assumed
values of
tot < 1
(> 1) that makes the universe spatially open
(closed) - a fundamental issue in cosmology. For different assumed
values of  M and
M and
 tot (or any other
parametrization) one gets
qualitatively different expansion histories.
Figure 1 displays the various regimes.
Felten & Isaacman
(1986)
show graphs of a(
tot (or any other
parametrization) one gets
qualitatively different expansion histories.
Figure 1 displays the various regimes.
Felten & Isaacman
(1986)
show graphs of a( ) for
various values of
) for
various values of  M
and
M
and 
 .
.

 M,
M,
 tot)
plane. Flat models, with
tot)
plane. Flat models, with
 tot = 1 and
non-zero
tot = 1 and
non-zero 
 , are on the vertical
line ACE. Models with
, are on the vertical
line ACE. Models with 
 = 0
lie on the diagonal line ABD. Use this
figure as a ``finding chart'' for
Figures 4,
7, and
9.
= 0
lie on the diagonal line ABD. Use this
figure as a ``finding chart'' for
Figures 4,
7, and
9.

 can be described as
follows: Looking from now towards the future, a positive value of
can be described as
follows: Looking from now towards the future, a positive value of
 (or
(or 
 ) tries to drive the
universe towards unbounded exponential
expansion - asymptotically becoming a DeSitter spacetime. It can fail
at this only if the matter density
) tries to drive the
universe towards unbounded exponential
expansion - asymptotically becoming a DeSitter spacetime. It can fail
at this only if the matter density
 M is so large as to
cause the
universe to recollapse before it reaches a sufficiently large size for
the
M is so large as to
cause the
universe to recollapse before it reaches a sufficiently large size for
the  -driven term (which
scales asymptotically as a2 in Equation 9) to
become significant - the narrow wedge in the upper-right corner of
Figure 1. A universe fated to recollapse has
some value a greater than
1 (the present value), such that the right hand side of Equation 9
vanishes. Some manipulation of the resulting cubic equations
(Glanfield 1966,
Felten & Isaacman
1986)
yields an analytic formula
for the boundary between recollapsing and perpetually expanding
universes in the
(
-driven term (which
scales asymptotically as a2 in Equation 9) to
become significant - the narrow wedge in the upper-right corner of
Figure 1. A universe fated to recollapse has
some value a greater than
1 (the present value), such that the right hand side of Equation 9
vanishes. Some manipulation of the resulting cubic equations
(Glanfield 1966,
Felten & Isaacman
1986)
yields an analytic formula
for the boundary between recollapsing and perpetually expanding
universes in the
( M,
M,

 ) plane (see
Figure 1):
Unbounded expansion occurs when
) plane (see
Figure 1):
Unbounded expansion occurs when


 implies
inevitable recollapse, even for spatially open universes, because the
effect of
implies
inevitable recollapse, even for spatially open universes, because the
effect of  is in the same
direction as gravity (attraction) rather than opposing it (repulsion).
is in the same
direction as gravity (attraction) rather than opposing it (repulsion).

 , the universe has a turning point
in its past, that is, it collapsed from infinite size to a finite
radius and is now reexpanding. This occurs when
, the universe has a turning point
in its past, that is, it collapsed from infinite size to a finite
radius and is now reexpanding. This occurs when

 M < 1/2 and cos when
M < 1/2 and cos when
 M >
1/2. (The join at
M >
1/2. (The join at  M
= 1/2 is perfectly analytic. The need for two
formulas to represent a single function is an artifact of solving
cubic equations. Here and below it is sometimes useful to use the
identities sinh-1x = ln[x +
(x2 + 1)1/2] and cosh-1 x
= ln[x + (x2 -
1)1/2].) The redshift zc of the ``bounce''
[which is the maximum redshift
of any object in the universe, since the universe never gets smaller
than a = (1 + zc)-1] satisfies
M
= 1/2 is perfectly analytic. The need for two
formulas to represent a single function is an artifact of solving
cubic equations. Here and below it is sometimes useful to use the
identities sinh-1x = ln[x +
(x2 + 1)1/2] and cosh-1 x
= ln[x + (x2 -
1)1/2].) The redshift zc of the ``bounce''
[which is the maximum redshift
of any object in the universe, since the universe never gets smaller
than a = (1 + zc)-1] satisfies

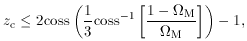

 is close to, but barely outside,
the bounce region of Equation 12. These are big-bang universes that
are now expanding, exponentially in fact, but formerly had an epoch of
indecision about whether to recollapse (from their matter content) or
to continue expanding (due to their large positive cosmological
constant). They thus spent a period of proper time loitering at a
nearly constant value of a. (The closer Equation 12 is to an equality,
the longer they coast.) The redshift of the loiter satisfies Equations
13 and 14 as equalities. This redshift is plotted in
Figure 1 as a
parameter along the loitering boundary. One sees that, analogously
with bouncing universes, a high redshift loiter requires unreasonably
small
is close to, but barely outside,
the bounce region of Equation 12. These are big-bang universes that
are now expanding, exponentially in fact, but formerly had an epoch of
indecision about whether to recollapse (from their matter content) or
to continue expanding (due to their large positive cosmological
constant). They thus spent a period of proper time loitering at a
nearly constant value of a. (The closer Equation 12 is to an equality,
the longer they coast.) The redshift of the loiter satisfies Equations
13 and 14 as equalities. This redshift is plotted in
Figure 1 as a
parameter along the loitering boundary. One sees that, analogously
with bouncing universes, a high redshift loiter requires unreasonably
small  M today. The
present value
M today. The
present value 
 in a universe that had a
loitering phase is related to zc (or
in a universe that had a
loitering phase is related to zc (or
 M) by
M) by


 are presently out of
fashion. We think they will remain so. Universes with
are presently out of
fashion. We think they will remain so. Universes with
 M > 1 are of course
out of fashion,
since all evidence is that there is a ``missing mass problem,'' and not
an ``excess mass problem.'' Our attention henceforth will therefore
focus on the ``fashionable'' region in
Figure 1, bounded approximately
by 0 <
M > 1 are of course
out of fashion,
since all evidence is that there is a ``missing mass problem,'' and not
an ``excess mass problem.'' Our attention henceforth will therefore
focus on the ``fashionable'' region in
Figure 1, bounded approximately
by 0 <  M < 1 and 0 <
M < 1 and 0 <
 tot < 1. In this
region the big questions are:
(a) Is
tot < 1. In this
region the big questions are:
(a) Is  tot
exactly equal to 1, as is required by inflationary
scenarios? And, (b) if it is equal to 1, is
tot
exactly equal to 1, as is required by inflationary
scenarios? And, (b) if it is equal to 1, is
 tot made of
tot made of
 M (cold
matter),
M (cold
matter), 
 (vacuum energy), or some
more exotic form of matter
(Peebles 1984,
M.S. Turner 1991)?
(vacuum energy), or some
more exotic form of matter
(Peebles 1984,
M.S. Turner 1991)?
 ) models B and D show
nearly identical histories, except close to a = 0 where B's larger
matter content has an effect. Models C and E - flat models with a
cosmological constant - have nearly identical future histories, since
both have already entered their exponential expansion phase. Model E,
being emptier of matter, shows a longer exponential phase to the past,
while C's matter content asserts itself more readily and drives the
expansion to a more recent big bang (a = 0).
) models B and D show
nearly identical histories, except close to a = 0 where B's larger
matter content has an effect. Models C and E - flat models with a
cosmological constant - have nearly identical future histories, since
both have already entered their exponential expansion phase. Model E,
being emptier of matter, shows a longer exponential phase to the past,
while C's matter content asserts itself more readily and drives the
expansion to a more recent big bang (a = 0).


 -dominated models like C
and E have already entered an
exponential expansion phase; also, they are older than the open
-dominated models like C
and E have already entered an
exponential expansion phase; also, they are older than the open

 = 0
models B and D.
= 0
models B and D.