


3.1 Type Ia supernovae
The most direct and theory-independent way to measure the cosmological
constant would be to actually determine the value of the scale factor
as a function of time. Unfortunately, the appearance of
 k
in formulae such as (42) renders this difficult.
Nevertheless, with sufficiently precise information about the
dependence of a distance measure on redshift we can disentangle
the effects of spatial curvature, matter, and vacuum energy, and
methods along these lines have been popular ways to try to constrain
the cosmological constant.
k
in formulae such as (42) renders this difficult.
Nevertheless, with sufficiently precise information about the
dependence of a distance measure on redshift we can disentangle
the effects of spatial curvature, matter, and vacuum energy, and
methods along these lines have been popular ways to try to constrain
the cosmological constant.
Astronomers measure distance in terms of the ``distance modulus'' m - M, where m is the apparent magnitude of the source and M its absolute magnitude. The distance modulus is related to the luminosity distance via
Of course, it is easy to measure the apparent magnitude, but
notoriously difficult to infer the absolute magnitude of a distant
object. Methods to estimate the relative absolute luminosities of
various kinds of objects (such as galaxies with certain characteristics)
have been pursued,
but most have been plagued by unknown evolutionary effects or
simply large random errors
[6].
Recently, significant progress has been made by using Type Ia
supernovae as ``standardizable candles''. Supernovae are rare -
perhaps a few per century in a Milky-Way-sized galaxy - but
modern telescopes allow observers to probe very deeply into
small regions of the sky, covering a very large number of galaxies
in a single observing run. Supernovae are also bright, and Type Ia's
in particular all seem to be of nearly uniform intrinsic luminosity
(absolute magnitude M ~ -19.5, typically comparable to the
brightness of the entire host galaxy in which they appear)
[36].
They
can therefore be detected at high redshifts (z ~ 1),
allowing in principle a good handle on cosmological effects
[37,
38].
The fact that all SNe Ia are of similar intrinsic luminosities fits
well with our understanding of these events as explosions which occur
when a white dwarf, onto which mass is gradually accreting from
a companion star, crosses the Chandrasekhar limit and explodes.
(It should be noted that our understanding of supernova
explosions is in a state of development, and theoretical models
are not yet able to accurately reproduce all of the important
features of the observed events. See
[39,
40,
41]
for some recent work.)
The Chandrasekhar limit is a nearly-universal quantity, so it is
not a surprise that the resulting explosions are of nearly-constant
luminosity. However, there is still a scatter of approximately
40% in the peak brightness observed in nearby supernovae, which
can presumably be traced to differences in the composition of the
white dwarf atmospheres. Even if we could collect enough data
that statistical errors could be reduced to a minimum, the existence
of such an uncertainty would cast doubt on any attempts to study
cosmology using SNe Ia as standard candles.
Fortunately, the observed differences
in peak luminosities of SNe Ia are very closely correlated with
observed differences in the shapes of their light curves:
dimmer SNe decline more rapidly after maximum brightness, while
brighter SNe decline more slowly
[42,
43,
44].
There is thus a one-parameter family of events, and measuring the
behavior of the light curve along with the apparent luminosity
allows us to largely correct for the intrinsic differences in
brightness, reducing the scatter from 40% to less than 15%
- sufficient precision to distinguish between cosmological models.
(It seems likely that the single parameter can be traced to the
amount of 56Ni produced in the supernova explosion; more
nickel implies both a higher peak luminosity and a higher
temperature and thus opacity, leading to a slower decline.
It would be an exaggeration, however, to claim that this behavior
is well-understood theoretically.)
Figure 3. Hubble diagram (distance modulus
vs. redshift) from the High-Z Supernova Team
[48].
The lines represent
predictions from the cosmological models with the specified
parameters. The lower plot indicates the difference between
observed distance modulus and that predicted in an open-universe model.
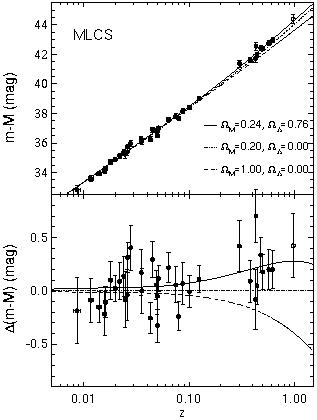
Figure 4. Hubble diagram from the Supernova
Cosmology Project
[52].
The bottom plot shows the number of standard
deviations of each point from the best-fit curve.
Following pioneering work reported in
[45],
two independent groups have undertaken searches for distant
supernovae in order to measure cosmological parameters.
Figure (3) shows the results for
m - M vs. z for
the High-Z Supernova Team
[46,
47,
48,
49]
and Figure (4)
shows the equivalent results for the Supernova Cosmology Project
[50,
51,
52].
Under the assumption that the energy density of the universe is
dominated by matter and vacuum components, these data can be
converted into limits on
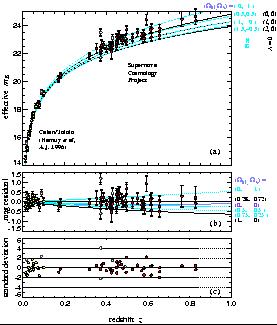
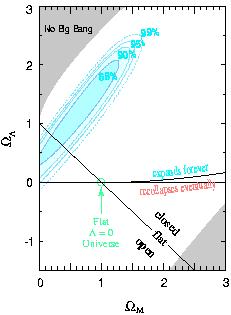
Figure 5. Constraints in the
Figure 6. Constraints in the
It is clear that the confidence intervals in the
Given the significance of these results, it is natural to
ask what level of confidence we should have in them.
There are a number of potential sources of systematic
error which have been considered by the two teams; see
the original papers
[47,
48,
52]
for a thorough discussion. The two most worrisome
possibilities are
intrinsic differences between Type Ia supernovae at high
and low redshifts
[53,
54]
possible extinction via intergalactic dust
[55,
56,
57,
58,
59].
(There is also the
fact that intervening weak lensing can change the
distance-magnitude relation, but this seems to be a small
effect in realistic universes
[60,
61].
Both effects have been carefully considered, and are thought
to be unimportant, although a better understanding will be
necessary to draw firm conclusions. Here, I will briefly
mention some of the relevant issues.
As thermonuclear explosions of white dwarfs, Type Ia supernovae
can occur in a wide variety of environments. Consequently, a
simple argument against evolution is that
the high-redshift environments, while chronologically younger,
should be a subset of all possible low-redshift environments,
which include regions that are ``young'' in terms of chemical
and stellar evolution. Nevertheless, even a small amount of
evolution could ruin our ability to reliably constrain
cosmological parameters
[53].
In their original papers
[47,
48,
52],
the supernova teams
found impressive consistency in the spectral and photometric
properties of Type Ia supernovae over a variety of redshifts
and environments (e.g., in elliptical vs. spiral
galaxies). More recently, however, Riess et al.
[54]
have presented tentative evidence for a
systematic difference in the properties of high- and low-redshift
supernovae, claiming that the risetimes (from initial explosion
to maximum brightness) were higher in the high-redshift
events. Apart from the issue of whether the existing data support
this finding, it is not immediately clear whether such a difference
is relevant to the distance determinations: first, because
the risetime is not used in
determining the absolute luminosity at peak brightness, and
second, because a process which only affects the very early
stages of the light curve is most plausibly traced to differences
in the outer layers of the progenitor, which may have a
negligible affect on the total energy output. Nevertheless,
any indication of evolution could bring into question the fundamental
assumptions behind the entire program. It is therefore essential
to improve the quality of both the data and the theories so that
these issues may be decisively settled.
Other than evolution, obscuration by dust is the leading concern
about the reliability of the supernova results. Ordinary
astrophysical dust does not obscure equally at all wavelengths,
but scatters blue light preferentially, leading to the
well-known phenomenon of ``reddening''. Spectral measurements
by the two supernova teams reveal a negligible amount of reddening,
implying that any hypothetical dust must be a novel ``grey''
variety. This possibility has been investigated by a number
of authors
[55,
56,
57,
58,
59].
These studies have found that even grey dust is highly constrained
by observations: first, it is likely to be intergalactic rather
than within galaxies, or it would lead to additional dispersion
in the magnitudes of the supernovae; and second, intergalactic dust
would absorb ultraviolet/optical radiation and re-emit it at
far infrared wavelengths, leading to stringent constraints from
observations of the cosmological far-infrared background.
Thus, while the possibility of obscuration has not been entirely
eliminated, it requires a novel kind of dust which is already
highly constrained (and may be convincingly ruled out by
further observations).
According to the best of our current understanding, then,
the supernova results indicating an accelerating universe seem
likely to be trustworthy. Needless to say, however, the possibility
of a heretofore neglected systematic effect looms menacingly
over these studies. Future experiments, including a proposed
satellite dedicated to supernova cosmology
[62], will both
help us improve our understanding of the physics of supernovae
and allow a determination of the distance/redshift relation to
sufficient precision to distinguish between the effects of a
cosmological constant and those of more mundane astrophysical
phenomena. In the meantime, it is important to obtain independent
corroboration using other methods.
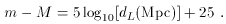
 M and
M and

 ,
as shown in Figures (5) and
(6).
,
as shown in Figures (5) and
(6).
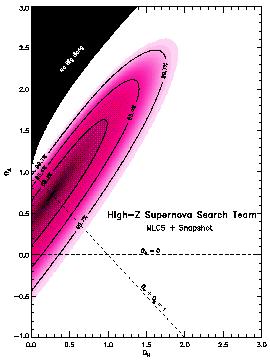
 M -
M -

 plane from the High-Z Supernova Team
[48].
plane from the High-Z Supernova Team
[48].
 M -
M -

 plane from the Supernova Cosmology Project
[52].
plane from the Supernova Cosmology Project
[52].
 M -
M -

 plane are consistent for
the
two groups, with somewhat tighter constraints obtained by the
Supernova Cosmology Project, who have more data points.
The surprising result is that both teams favor a positive
cosmological constant, and strongly rule out the traditional
(
plane are consistent for
the
two groups, with somewhat tighter constraints obtained by the
Supernova Cosmology Project, who have more data points.
The surprising result is that both teams favor a positive
cosmological constant, and strongly rule out the traditional
( M,
M,

 ) = (1,0) favorite universe.
They are even inconsistent with an open universe with zero
cosmological constant, given what we know about the matter
density of the universe (see below).
) = (1,0) favorite universe.
They are even inconsistent with an open universe with zero
cosmological constant, given what we know about the matter
density of the universe (see below).