


4.1 Supersymmetry
Although initially investigated for other reasons, supersymmetry
(SUSY) turns out to have a significant impact on the cosmological
constant problem, and may even be said to solve it halfway.
SUSY is a spacetime symmetry relating fermions and bosons to each
other. Just as ordinary symmetries are associated with
conserved charges, supersymmetry is associated with
``supercharges''
Q , where
, where
 is a spinor index (for introductions see
[131,
132,
133]).
As with ordinary symmetries, a theory may
be supersymmetric even though a given state is not supersymmetric;
a state which is annihilated by the supercharges,
Q
is a spinor index (for introductions see
[131,
132,
133]).
As with ordinary symmetries, a theory may
be supersymmetric even though a given state is not supersymmetric;
a state which is annihilated by the supercharges,
Q |
| > = 0, preserves supersymmetry,
while states with
Q
> = 0, preserves supersymmetry,
while states with
Q |
| >
>
 0 are said to spontaneously
break SUSY.
0 are said to spontaneously
break SUSY.
Let's begin by considering ``globally supersymmetric'' theories, which are defined in flat spacetime (obviously an inadequate setting in which to discuss the cosmological constant, but we have to start somewhere). Unlike most non-gravitational field theories, in supersymmetry the total energy of a state has an absolute meaning; the Hamiltonian is related to the supercharges in a straightforward way:
where braces represent the anticommutator. Thus, in a completely
supersymmetric state (in which
Q
where ðiW = ðW / ð
So the vacuum energy of a supersymmetric state in a globally
supersymmetric theory will vanish. This represents rather less
progress than it might appear at first sight, since: 1.) Supersymmetric
states manifest a degeneracy in the mass spectrum of bosons and
fermions, a feature not apparent in the observed world; and 2.)
The above results imply that non-supersymmetric states have a
positive-definite vacuum energy. Indeed, in a state where
SUSY was broken at an energy scale MSUSY, we would
expect a corresponding vacuum energy
Comparison of this discrepancy with the naive discrepancy
(54)
is the source of the claim that SUSY can solve the cosmological
constant problem halfway (at least on a log scale).
As mentioned, however, this analysis is strictly valid only
in flat space. In curved spacetime, the global transformations
of ordinary supersymmetry are promoted to the position-dependent
(gauge) transformations of supergravity. In this context the
Hamiltonian and supersymmetry generators play different
roles than in flat spacetime, but it is still possible to
express the vacuum energy in terms of a scalar field potential
V(
where DiW is the Kähler derivative,
Note that, if we take the canonical Kähler metric
Ki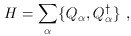
 |
| > = 0 for all
> = 0 for all
 ), the energy vanishes automatically,
<
), the energy vanishes automatically,
<  |H|
|H|
 > = 0
[134].
More concretely, in a given
supersymmetric theory we can explicitly calculate the contributions
to the energy from vacuum fluctuations and from the scalar potential
V. In the case of vacuum fluctuations, contributions
from bosons are exactly canceled by equal and opposite contributions
from fermions when supersymmetry is unbroken. Meanwhile,
the scalar-field potential in supersymmetric theories takes
on a special form; scalar fields
> = 0
[134].
More concretely, in a given
supersymmetric theory we can explicitly calculate the contributions
to the energy from vacuum fluctuations and from the scalar potential
V. In the case of vacuum fluctuations, contributions
from bosons are exactly canceled by equal and opposite contributions
from fermions when supersymmetry is unbroken. Meanwhile,
the scalar-field potential in supersymmetric theories takes
on a special form; scalar fields
 i must be complex
(to match the degrees of freedom of the fermions), and
the potential is derived from a function called the superpotential
W(
i must be complex
(to match the degrees of freedom of the fermions), and
the potential is derived from a function called the superpotential
W( i) which is
necessarily holomorphic (written in terms
of
i) which is
necessarily holomorphic (written in terms
of  i and not its complex
conjugate
i and not its complex
conjugate
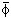 i). In
the simple Wess-Zumino
models of spin-0 and spin-1/2 fields, for example, the scalar
potential is given by
i). In
the simple Wess-Zumino
models of spin-0 and spin-1/2 fields, for example, the scalar
potential is given by
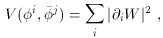
 i. In such a
theory, one can show that SUSY will be unbroken only for values
of
i. In such a
theory, one can show that SUSY will be unbroken only for values
of  i such that
ðiW = 0, implying
V(
i such that
ðiW = 0, implying
V( i,
i,
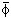 j) = 0.
j) = 0.

 ~
MSUSY4. In the real world, the fact that
accelerator experiments have not
discovered superpartners for the known particles of the Standard
Model implies that
MSUSY is of order 103 GeV or higher. Thus, we
are left with a discrepancy
~
MSUSY4. In the real world, the fact that
accelerator experiments have not
discovered superpartners for the known particles of the Standard
Model implies that
MSUSY is of order 103 GeV or higher. Thus, we
are left with a discrepancy
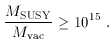
 i,
i,
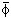 j).
In supergravity
V depends not only on the superpotential
W(
j).
In supergravity
V depends not only on the superpotential
W( i), but also on a
``Kähler potential''
K(
i), but also on a
``Kähler potential''
K( i,
i,
 j), and the
Kähler metric
Ki
j), and the
Kähler metric
Ki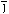 constructed from the Kähler potential by
Ki
constructed from the Kähler potential by
Ki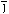 =
ð2 K
/ ð
=
ð2 K
/ ð i
ð
i
ð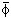 j.
(The basic role of the Kähler metric is to define the kinetic term
for the scalars, which takes the form
gµ
j.
(The basic role of the Kähler metric is to define the kinetic term
for the scalars, which takes the form
gµ Ki
Ki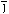 ðµ
ðµ
 i
ð
i
ð
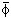 j.)
The scalar potential is
j.)
The scalar potential is
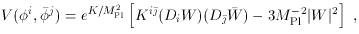
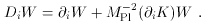
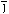 =
=
 i
i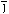 , in the limit
MPl
->
, in the limit
MPl
->  (G -> 0) the first term in
square brackets reduces to the flat-space
result (56). But with gravity, in addition to the
non-negative first term we find a second term
providing a non-positive contribution. Supersymmetry is
unbroken when DiW = 0; the effective
cosmological constant
is thus non-positive. We are therefore free to imagine a
scenario in which supersymmetry is broken in exactly the
right way, such that the two terms in parentheses cancel to
fantastic accuracy, but only at the cost of an
unexplained fine-tuning (see for example
[135]).
At the same time, supergravity is
not by itself a renormalizable quantum theory, and therefore
it may not be reasonable to hope that a solution can be
found purely within this context.
(G -> 0) the first term in
square brackets reduces to the flat-space
result (56). But with gravity, in addition to the
non-negative first term we find a second term
providing a non-positive contribution. Supersymmetry is
unbroken when DiW = 0; the effective
cosmological constant
is thus non-positive. We are therefore free to imagine a
scenario in which supersymmetry is broken in exactly the
right way, such that the two terms in parentheses cancel to
fantastic accuracy, but only at the cost of an
unexplained fine-tuning (see for example
[135]).
At the same time, supergravity is
not by itself a renormalizable quantum theory, and therefore
it may not be reasonable to hope that a solution can be
found purely within this context.